放物線・楕円・双曲線と領域：不等号の向きと最大・最小

二次曲線（放物線、楕円、双曲線）を利用して図を描くとき、不等号を用いるケースがあります。この場合、不等号の向きによって二次曲線で表される領域が異なります。

ただ二次関数に比べて、二次曲線の不等号が表す領域を理解するのは難しいです。楕円は例外的に容易に理解できるものの、放物線と双曲線について、不等号によって表される領域をどのように考えればいいのか理解する必要があります。

なお二次曲線と領域を学べば、二次曲線を用いる図形について、最大と最小を計算できるようになります。

それでは、どのように考えて二次曲線の領域を考えればいいのでしょうか。二次曲線での不等号の表す領域を解説していきます。

1 二次曲線と不等号の向きによる領域の違い
2 二次曲線での最大・最小の計算を行う
3 二次曲線で領域を答えられるようにする

二次曲線と不等号の向きによる領域の違い

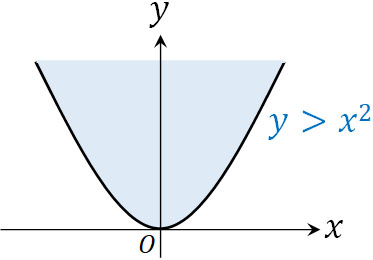
二次関数であれば、不等号を用いるとき、不等式が表す領域を理解しやすいです。例えば\(y>x^2\)であれば、下図のように、\(y=x^2\)で表される二次関数よりも\(y\)の値が大きい領域が該当します。

一方、二次曲線には以下の種類が存在します。

放物線
楕円
双曲線

それではこれらの二次曲線について、不等式によって表される領域はどのようになっているのでしょうか。

放物線での不等号と領域

まず、放物線での不等号と領域を考えましょう。放物線の方程式は\(y^2=4px\)です。

このとき、不等号の向きによって以下のように領域が変わります。

それでは、なぜこのようになるのでしょうか。二次関数というのは、放物線の特殊なパターンです。そこで、放物線の向きを以下のように変えましょう。

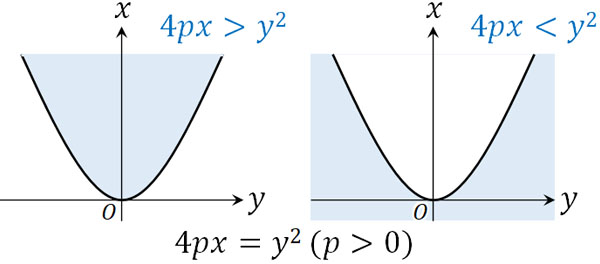
このように図を作り、二次関数のときと同様に考えると、なぜ先ほど記した図が成り立つのか理解できます。例えば\(4px>y^2\)の場合、\(4px=y^2\)によって記される曲線よりも、\(4px\)の値が大きければいいです。

放物線と二次関数は概念がほぼ同じです。そこで、放物線を二次関数と同じ形に変形することで不等式が表す領域を理解しましょう。

円を利用し、楕円の領域を学ぶ

楕円の特殊なケースが円です。そのため円で不等式を利用するとき、図形が表す領域を理解しているのであれば、楕円で不等式を利用する場合についても問題なく理解できます。円については、以下のように領域を考えます。

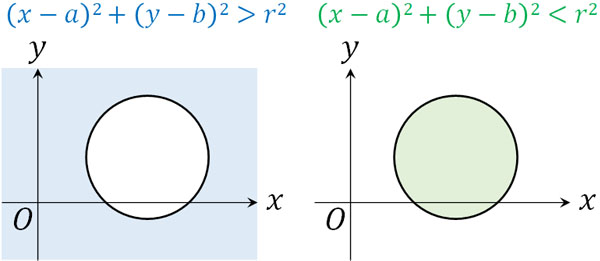
\(r\)は半径を表します。円の内部であれば、円の中心\((a,b)\)からの距離は\(r^2\)よりも値が小さくなります。そのため、上図の関係になります。

楕円についても、同様に考えましょう。以下のようになります。

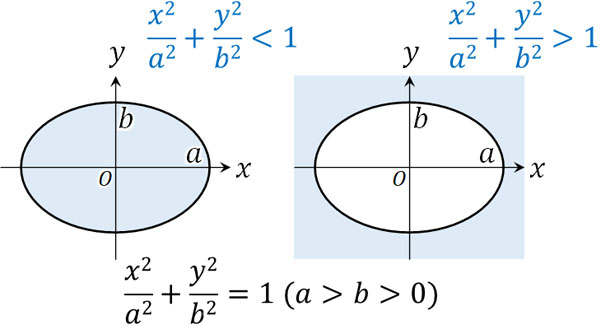
円のときと考え方は同じであるため、特に問題なく不等式が表す領域を理解できると思います。

双曲線では、わかりやすい点を確認する

一方、不等式が表す領域を理解しにくいのが双曲線です。双曲線では以下のように考えます。

どのように考えて、不等号が表す領域を判断すればいいのでしょうか。双曲線については、わかりやすい点（座標）を取ることで判断しましょう。例えば原点では\(x=0,y=0\)です。そのため双曲線の方程式に代入すると答えは0であり、明らかに1よりも低い値であるとわかります。

また\(x\)の値が非常に大きく、\(y=0\)の場合、答えは1よりも大きくなります。そのため、上図の関係が成り立ちます。特定の点について大小関係を考えることにより、双曲線での不等式の領域を判断できます。

二次曲線での最大・最小の計算を行う

それでは二次曲線に不等式が存在するとき、最大と最小の計算を行えるようになりましょう。以下の問題の答えは何でしょうか。

\(y≦x+1\)、\(\displaystyle\frac{x^2}{4}+y^2≦1\)を満たす実数\(x\)と\(y\)について、\(y-2x\)の最大値と最小値を求めましょう。

二次関数で不等式を学んでいるのであれば、同じ方法によって問題を解くことができます。\(y-2x=k\)とすると、\(y=2x+k\)です。そこで、切片\(k\)が最大または最小になるケースを確認しましょう。図を描くと以下のようになります。

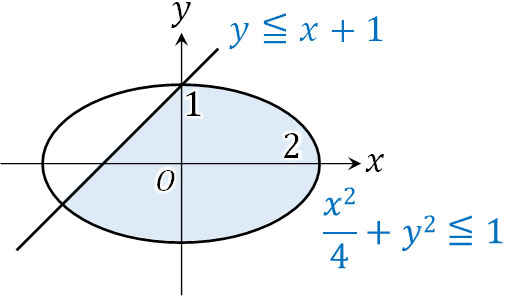
\(y=2x+k\)について、以下の場合では切片\(k\)が最大または最小になります。

\(y=2x+k\)が上図の左側にて楕円と直線の交点を通る場合、切片\(k\)は最大になります。一方、\(y=2x+k\)が楕円の右側で接する場合、切片\(k\)は最小になります。そこで、それぞれについて計算しましょう。

・最大値を求める

\(\displaystyle\frac{x^2}{4}+y^2=1\)は\(x^2+4y^2=4\)です。そこで、\(y=x+1\)を\(x^2+4y^2=4\)へ代入することで交点を計算しましょう。

\(x^2+4y^2=4\)

\(x^2+4(x+1)^2=4\)

\(5x^2+8x=0\)

\(x(5x+8)=0\)

こうして\(x=0,-\displaystyle\frac{8}{5}\)が答えです。なお図より、\(x=-\displaystyle\frac{8}{5}\)のときに\(k\)が最大になるとわかります。\(x=-\displaystyle\frac{8}{5}\)のとき、\(y=-\displaystyle\frac{3}{5}\)です。そこで、以下のように最大値を計算しましょう。

\(y-2x=k\)

\(-\displaystyle\frac{3}{5}+2×\displaystyle\frac{8}{5}=k\)

\(k=\displaystyle\frac{13}{5}\)

こうして、最大値は\(k=\displaystyle\frac{13}{5}\)とわかりました。

・最小値を求める

次に最小値を計算しましょう。楕円と\(y=2x+k\)が接するため、\(y=2x+k\)を\(x^2+4y^2=4\)へ代入しましょう。

\(x^2+4y^2=4\)

\(x^2+4(2x+k)^2=4\)

\(17x^2+16kx+4k^2-4=0\)

\(k\)の値が最小になるとき、直線と楕円は接します。つまり判別式\(D\)の値が0になるため、以下のように計算しましょう。

\(\displaystyle\frac{D}{4}=64k^2-17(4k^2-4)=0\)

\(-4k^2+68=0\)

\(k^2=17\)

\(k=±\sqrt{17}\)

つまり、\(k=\sqrt{17}\)または\(k=-\sqrt{17}\)のときに直線と楕円が接します。なお\(k=\sqrt{17}\)と\(k=-\sqrt{17}\)では、値は\(k=-\sqrt{17}\)で小さく、\(k=-\sqrt{17}\)が最小値になるとわかります。こうして、最大値だけでなく最小値を得ることができました。