ベクトルの内積：公式の意味、成分を利用しての長さ・面積の計算

ベクトルで重要な内容に内積があります。ベクトルには向きがあります。そのため、何も操作なしに2つのベクトルをかけてはいけません。ただ、同じ向きにそろえる場合は2つのベクトルをかけ算することができます。

ベクトルの向きをそろえるためには、角度を利用しなければいけません。cosθを利用し、ベクトルの向きを同じにした後にかけましょう。こうして、ベクトルの内積を計算できます。

特に物理では、ベクトルの向きをそろえる操作はひんぱんに利用されます。数学だけでなく、ほかの分野で利用されるのがベクトルの内積を計算するときの考え方です。ベクトルの内積を計算できない場合、力学の問題を解くことはできません。

それでは、どのようにベクトルの向きをそろえればいいのでしょうか。また、どのようにベクトルのかけ算をすればいいのでしょうか。ベクトルの内積を計算する方法を解説していきます。

1 角度を考慮したベクトルの大きさ
- 1.1 ベクトルの内積を利用し、角度（なす角）を得る
- 1.2 平行と垂直でのベクトルの内積
2 内積の性質を利用して計算する
- 2.1 内積を利用するベクトルの大きさと最小値の計算
- 2.2 内積と三角形の面積の計算：公式とsinθの利用
3 内積を利用して長さや角度、面積を得る

角度を考慮したベクトルの大きさ

向きが存在しない場合、数字同士をかけ算することができます。一方で向きをもつ場合、何も考えずにかけ算をしてはいけません。かけ算が可能なのは、向きが同じ（または反対）であるときです。

そこで、向きを同じにしましょう。例えば以下のように\(\overrightarrow{a}\)がある場合、\(x\)成分と\(y\)成分の大きさはいくらでしょうか。

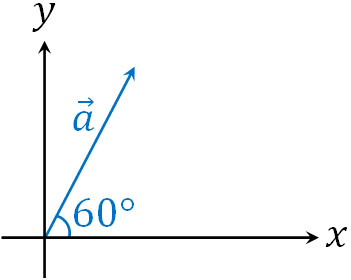
この場合、以下のように計算できます。

\(x\)成分：\(|\overrightarrow{a}|cos60°=\displaystyle\frac{|\overrightarrow{a}|}{2}\)
\(y\)成分：\(|\overrightarrow{a}|sin60°=\displaystyle\frac{\sqrt{3}|\overrightarrow{a}|}{2}\)

\(|\overrightarrow{a}|\)は\(\overrightarrow{a}\)の大きさ（ベクトルの長さ）を表します。そこで角度を利用することにより、\(x\)成分や\(y\)成分の大きさがわかります。

この計算方法を利用して、2つのベクトルの向きを同じにしましょう。向きが異なる場合、2つのベクトルをかけることができません。そこで向きを同じにすることにより、かけ算できるようにするのです。例えば以下の場合、2つのベクトルのかけ算を以下のように表すことができます。

\(\overrightarrow{a}·\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cosθ\)

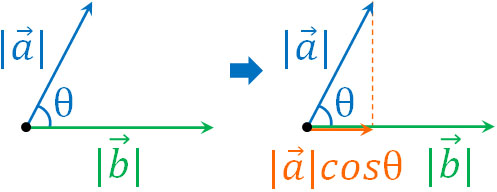
これがベクトルの内積です。「ベクトルの向きを同じにした後、かけ算することでベクトルの内積になる」と定義します。

なお、この公式を覚えてはいけません。図形によってはcosθではなく、sinθを利用することでベクトルの向きを同じにするケースもあるからです。つまり、公式を暗記しても意味がありません。

そこで、角度を利用してベクトルの向きをそろえることにより、かけ算できるようになることを学びましょう。そうすれば、公式なしにベクトルの内積を計算できるようになります。

ベクトルの内積を利用し、角度（なす角）を得る

先ほど、図形を利用してベクトルの内積を定義しました。角度を利用してベクトルの向きをそろえることにより、かけ算することができます。

なおベクトルの内積では、もう一つの定義があります。\(\overrightarrow{a}=(a_1,a_2)\)、\(\overrightarrow{b}=(b_1,b_2)\)とするとき、代数学（文字を用いる数学）では、以下のようにベクトルの内積を定義します。

\(\overrightarrow{a}·\overrightarrow{b}=a_1b_1+a_2b_2\)

詳細は解説しませんが、余弦定理と\(\overrightarrow{a}·\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cosθ\)を利用することにより、この公式を導出できます。重要なのは、2つのベクトル成分がわかれば内積を計算できることにあります。

また\(\overrightarrow{a}·\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cosθ\)であるため、以下のように式を変形できます。

\(cosθ=\displaystyle\frac{\overrightarrow{a}·\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}\)

そのため、2つのベクトル成分がわかればなす角を得ることもできます。それでは、以下の問題の答えは何でしょうか。

\(\overrightarrow{a}=(1,3)\)、\(\overrightarrow{b}=(2,1)\)のとき、2つのベクトルの内積となす角を求めましょう。

先ほど解説した公式を利用することにより、2つのベクトルの内積を以下のように計算できます。

\(\overrightarrow{a}·\overrightarrow{b}=1×2+3×1=5\)

ベクトルの内積を計算できたため、次に2つのベクトルによって作られる角度を計算しましょう。なお、\(\overrightarrow{a}\)と\(\overrightarrow{b}\)の長さは以下のようになります。

\(|\overrightarrow{a}|=\sqrt{1^2+3^2}=\sqrt{10}\)
\(|\overrightarrow{b}|=\sqrt{2^2+1^2}=\sqrt{5}\)

そこで、以下のように計算しましょう。

\(\overrightarrow{a}·\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cosθ\)

\(5=\sqrt{10}×\sqrt{5}×cosθ\)

\(cosθ=\displaystyle\frac{1}{\sqrt{2}}\)

\(cosθ=\displaystyle\frac{1}{\sqrt{2}}\)となるため、\(θ=45°\)です。こうして、2つのベクトルのなす角を計算することができました。

平行と垂直でのベクトルの内積

次に、2つのベクトルが平行なとき、ベクトルの内積を計算できるようになりましょう。2つのベクトルが平行というのは、\(θ=0°\)であることを意味します。\(cos0°=1\)であるため、2つのベクトルが平行だと以下の関係が成り立ちます。

\(\overrightarrow{a}·\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|\)

なお、2つのベクトルが反対向きであるケースもあります。そのため、以下の関係が成り立つ場合も2つのベクトルは平行です。

\(\overrightarrow{a}·\overrightarrow{b}=-|\overrightarrow{a}||\overrightarrow{b}|\)

それでは、2つのベクトルが垂直の場合はどのようになるのでしょうか。垂直だと、ベクトルのなす角は90°です。

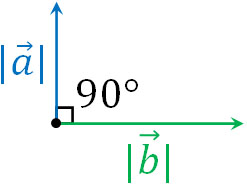
\(cos90°=0\)です。そのため、ベクトルの内積は必ず0になります。

\(\overrightarrow{a}·\overrightarrow{b}=0\)

ベクトルの内積で角度を利用することを理解すれば、2つのベクトルが平行や垂直のとき、なぜ上記の公式が成り立つのかわかります。

内積の性質を利用して計算する

それでは、内積の性質を利用して計算できるようになりましょう。内積の計算では、以下の性質があります。

交換法則：\(\overrightarrow{a}·\overrightarrow{b}=\overrightarrow{b}·\overrightarrow{a}\)
分配法則：\(\overrightarrow{a}(\overrightarrow{b}+\overrightarrow{c})=\overrightarrow{a}·\overrightarrow{b}\)\(+\overrightarrow{a}·\overrightarrow{c}\)
実数倍：\(k\overrightarrow{a}(\overrightarrow{b})=\overrightarrow{a}(k\overrightarrow{b})\)\(=k(\overrightarrow{a}·\overrightarrow{b})\)

これらの内容については、問題なく理解できると思います。なお内積の計算で重要なのは、以下の公式が成り立つことです。

\(\overrightarrow{a}·\overrightarrow{a}=|\overrightarrow{a}|^2\)

数学でベクトルの内積を計算するとき、この関係を利用することは多いです。\(\overrightarrow{a}\)が2つある場合、当然ながら平行です。\(cos0°=1\)であるため、\(\overrightarrow{a}·\overrightarrow{a}=|\overrightarrow{a}||\overrightarrow{a}|\)となり、先ほどの公式が成り立ちます。

参考までに、\(\overrightarrow{a}≧0\)であるため\(|\overrightarrow{a}|=\sqrt{\overrightarrow{a}·\overrightarrow{a}}\)が成り立ちます。それでは、ここまでの知識をもとにして練習問題を解きましょう。以下の問題の答えは何でしょうか。

\(|\overrightarrow{a}|=2\)、\(|\overrightarrow{b}|=1\)であり、\(\overrightarrow{a}-\overrightarrow{b}\)と\(2\overrightarrow{a}+5\overrightarrow{b}\)が垂直のとき、\(\overrightarrow{a}\)と\(\overrightarrow{b}\)によるなす角を求めましょう。

\(\overrightarrow{a}-\overrightarrow{b}\)と\(2\overrightarrow{a}+5\overrightarrow{b}\)が垂直であるため、以下の式を作りましょう。

\((\overrightarrow{a}-\overrightarrow{b})(2\overrightarrow{a}+5\overrightarrow{b})=0\)

\(2|\overrightarrow{a}|^2+3\overrightarrow{a}·\overrightarrow{b}-5|\overrightarrow{b}|^2=0\)

\(8+3\overrightarrow{a}·\overrightarrow{b}-5=0\)

\(3\overrightarrow{a}·\overrightarrow{b}=-3\)

\(\overrightarrow{a}·\overrightarrow{b}=-1\)

次に、ベクトルの内積を計算する公式を利用して2つのベクトルのなす角を計算しましょう。

\(\overrightarrow{a}·\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cosθ\)

\(-1=2×1×cosθ\)

\(cosθ=-\displaystyle\frac{1}{2}\)

\(cosθ=-\displaystyle\frac{1}{2}\)であるため、\(θ=120°\)とわかります。こうして、2つのベクトルのなす角を計算することができました。

内積を利用するベクトルの大きさと最小値の計算

数学の計算では、最大値や最小値を求める問題がひんぱんに出題されます。そこでベクトルが関わる計算についても、最小値を計算できるようになりましょう。

ベクトルの大きさ（ベクトルの長さ）に関する計算問題では、二乗することで問題を解くことを考えましょう。二乗によって\(\overrightarrow{a}·\overrightarrow{b}\)を得ることができたり、二次関数を作れたりするのです。

それでは、以下の問題の答えは何でしょうか。

\(|\overrightarrow{a}|=2\)、\(|\overrightarrow{b}|=3\)、\(|\overrightarrow{a}+\overrightarrow{b}|=1\)のとき、\(|\overrightarrow{a}+t\overrightarrow{b}|\)の最小値を求めましょう。

まず、\(\overrightarrow{a}\)と\(\overrightarrow{b}\)の内積を計算します。前述の通り、二乗することを考えましょう。\(|\overrightarrow{a}+\overrightarrow{b}|=1\)を二乗することにより、\(\overrightarrow{a}·\overrightarrow{b}\)を得られます。

\(|\overrightarrow{a}+\overrightarrow{b}|^2=1^2\)

\(|\overrightarrow{a}|^2+2\overrightarrow{a}·\overrightarrow{b}+|\overrightarrow{b}|^2=1\)

\(4+2\overrightarrow{a}·\overrightarrow{b}+9=1\)

\(2\overrightarrow{a}·\overrightarrow{b}=-12\)

\(\overrightarrow{a}·\overrightarrow{b}=-6\)

こうして、ベクトルの内積は\(\overrightarrow{a}·\overrightarrow{b}=-6\)とわかりました。

次に、\(|\overrightarrow{a}+t\overrightarrow{b}|\)を二乗しましょう。二乗して最小値になる値を見つければ、二乗しない場合についても最小になります。そこで、以下のように計算しましょう。

\(|\overrightarrow{a}+t\overrightarrow{b}|^2\)

\(=|\overrightarrow{a}|^2+2t\overrightarrow{a}·\overrightarrow{b}+t^2|\overrightarrow{b}|^2\)

\(=4+2t×(-6)+t^2×9\)

\(=9t^2-12t+4\)

\(=9\left(t^2-\displaystyle\frac{4}{3}t\right)+4\)

\(=9\left(t-\displaystyle\frac{2}{3}\right)^2\)

こうして\(t=\displaystyle\frac{2}{3}\)のとき、\(|\overrightarrow{a}+t\overrightarrow{b}|^2\)は最小値0となります。そのため、二乗しない場合も最小値は0です。

内積と三角形の面積の計算：公式とsinθの利用

ベクトルを利用することにより、三角形の面積を計算することもできます。三角形の面積を得る公式として以下があります。

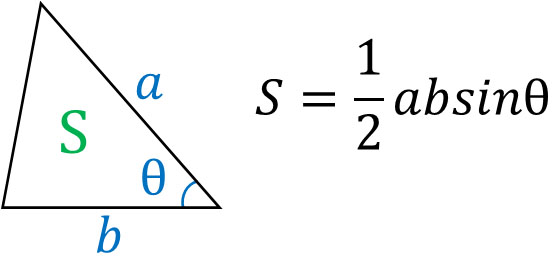
この公式は既に学んでいると思います。公式を覚える必要はありません。たてと横をかけた後、半分にすることで三角形の面積を得られることを知っていれば、この公式を導出できます。\(a·sinθ\)はたての長さを表すからです。

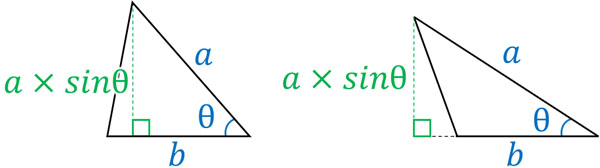
ベクトルでは、\(|\overrightarrow{a}|\)や\(|\overrightarrow{a}|\)は長さを表します。また、2つのベクトルを利用することによってcosθを得ることができます。そのため、\(sin^2θ+cos^2θ=1\)を利用することにより、sinθを得られます。こうして、三角形の面積を計算できるのです。

それでは、以下の問題を解いてみましょう。