座標を表すとき、通常は\(x\)軸と\(y\)軸を利用します。ただ点の座標を示すとき、原点との距離\(r\)と\(x\)軸との角度\(θ\)を用いて表すことも可能です。
\(r\)と\(θ\)を用いて表される座標を極座標といいます。また、極座標を用いて表す方程式を極方程式といいます。
極方程式を用いて直線や円を表すとき、複数の方法があります。極方程式を覚えても意味がないので、どのように極方程式を作ればいいのか理解しましょう。また極方程式の作り方を知れば、二次曲線(放物線、楕円、双曲線)の極方程式を得ることもできます。
それでは、極座標や極方程式を利用してどのように距離や面積を計算すればいいのでしょうか。公式の利用法や極方程式の導出法を解説していきます。
もくじ
距離と角度を用いて表す極座標
座標を用いることにより、平面上の一つの点を表すことができます。一方、原点からの距離と角度を用いて一つの点を表すこともできます。
例えば点Pが\((4,4)\)の場合、原点からの長さは\(4\sqrt{2}\)であり、角度は\(\displaystyle\frac{π}{4}\)です。そのため、長さと角度を用いて点Pを表すことができます。極座標は\((r,θ)\)で表すため、\((4,4)\)は\(\left(4\sqrt{2},\displaystyle\frac{π}{4}\right)\)と表せます。
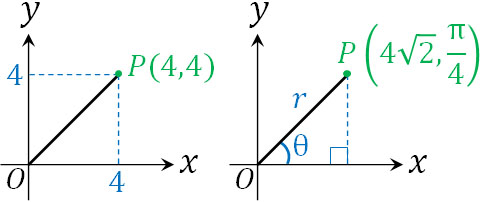
このとき、\((x,y)\)は以下のように表すことができます。
- \(x=rcosθ\)
- \(y=rsinθ\)
また、\((x,y)\)を用いて以下のように\(r\)と\(θ\)を計算できます。
- \(r=\sqrt{x^2+y^2}\)
- \(cosθ=\displaystyle\frac{x}{r}\)、\(sinθ=\displaystyle\frac{y}{r}\)
これらの関係については、説明しなくても理解できると思います。
2点間の距離の長さと面積の計算
それでは、極座標を用いて2点間の距離を計算できるようになりましょう。方法は簡単であり、余弦定理を利用します。
点Oを極(原点)とすると、点A\((r_1,θ_1)\)と点B\((r_2,θ_2)\)の距離ABを以下のように表すことができます。
- \(AB=\sqrt{r_1^2+r_2^2-2r_1r_2cos(θ_2-θ_1)}\)
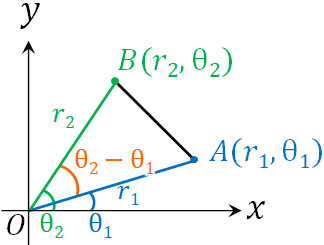
余弦定理を利用して式を表しているだけなので、特に問題なく理解できると思います。余弦定理を利用して計算すればいいと学べば、新たに公式を覚えなくてもいいとわかります。
また、極方程式を利用して面積を計算することもできます。面積\(S\)を得る公式を覚える必要もなく、\(S=\displaystyle\frac{1}{2}absinθ\)を利用して計算しましょう。
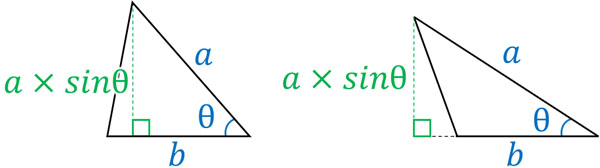
先ほどと同じく、点A\((r_1,θ_1)\)と点B\((r_2,θ_2)\)を利用すると、面積の公式は以下のようになります。
- \(S=\displaystyle\frac{1}{2}r_1r_2|sin(θ_2-θ_1)|\)
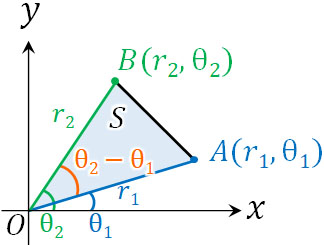
三角形の面積を計算するときについても、公式を覚えることなく、極座標を利用して面積を得ましょう。
極方程式を利用して直線と円を表現する
それでは、極座標を用いて直線や円を表現しましょう。極座標を用いて表す直線や円の式を極方程式といいます。
極方程式についても、極座標と同様に暗記してはいけません。教科書に記載されている極方程式を覚えても意味がないため、直線の極方程式や円の極方程式を得る方法を学ぶ必要があります。
なお、極方程式の公式を見ても理解できません。そこで、図を利用しましょう。図を描けば、なぜそのような極方程式になるのか容易にわかります。
図を用いて直線の極方程式を表す
極座標を用いて直線を表すとき、2つの方法があります。以下が直線の極方程式です。
- 極Oを通り、始線とのなす角が\(α\)の場合:\(θ=α\)
- 点A\((a,α)\)を通り、OAに垂直な直線:\(rcos(θ-α)=a\)
恐らく意味を理解できないと思うので、この極方程式が何を意味しているのか学びましょう。
・極Oを通り、始線とのなす角が\(α\)の場合:\(θ=α\)
例として、始線とのなす角が\(\displaystyle\frac{π}{4}\)のケースを考えましょう。角度は\(\displaystyle\frac{π}{4}\)であるものの、長さ\(r\)が決まっていない場合、角度が\(\displaystyle\frac{π}{4}\)で極Oを通る直線となります。
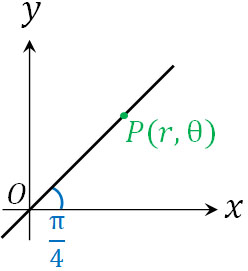
そのため、直線の極方程式は\(θ=α\)となるのです。
・点A\((a,α)\)を通り、OAに垂直な直線:\(rcos(θ-α)=a\)
点A\((a,α)\)を通る場合、角度\(θ\)によって点Pの場所が変化します。一方、極Oと点Aの距離は変化しません。そこで、OAの長さを式で表しましょう。図を作ると、以下の関係が成り立つとわかります。
- \(OA=OPcos∠POA\)
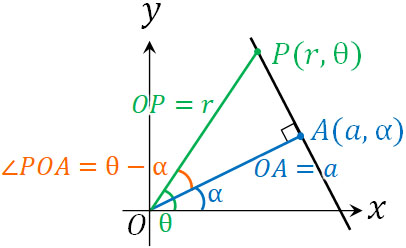
\(OA=a\)、\(OP=r\)、\(∠POA=θ-α\)です。そのため、以下の方程式が成り立つとわかります。
- \(rcos(θ-α)=a\)
教科書に記載されている極方程式を見ても理解できないものの、図を利用すれば容易に極方程式を作れるようになります。
円の極方程式:中心と半径の関係
次に、円の極方程式を確認しましょう。以下が円の極方程式です。
- 中心が極O、半径\(a\)の円:\(r=a\)
- 中心\((a,0)\)、半径\(a\)の円:\(r=2acosθ\)
- 中心\((r_0,θ_0)\)、半径\(a\)の円:\(r^2-2rr_0cos(θ-θ_0)\)\(+r_0^2\)\(=a^2\)
それぞれの極方程式が何を表すのか確認しましょう。
・中心が極O、半径\(a\)の円:\(r=a\)
中心が極Oの場合、半径\(a\)はOPの長さ\(r\)となります。そのため、\(r=a\)が成り立ちます。
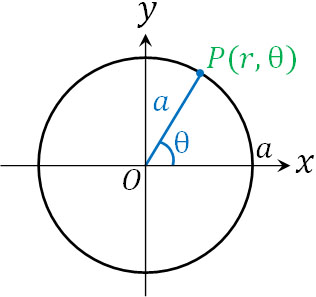
・中心\((a,0)\)、半径\(a\)の円:\(r=2acosθ\)
中心\((a,0)\)、半径\(a\)の円はどのように表せばいいでしょうか。以下の図を作りましょう。
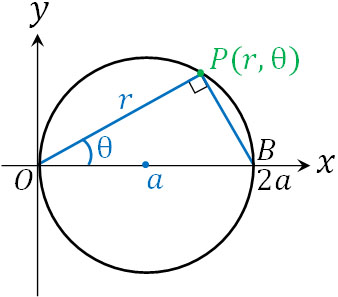
この図を作ると、以下の式を作れます。
\(OP=OCcos∠BOP\)
\(r=2acosθ\)
これが、円の極方程式です。辺の長さと角度を利用することにより、極方程式で表すことができます。
・中心\((r_0,θ_0)\)、半径\(a\)の円:\(r^2-2rr_0cos(θ-θ_0)\)\(+r_0^2\)\(=a^2\)
ただ、円の中心が極Oや始線上に存在しないケースが多いです。そこで中心\((r_0,θ_0)\)、半径\(a\)の円を極方程式で表せるようになりましょう。
先ほど、2点間の距離を極座標で表すときに余弦定理を利用しました。円を極方程式で表すときについても、余弦定理を利用して計算しましょう。まず、以下の図を作ります。
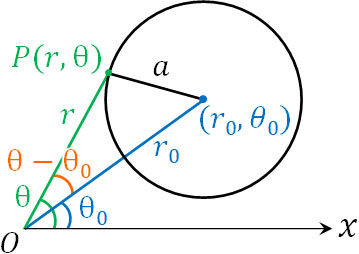
余弦定理を利用すると、以下の式を作れます。
- \(a^2=r^2+r_0^2-2rr_0cos(θ-θ_0)\)
こうして、先ほど記した式を作ることができました。余弦定理を利用すればいいと学べば、円の極方程式を覚える必要がないとわかります。
極方程式を直交座標の方程式で表す
極座標に対して、\(x\)座標と\(y\)座標を用いて表す方法を直交座標といいます。私たちがこれまで学んできた図形は直交座標を用いていたのです。それでは極方程式について、直交座標での方程式で表せるようにしましょう。
復習すると、以下の関係が成り立ちます。
- \(r^2=x^2+y^2\)
- \(cosθ=\displaystyle\frac{x}{r}\)、\(sinθ=\displaystyle\frac{y}{r}\)
そこで、この関係を利用することによって式を変形しましょう。以下の極方程式について、直交座標の方程式で表すとどのようになるでしょうか。
- \(r=\sqrt{3}cosθ+sinθ\)
両辺に\(r\)をかけた後、\(r^2=x^2+y^2\)を代入しましょう。
\(r=\sqrt{3}cosθ+sinθ\)
\(r^2=\sqrt{3}rcosθ+rsinθ\)
\(x^2+y^2=\sqrt{3}rcosθ+rsinθ\)
また\(cosθ=\displaystyle\frac{x}{r}\)、\(sinθ=\displaystyle\frac{y}{r}\)より、\(x=rcosθ\)、\(y=rsinθ\)となります。そこで、この式を代入しましょう。
\(x^2+y^2=\sqrt{3}rcosθ+rsinθ\)
\(x^2+y^2=\sqrt{3}x+y\)
\(x^2-\sqrt{3}x+y^2-y=0\)
\(\left(x-\displaystyle\frac{\sqrt{3}}{2}\right)^2+\left(y-\displaystyle\frac{1}{2}\right)^2=1\)
こうして、円の方程式を得ることができました。
ちなみに、直交座標の方程式を極方程式へ変換するとき、\(x=rcosθ\)と\(y=rsinθ\)を利用して代入しましょう。
離心率を利用し、二次曲線の極方程式を表す
それでは、二次曲線(放物線、楕円、双曲線)を極方程式で表すとどのようになるのでしょうか。原点Oが焦点の一つであり、準線が\(x=-a\)のとき、点P\((r,θ)\)をどのように表せばいいでしょうか。点Pから準線へ垂直に線を引くときの交点をH、離心率を\(e\)とすると以下の図を描けます。
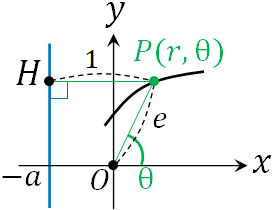
\(OP=r\)であり、\(HP=a+rcosθ\)です。また、離心率を用いて以下の式を作りましょう。
\(1:e=HP:OP\)
\(eHP=OP\)
\(e(a+rcosθ)=r\)
\(ea+ercosθ=r\)
\(r(1-ecosθ)=ea\)
\(r=\displaystyle\frac{ea}{1-ecosθ}\)
こうして、二次曲線の極方程式を表すことができました。
なお先ほど、準線が焦点(極)の左側に存在する場合を想定して極方程式を作りました。一方で準線が焦点(極)の右側に存在する場合、極方程式は\(r=\displaystyle\frac{ea}{1+ecosθ}\)となります。
離心率\(e\)によって、二次曲線は以下のように変化します。
- \(0<e<1\):楕円
- \(e=1\):放物線
- \(e>1\):双曲線
極方程式では、すべての二次曲線を一つの式で表すことができます。この点について、極方程式は便利です。
極座標・極方程式を用いて点を表す
私たちが日常的に利用する平面図形の概念が直交座標です。一方で極座標では、極(原点)から点までの長さ\(r\)と角度\(θ\)を利用して表します。なお極座標を用いて2点間の距離や面積を計算するとき、公式を覚えるのではなく、計算方法を理解しましょう。
極座標を用いて直線や円を表す場合、極方程式と呼ばれます。極方程式を覚えても意味がないため、図を利用して極方程式を作れるようになりましょう。そうすれば覚える必要がないですし、すべての応用問題に対処できます。
なお極方程式を利用することにより、二次曲線(放物線、楕円、双曲線)を表すこともできます。準線の位置によって極方程式は異なるものの、一つの式によってすべての二次曲線を表すことができます。
直交座標だけでなく、極座標を用いて点を表せるようになりましょう。また図を描くことにより、極方程式を導出できるようになりましょう。






