私たちが計算問題を解くとき、多くは一次方程式や二次方程式を利用します。ただ場合によっては、三次方程式や四次方程式を解かなければいけないことがあります。三次方程式では3つの解があり、四次方程式では4つの解があります。
三次以上の方程式を高次方程式といいます。高次方程式を解くとき、公式の利用や因数定理の活用など、解き方を学びましょう。
なお高次方程式では、次数を下げたり、二重解をもつ場合の計算をしたりと独自の問題が出題されます。また、三次方程式での解と係数の関係も学ばなければいけません。
高次方程式では問題の解き方が複雑になります。そこで、どのように高次方程式の計算をすればいいのか解説していきます。
もくじ
高次方程式を解く方法は主に3つ
三次方程式や四次方程式など、高次方程式を解く方法は主に3つあります。以下の方法です。
- 公式(因数分解、解の公式)を利用して計算する
- 文字の置き換えをして計算する
- 因数定理を利用して因数分解する
それぞれの方法を確認しましょう。
公式を利用して解を得る
最もわかりやすい方法が公式の利用です。まず、公式を利用することで因数分解しましょう。その後、解の公式を利用することで解を得ます。それでは、以下の式の答えは何でしょうか。
- \(x^3=8\)
まず、因数分解をしましょう。以下のように計算します。
\(x^3=8\)
\(x^3-8=0\)
\(x^3-2^3=0\)
\((x-2)(x^2+2x+4)=0\)
こうして、\(x=2\)が答えとわかります。なお三次方程式であるため、答えは3つあります。そこで、解の公式を利用して\(x^2+2x+4=0\)の答えを得ましょう。
\(x=\displaystyle\frac{-2±\sqrt{2^2-4×4}}{2}\)
\(x=\displaystyle\frac{-2±\sqrt{12}i}{2}\)
\(x=-1±\sqrt{3}i\)
こうして、答えは\(x=2\)と\(x=-1±\sqrt{3}i\)になるとわかりました。
置き換えによって計算する
文字の置き換えをすることによって高次方程式を解けることもあります。文字の置き換えを行い、因数分解と解の公式を利用することで答えを得るのです。例題として、以下の問題を解きましょう。
- \(x^4+2x^2-3=0\)
\(x^2=X\)としましょう。このように置き換えることにより、式は\(X^2+2X-3=0\)となるので因数分解できます。
\(X^2+2X-3=0\)
\((X+3)(X-1)=0\)
\(X=1,-3\)が答えです。そこで、置き換えた文字を戻して計算しましょう。
・\(x^2=1(X=1)\)の計算
\(x^2=1\)
\(x=±1\)
・\(x^2=-3(X=-3)\)の計算
\(x^2=-3\)
\(x=±\sqrt{3}i\)
こうして、答えは\(x=±1\)と\(x=±\sqrt{3}i\)であるとわかりました。
因数定理を利用し、因数分解をする
どのように因数分解すればいいのかわからない場合、因数定理を利用して因数分解しましょう。ヒントなしに因数分解するのは難しいものの、因数定理を利用すれば因数を見つけやすくなります。
\(x\)に値を代入し、答えが0になれば、因数を見つけることができます。例えば\(P(1)=0\)の場合、\(x=1\)で答えが0になるため、\(P(x)\)は\(x-1\)を因数にもつとわかります。それでは、次の問題を解きましょう。
- \(x^3+3x^2+4x+4=0\)
\(P(x)=x^3+3x^2+4x+4\)とすると、\(x\)に何の値を代入すると答えが0になるでしょうか。ランダムに値を代入すると、\(x=-2\)のときに\(P(-2)=0\)になるとわかります。つまり、\(P(x)\)は\(x+2\)を因数にもつとわかります。
そこで、以下のように割り算をしましょう。
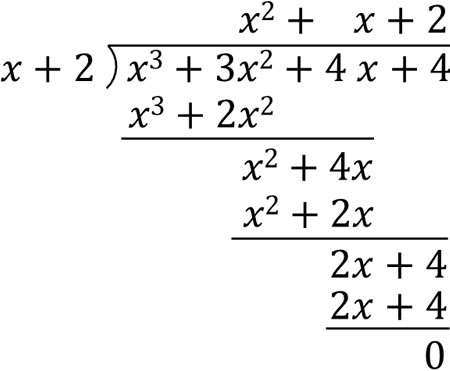
こうして、\(P(x)=x^3+3x^2+4x+4\)を以下のように因数分解できるとわかります。
- \(P(x)=(x+2)(x^2+x+2)\)
\(x^3+3x^2+4x+4=0\)について、解の一つは\(x=-2\)です。次に、\(x^2+x+2=0\)となる解を計算しましょう。解の公式より、以下のように答えを得られます。
\(x=\displaystyle\frac{-1±\sqrt{7}i}{2}\)
こうして、答えは\(x=-2\)と\(x=\displaystyle\frac{-1±\sqrt{7}i}{2}\)であるとわかりました。
置き換えや因数定理を行えない場合の計算方法
なお場合によっては、置き換えや因数定理を利用できないケースもあります。この場合、平方の差に着目しましょう。つまり、無理やり二乗の形を作るのです。例題として、以下の問題を解きましょう。
- \(x^4+x^2+4=0\)
この式では、文字の置き換えをしても、因数定理を利用しても問題を解けません。そこで、二乗の形を作りましょう。式を確認すると、\((x^2+2)^2\)であれば、似た式を作れるとわかります。
ただ、つじつまを合わせる必要があります。\((x^2+2)^2=x^4+4x^2+4\)であるため、元の式よりも\(3x^2\)が多いです。そこで、\(3x^2\)を引きましょう。つまり、以下の式を作ります。
\((x^2+2)^2-3x^2=0\)
こうして、\(x^4+x^2+4=0\)を\((x^2+2)^2-3x^2=0\)へ変形することができました。このように式を変形すると、因数分解することができます。\(a^2-b^2=(a+b)(a-b)\)であるため、以下のように因数分解しましょう。
\((x^2+2)^2-3x^2=0\)
\((x^2+2+\sqrt{3}x)(x^2+2-\sqrt{3}x)=0\)
\((x^2+\sqrt{3}x+2)(x^2-\sqrt{3}x+2)=0\)
次に、解の公式を利用して\(x^2+\sqrt{3}x+2=0\)と\(x^2-\sqrt{3}x+2=0\)を計算しましょう。そうすると、以下が答えであるとわかります。
\(x=\displaystyle\frac{-\sqrt{3}±\sqrt{5}i}{2}\)
\(x=\displaystyle\frac{\sqrt{3}±\sqrt{5}i}{2}\)
こうして、4つの答えを得ることができました。
次数を下げ、計算を簡単にする
なお高次方程式の計算では、次数が大きいケースがあります。その場合、次数を下げることで計算を簡単にすることを考えましょう。
例題として、以下の問題を解くことで計算方法を学びましょう。
- \(f(x)=x^{2000}\)とします。\(x^2+x+1=0\)の解の一つがωのとき、\(f(ω)\)の値を一次式で記しましょう。
\(x^2+x+1=0\)の解の一つがωであるため、\(ω^2+ω+1=0\)です。そのため、以下の2つの式を作ることができます。
- \(ω^2+ω=-1\)
- \(ω^2=-ω-1\)
それでは、\(ω^3\)を計算してみましょう。以下のようになります。
\(ω^3\)
\(=ω·ω^2\)
\(=ω(-ω-1)\)
\(=-(ω^2+ω)\)
\(=1\)
こうして、\(ω^3=1\)であるとわかりました。そのため、以下のように計算できます。
\(f(ω)=ω^{2000}\)
\(f(ω)=ω^{3×666}·ω^2\)
\(f(ω)=1^{666}·(-ω-1)\)
\(f(ω)=-ω-1\)
こうして、\(f(ω)=-ω-1\)とわかりました。
二重解をもつ三次方程式の条件
次に、三次方程式が二重解をもつ条件を学びましょう。高次方程式では、二重解(または三重解)をもつことがあります。
例えば三次方程式の解が\(a\)と\(b\)の場合、以下の三次方程式は二重解をもちます。
- \(f(x)=(x-a)^2(x-b)\)
- \(f(x)=(x-a)(x-b)^2\)
なお、\(f(x)=(x-a)^3\)で表すことのできる三次方程式は三重解をもちます。こうした性質を利用して問題を解きましょう。以下の問題の答えは何でしょうか。
- \(f(x)=2x^3+ax^2+bx+3\)について、\(a\)と\(b\)は実数です。\(x=-1\)で重解となるとき、\(a\)、\(b\)、および\(x=-1\)以外の答えを求めましょう。
\(x=-1\)以外の答えを\(p\)とすると、以下の式を作ることができます。
- \(f(x)=2(x+1)^2(x-p)\)
そこで、先ほどの式を展開しましょう。
\(f(x)=2(x+1)^2(x-p)\)
\(f(x)=2(x^2+2x+1)(x-p)\)
\(f(x)=2(x^3-px^2+2x^2-2px+x-p)\)
\(f(x)=2x^3+(4-2p)x^2+(2-4p)x\)\(-2p\)
係数は一致する必要があるため、\(f(x)=2x^3+ax^2+bx+3\)と比較すると、以下の関係になるとわかります。
- \(4-2p=a\)
- \(2-4p=b\)
- \(-2p=3\)
\(-2p=3\)より、\(p=-\displaystyle\frac{3}{2}\)です。つまり、\(x=-1\)以外の答えは\(x=-\displaystyle\frac{3}{2}\)です。また\(p=-\displaystyle\frac{3}{2}\)であるため、\(a=7\)、\(b=8\)です。こうして、答えを得ることができました。
三次方程式の解と係数の関係
高次方程式の中でも、三次方程式では解と係数の関係を学びます。二次方程式で重要な解と係数の関係ですが、三次方程式にも解と係数の関係があるのです。なお三次方程式の解と係数の関係を学べば、四次方程式の解と係数の関係を理解することもできます。
以下の三次方程式があるとします。
- \(ax^3+bx^2+cx+d=0\)
この三次方程式の解を\(α\)、\(β\)、\(γ\)とすると、解と係数の関係は以下のようになります。
- \(α+β+γ=-\displaystyle\frac{b}{a}\)
- \(αβ+βγ+γα=\displaystyle\frac{c}{a}\)
- \(αβγ=-\displaystyle\frac{d}{a}\)
証明方法は簡単であり、因数定理を利用します。解が\(α\)、\(β\)、\(γ\)であるなら、三次方程式を以下のように因数分解できます。
\(ax^3+bx^2+cx+d\)
\(=a(x-α)(x-β)(x-γ)\)
そこで、この式を展開しましょう。
\(a(x-α)(x-β)(x-γ)\)
\(=a(x^2-(α+β)x+αβ)(x-γ)\)
\(=a(x^3-(α+β+γ)x^2\)\(+(αβ+βγ+γα)x\)\(-αβγ)\)
こうして係数を比較すると、先ほどの解と係数の関係を得ることができます。また三次方程式の解と係数の関係を忘れたとしても、因数定理による証明方法を知っていれば、公式を作ることができます。
参考までに、四次方程式でも同じように因数定理を利用することで解と係数の関係を得ることができます。四次方程式\(ax^4+bx^3+cx^2+dx+e=0\)の解を\(α\)、\(β\)、\(γ\)、\(δ\)とすると、解と係数の関係は以下のようになります。
- \(α+β+γ+δ=-\displaystyle\frac{b}{a}\)
- \(αβ+βγ+γδ+δα+αγ+βγ\)\(=\displaystyle\frac{c}{a}\)
- \(αβγ+βγδ+γδα+δαβ=-\displaystyle\frac{d}{a}\)
- \(αβγδ=\displaystyle\frac{e}{a}\)
因数定理を利用すれば、この関係を導き出すことができます。
解と係数の関係を利用して対称式の答えを得る
解と係数の関係を利用すれば、数学の問題を解けるケースは多いです。対称式に関する問題を解くとき、解と係数の関係がひんぱんに利用されます。
例えば\(3x^3-6x^2-9x+1=0\)の式について、解を\(α\)、\(β\)、\(γ\)とすると、\(α^2+β^2+γ^2\)の値はどうなるでしょうか。解と係数の関係より、以下のようになります。
- \(α+β+γ=2\)
- \(αβ+βγ+γα=-3\)
- \(αβγ=-\displaystyle\frac{1}{3}\)
また、\(α^2+β^2+γ^2\)を変形すると以下のようになります。
\(α^2+β^2+γ^2\)
\(=(α+β+γ)^2-2(αβ+βγ+γα)\)
\(=2^2-2×-3\)
\(=10\)
こうして、答えは10とわかりました。なお対称式に限らず、解と係数の関係を利用できる場面は多いです。
高次方程式が関わる問題を解く
二次方程式よりも計算が複雑になりやすい問題が高次方程式です。そこで、三次方程式や四次方程式の解き方を学びましょう。
高次方程式を解くためには、公式や置き換え、因数定理を利用します。場合によっては公式や因数定理を利用できないことがあるものの、因数分解することによって答えを得ることができます。
なお高次方程式の計算では、次数を下げたり、解と係数の関係を利用したりしましょう。これらの方法を利用しない場合、高次方程式の計算は複雑です。そこで計算を簡単にするための方法を学びましょう。
高次方程式の計算には解き方があります。三次方程式や四次方程式に関わる練習問題を解き、答えを得られるようになりましょう。






