関数を学ぶとき、最大値や最小値がどこになるのか理解する必要があります。ただ二次関数の場合、最大値と最小値の値が何になるのか理解しにくいです。
二次関数の問題では、\(x\)の範囲によって最大値や最小値が変わります。また二次関数の軸が移動するケースもあります。\(x\)の範囲が動く問題を解かなければいけないこともあります。二次関数では問題を解くときに場合分けする必要があり、最大値と最小値の値が複雑になりやすいのです。
二次関数で最大値と最小値の問題を解く場合、4パターンに分けることができます。そこで、それぞれの問題についてどのように解けばいいのか理解しましょう。
数字だけをみても二次関数の問題を解くことはできません。グラフを描くことによって、二次関数の最大値と最小値がわかります。そこで、二次関数の最大値と最小値の求め方を解説していきます。
もくじ
グラフの形と頂点によって最大値と最小値が異なる
まず、最も簡単な例から確認していきましょう。二次関数で\(x\)に範囲がない場合の最大値と最小値を考えてみましょう。このとき重要なのは\(a\)の値がプラスなのか、マイナスなのかを区別することです。
以下が二次関数の式です。
- \(y=ax^2+bx+c\)
\(a\)の値がプラスの場合、下に凸のグラフになります。下に凸のグラフでは、必ず頂点が最小値になります。一方で\(a\)の値がマイナスの場合、上に凸のグラフになります。上に凸のグラフでは、必ず頂点が最大値になります。
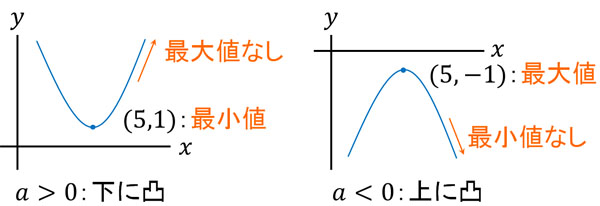
つまり頂点がわかれば、最大値(または最小値)がわかります。
なお\(x\)に範囲がない場合、下に凸(\(a>0\))のグラフでは最大値がありません。\(x\)の値は無限に増えることが可能であり、\(y\)の値も無限に大きくなるからです。同じように考えると、上に凸(\(a<0\))のグラフでは最小値がありません。\(x\)の値が無限に増えると、\(y\)の値は無限に小さくなるからです。
平方完成によって頂点を調べる
前述のとおり、頂点の場所を調べることによって最大値(または最小値)を出すことができます。そこで、平方完成をすることで頂点の場所を調べましょう。
また二次関数の最大値または最小値を出すとき、グラフを描けることが重要です。グラフを描くことができない場合、二次関数の最大値または最小値を求めるのは難しいです。グラフを描くことによって、最大値や最小値の座標が視覚的にわかるようになります。
二次関数のグラフを描く手順は以下のとおりです。
- \(a\)の値がプラスなのか、マイナスなのか確認する
- 平方完成を行い、頂点の場所を調べる
- \(y\)軸との交点と頂点を滑らかな曲線で結ぶ
例えば、以下の二次関数の最大値と最小値は何でしょうか。
- \(y=2x^2-8x+11\)
まずは平方完成をしてみましょう。以下のようになります。
\(y=2x^2-8x+11\)
\(y=2(x^2-4x)+11\)
\(y=2(\color{red}{x^2-4x+4}-4)+11\)
\(y=2(x^2-4x+4)+3\)
\(y=2(x-2)^2+3\)
このように平方完成することによって、頂点は\((2,3)\)であるとわかります。また\(a>0\)なので下に凸のグラフです。また\(x=0\)を代入すると、\(y\)軸との交点は11になります。そこで、以下のように頂点で\(y\)軸との交点を結びましょう。

こうして最小値\((2,3)\)、最大値なしであるとわかります。
二次関数の最大値・最小値を求める問題は4パターン
なお、二次関数の問題で最大値と最小値を求める場合、4パターンに分けることができます。そこで、すべてのパターンで問題を解けるようにしましょう。以下の4パターンです。
- \(x\)の範囲がない場合の最大値と最小値
- \(x\)の範囲がある場合の最大値と最小値
- 軸が動く場合の最大値と最小値
- \(x\)の範囲が動く場合の最大値と最小値
範囲がない場合の最大値と最小値については先ほど説明しました。そこで、ほかの3パターンについて確認していきます。ただ、その前に\(x\)の範囲や軸の位置によって、どのように最大値と最小値が変化するのか理解しなければいけません。
最大値と最小値の変化を学べば、すべてのパターンで二次関数の最大値と最小値の問題を解けるようになります。以下のとき、最大値と最小値の場所が変わります(下に凸である\(a>0\)のグラフで説明しています)。

\(x\)の範囲や軸の位置によって、最大値と最小値が変化することがわかります。これが、二次関数のグラフを描ける必要がある理由になります。グラフを描かないと、最大値と最小値を見つけるのが難しいのです。
それでは、最大値と最小値の変化をより詳しく確認していきましょう。
・最大値の変化
\(x\)の値が変化することによって、最大値はどのように変わるのでしょうか。図にすると、以下のようになります。
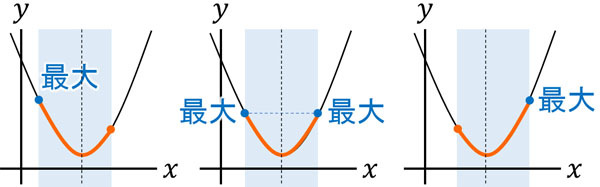
このように、3パターンに分けることができます。最大値がどこで変わるのか確認すると、「\(x\)の範囲の中点」が頂点の\(x\)座標と重なるとき、最大値が変化します。つまり最大値では、二次関数の頂点に対して、\(x\)の範囲の中点がどこにあるのかを確認すればいいとわかります。
・最小値の変化
一方で最小値はどのように変化するのでしょうか。\(x\)の範囲によって、以下のように最小値が変わります。

二次関数の最小値では、\(x\)の範囲が頂点を含んでいるかどうかを確認しましょう。\(x\)の範囲が頂点を含んでいる場合、頂点が最小値です。一方で\(x\)の範囲が頂点を含んでいない場合、\(x\)の範囲の右端または左端が最小値です。
ここまでの内容を理解すれば、二次関数の最大値と最小値を見つけやすくなります。
範囲がある場合の最大値と最小値
それでは、\(x\)の範囲がある場合の最大値と最小値について確認していきましょう。例えば、以下の二次関数があるとします。
- \(y=(x-2)^2+2\)
\(x\)の範囲が\(0≦x≦a\)の場合、最大値と最小値はどのように変化するでしょうか。先に述べた通り、最大値と最小値は以下のときに変わります。
- 最大値:\(x\)の範囲の中点が頂点の\(x\)座標と重なるとき
- 最小値:\(x\)の範囲が頂点を含むとき
そこで、グラフを描いて考えてみましょう。まず、最大値から確認していきます。
・最大値を求める
\(y=(x-2)^2+2\)の頂点は\((2,2)\)です。\(x\)の範囲の中点が頂点の\(x\)座標と重なるとき、最大値が二カ所になります。つまり\(a=4\)であり、\(x\)の範囲が\(0≦x≦4\)のとき、最大値が二カ所になります。\(0≦x≦4\)の中点は\(x=2\)であり、頂点の\(x\)軸と同じだからです。
つまり、\(a\)の値が4に比べて大きいのか、それとも小さいのかによって最大値が変化します。具体的には、以下の場合分けをしましょう。
- \(0<a<4\)
- \(a=4\)
- \(4<a\)
図にすると以下のようになります。
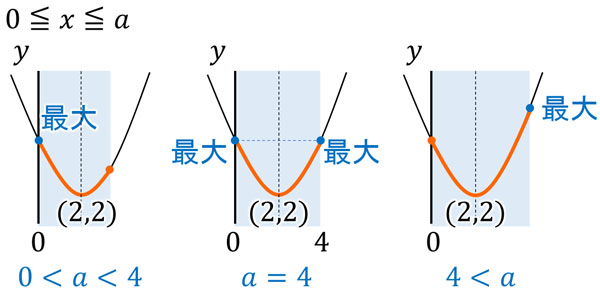
・\(0<a<4\)のとき
\(x=0\)のとき、最大値になります。\(y=(x-2)^2+2\)に\(x=0\)を代入すると、\(y=6\)です。そのため、最大値は6です。
・\(a=4\)のとき
\(x=0\)または\(x=4\)のとき、最大値になります。\(y=(x-2)^2+2\)に\(x=0\)または\(x=4\)を代入すると、\(y=6\)です。そのため、最大値は6です。
・\(4<a\)のとき
\(x=a\)のとき、最大値になります。\(y=(x-2)^2+2\)に\(x=a\)を代入すると、\(y=a^2-4a+6\)です。そのため、最大値は\(a^2-4a+6\)です。
これらをまとめると、\(0<a≦4\)のとき最大値は6となり、\(4<a\)のとき最大値は\(a^2-4a+6\)となります。
・最小値を求める
次に最小値を求めましょう。\(x\)の範囲が頂点を含むかどうかによって最小値が変化します。頂点の座標は\((2,2)\)です。そのため、\(a\)が2よりも大きいのか小さいのかによって最小値が変化します。具体的には、以下の場合分けをしましょう。
- \(0<a<2\)
- \(2≦a\)
\(0≦x≦a\)であるため、左端は固定されています。そのため\(2≦a\)の場合、必ず頂点を含むようになります。図にすると以下のようになります。

・\(0<a<2\)のとき
\(x=a\)のとき、最小値になります。\(y=(x-2)^2+2\)に\(x=a\)を代入すると、\(y=a^2-4a+6\)です。そのため、最小値は\(a^2-4a+6\)です。
・\(2≦a\)のとき
\(x=2\)のとき、最小値になります。頂点は\((2,2)\)なので、最小値は2です。
二次関数のグラフを描くことによって、最大値と最小値がわかるようになります。そのため、問題を解くときは必ずグラフを描くようにしましょう。
軸が動く場合の二次関数での最大値と最小値
次に、軸が動く場合の二次関数を考えます。例えば以下の二次関数では、\(a\)の値が変化することによって軸が動きます。
- \(y=(x-a)^2+2\)
この関数の頂点は\((a,2)\)です。\(a\)の値が変化すると頂点が動きます。頂点が動くというのは、軸が動くことを意味しています。そこで\(0≦x≦4\)のとき、二次関数の最大値と最小値を求めましょう。
・最大値を求める
二次関数の最大値を求めるとき、必ず図を描きましょう。また\(x\)の範囲の中点と軸(頂点)が同じ値のとき、最大値が変化します。\(0≦x≦4\)であるため、\(x\)の範囲の中点は2です。また頂点は\((a,2)\)なので、\(a=2\)のときに最大値が変化します。
図にすると以下のようになります。
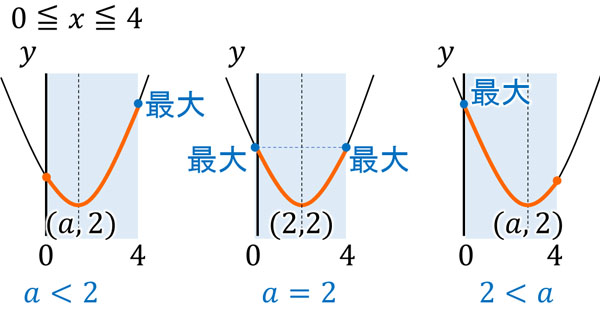
軸が動くというのは、二次関数のグラフが右(または左)に平行移動することを意味します。また図を描くと、どこが最大値なのかわかりやすくなります。\(a=2\)のときに最大値が変わるため、以下のように場合分けをしましょう。
・\(a<2\)のとき
\(x=4\)のとき、最大値になります。\(y=(x-a)^2+2\)に\(x=4\)を代入すると、\(y=a^2-8x+18\)です。そのため、最大値は\(a^2-8x+18\)です。
・\(a=2\)のとき
\(x=0\)または\(x=4\)のとき、最大値になります。\(y=(x-a)^2+2\)に\(x=0,a=2\)または\(x=4,a=2\)を代入すると、\(y=6\)です。そのため、最大値は6です。
・\(2<a\)のとき
\(x=0\)のとき、最大値になります。\(y=(x-a)^2+2\)に\(x=0\)を代入すると、\(y=a^2+2\)です。そのため、最大値は\(a^2+2\)です。
・最小値を求める
一方、最小値は\(x\)の範囲が頂点を含むかどうかで変化します。\(0≦x≦4\)なので、\(a\)の値(軸)が\(0≦x≦4\)にあるかどうかで場合分けをしましょう。図にすると以下のようになります。
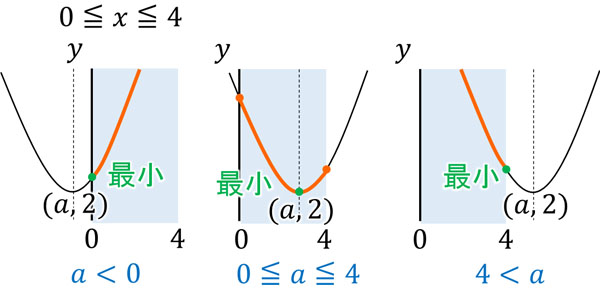
・\(a<0\)のとき
\(x=0\)のとき、最小値になります。\(y=(x-a)^2+2\)に\(x=0\)を代入すると、\(y=a^2+2\)です。そのため、最小値は\(a^2+2\)です。
・\(0≦a≦4\)のとき
\(x=a\)のとき、最小値になります。\(y=(x-a)^2+2\)に\(x=a\)を代入すると、\(y=2\)です。そのため、最小値は2です。または頂点が\((a,2)\)のため、計算しなくても最小値は2であるとわかります。
・\(4<a\)のとき
\(x=4\)のとき、最小値になります。\(y=(x-a)^2+2\)に\(x=4\)を代入すると、\(y=a^2-8x+18\)です。そのため、最小値は\(a^2-8x+18\)です。
範囲が動く場合の二次関数での最小値と最大値
次は\(x\)の範囲が動く場合の二次関数を理解しましょう。例えば\(a≦x≦a+4\)であれば、\(a\)の値が変化することによって\(x\)の範囲が動きます。例として\(x\)の範囲が\(a≦x≦a+4\)のとき、以下の二次関数の最大値と最小値を求めましょう。
- \(y=(x-2)^2+2\)
問題の解き方はこれまで説明した方法と同じです。\(a\)の値によって場合分けをしましょう。
・最大値を求める
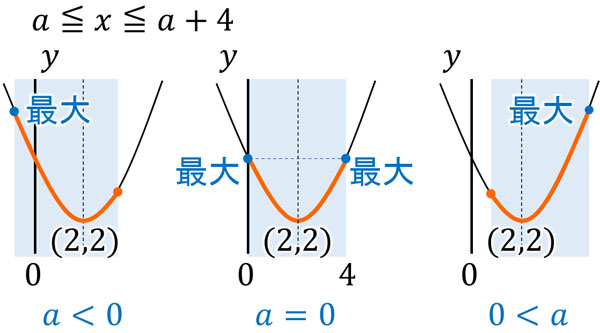
\(a≦x≦a+4\)の場合、\(x\)の範囲の中点は\(a+2\)です。また、\(y=(x-2)^2+2\)の頂点は\((2,2)\)です。そのため\(a+2=2\)のとき、最大値が変化します。つまり\(a=0\)を境にして最大値が変わります。図にすると以下のようになります。
そこで、場合分けすることによって最大値を求めましょう。
・\(a<0\)のとき
\(x=a\)のとき、最大値になります。\(y=(x-2)^2+2\)に\(x=a\)を代入すると、\(y=a^2-4a+6\)です。そのため、最大値は\(a^2-4a+6\)です。
・\(a=0\)のとき
\(x=0\)または\(x=4\)のとき、最大値になります。\(y=(x-2)^2+2\)に\(x=0\)または\(x=4\)を代入すると、\(y=6\)です。そのため、最大値は6です。
・\(0<a\)のとき
\(x=a+4\)のとき、最大値になります。\(y=(x-2)^2+2\)に\(x=a+4\)を代入すると、\(y=a^2+4a+6\)です。そのため、最大値は\(a^2+4a+6\)です。
・最小値を求める
\(x\)の範囲が頂点を含むかどうかによって最小値が変わります。頂点は\((2,2)\)です。そのため、\(a≦x≦a+4\)が2(頂点の\(x\)座標)を含むかどうかによって場合分けをしましょう。以下のようになります。
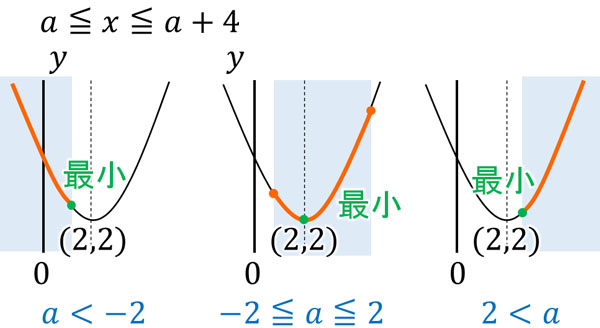
・\(a+4<2\)、つまり\(a<-2\)のとき
\(x=a+4\)のとき、最小値になります。\(y=(x-2)^2+2\)に\(x=a+4\)を代入すると、\(y=a^2+4a+6\)です。そのため、最小値は\(a^2+4a+6\)です。
・\(a≦2≦a+4\)、つまり\(-2≦a≦2\)のとき
\(x=2\)のとき、最小値になります。\(y=(x-2)^2+2\)に\(x=2\)を代入すると、\(y=2\)です。そのため、最小値は2です。また頂点は\((2,2)\)であるため、計算をしなくても最小値は2であるとわかります。
・\(2<a\)のとき
\(x=a\)のとき、最小値になります。\(y=(x-2)^2+2\)に\(x=a\)を代入すると、\(y=a^2-4a+6\)です。そのため、最小値は\(a^2-4a+6\)です。
場合分けを利用し、二次関数の最大値と最小値を見つける
二次関数で最大値と最小値を見つけるとき、必ずグラフを描くようにしましょう。そうしなければ、どこが最大値または最小値になるのか理解しにくいです。
なお二次関数で最大値と最小値を求めるとき、4つのパターンがあります。ただ、解き方は似ています。最大値を出すとき、\(x\)の範囲の中点で最大値が変わります。また最小値を出すとき、\(x\)の範囲が頂点を含むかどうかによって最小値が変わります。
この性質を利用すれば、すべてのパターンで二次関数の最大値と最小値を求めることができます。
問題を解くためにグラフを描く必要はあるものの、解き方を理解すれば二次関数の最大値と最小値がわかります。そこで、どのように考えて最大値と最小値を出せばいいのか理解しましょう。






