特殊な漸化式は多く、その中に和\(S_n\)を含む漸化式があります。数列での和の性質を利用することにより、和を含む漸化式を解くことになります。
漸化式は解き方が決まっているため、解き方を覚えていなければ答えを得るのは難しいです。ヒントなしに漸化式の答えを得るのは難易度が高いです。そこで和を含む漸化式について、どのように計算すればいいのか覚えましょう。
それでは、和を含む漸化式に関する問題では具体的にどのように一般項を計算すればいいのでしょうか。和を含む漸化式の計算方法を解説していきます。
もくじ
和\(S_n\)と一般項\(a_n\)の関係と公式
和を含む漸化式を理解するため、和\(S_n\)と一般項\(a_n\)の関係を復習しましょう。数列の和\(S_n\)がわかっている場合、一般項\(a_n\)を計算できます。以下のように、\(S_n\)と\(S_{n-1}\)を利用すればいいです。
- \(S_n-S_{n-1}=a_n\)
- \(n≧2\)
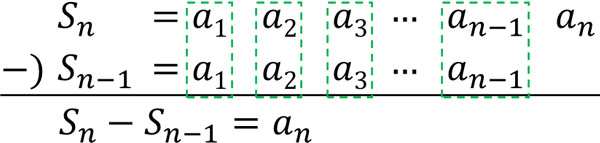
ただ漸化式では、\(n\)を\(n+1\)に変えるときの式がひんぱんに利用されます。そこで\(S_n\)と\(S_{n-1}\)ではなく、\(S_n\)と\(S_{n+1}\)を利用しましょう。この場合、\(a_{n+1}\)を得ることができます。
- \(S_{n+1}-S_n=a_{n+1}\)
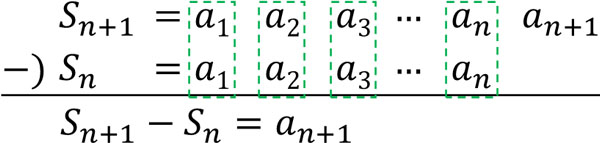
公式として覚えなくても、容易に理解できると思います。ここまでの内容を理解して、和を含む漸化式の問題を解けるようになりましょう。
和\(S_n\)を含む漸化式で初項を計算する
それでは、例題を用いて和\(S_n\)を含む漸化式の一般項\(a_n\)を求めましょう。以下の問題の答えは何でしょうか。
- 数列\(\{a_n\}\)について、初項から第\(n\)項までの和が\(S_n=7a_n-3-3n\)のとき、一般項\(a_n\)を求めましょう。
和\(S_n\)を含む漸化式では、\(a_n\)のみを含む式に変える必要があります。そこで、まずは初項\(a_1\)を計算しましょう。\(S_1=a_1\)であるため、以下の式を作れます。
\(S_1=7a_1-3-3×1\)
\(a_1=7a_1-6\)
\(-6a_1=-6\)
\(a_1=1\)
こうして、初項は\(a_1=1\)とわかりました。
項数をずらし、漸化式を変形する
次に、\(S_n\)と\(S_{n+1}\)を利用して式を作ります。問題文より、\(S_{n+1}\)は以下のように表すことができます。
\(S_{n+1}=7a_{n+1}-3-3(n+1)\)
\(S_{n+1}=7a_{n+1}-6-3n\)
そこで、以下のように計算しましょう。
\(S_{n+1}-S_n=a_{n+1}\)
\(7a_{n+1}-6-3n\)\(-(7a_n-3-3n)\)\(=a_{n+1}\)
\(6a_{n+1}=7a_n+3\)
\(a_{n+1}=\displaystyle\frac{7}{6}a_n+\displaystyle\frac{1}{2}\)
こうして和\(S_n\)を含む漸化式について、\(S_n\)を含まない漸化式へ変形することができました。
特性方程式を利用し、一般項を得る
\(a_n\)を含む漸化式を作れば、漸化式を利用することで一般項を計算すればいいです。先ほどの式について、特性方程式を利用しましょう。
\(α=\displaystyle\frac{7}{6}α+\displaystyle\frac{1}{2}\)
\(-\displaystyle\frac{1}{6}α=\displaystyle\frac{1}{2}\)
\(α=-3\)
特性方程式を解くと\(α=-3\)になるため、先ほどの漸化式を以下のように変形できます。
- \(a_{n+1}+3=\displaystyle\frac{7}{6}(a_n+3)\)
数列\(\{a_n+3\}\)は初項\(a_1+3=4\)、公比\(\displaystyle\frac{7}{6}\)の等比数列です。そのため、以下のように一般項\(a_n\)を計算しましょう。
\(a_n+3=4·\left(\displaystyle\frac{7}{6}\right)^{n-1}\)
\(a_n=4·\left(\displaystyle\frac{7}{6}\right)^{n-1}-3\)
こうして、一般項を得ることができました。和を含む漸化式では、\(S_n\)を消去することを考えましょう。そうすれば、一般項を得られます。
和を含む漸化式の計算方法を学ぶ
数列の和を利用することにより、一般項\(a_n\)を計算できます。また漸化式では、\(S_n\)と\(S_{n+1}\)を利用することで\(a_{n+1}\)を作れます。この性質を利用することにより、漸化式の計算が可能です。
\(S_{n+1}-S_n=a_{n+1}\)であり、\(S_1=a_1\)です。この性質を利用することにより、漸化式を変形しましょう。
漸化式で\(S_n\)を消去できれば、あとは漸化式の計算をするだけです。特性方程式を利用することによって一般項を計算しましょう。






