特定の図形を表すとき、方程式を作れるようになる必要があります。直線の方程式であれば、\(y=ax+b\)を利用します。それでは、円の方程式はどのように表せばいいのでしょうか。
円の方程式は\((x-a)^2+(y-b)^2=r^2\)によって表すことができます。この公式を利用することにより、円の半径と座標がわかります。また、一般形\(\)を利用することによっても円の方程式を得ることができます。
そこで条件が与えられたとき、どのような円を表しているのか計算できるようになりましょう。円の一般形を基本形へ変形することにより、円の半径と座標を得ることも重要です。
それでは、どのように円の方程式を利用して計算すればいいのでしょうか。公式の利用法や証明、練習問題を含めて解説していきます。
もくじ
円の方程式の公式:基本形の公式と証明
まず、円の方程式を覚えましょう。点\((a,b)\)を中心とする、半径\(r\)の円の方程式は以下のようになります。
- \((x-a)^2+(y-b)^2=r^2\)
例えば円の中心が\((3,-2)\)であり、半径4の円は以下のように表すことができます。
- \((x-3)^2+(y+2)^2=16\)
それでは、なぜこの公式を利用することで円を表すことができるのでしょうか。証明方法は簡単であり、円の半径\(r\)を計算するとき、以下の式を作ることができます。
- \(\sqrt{(x-a)^2+(y-b)^2}=r\)
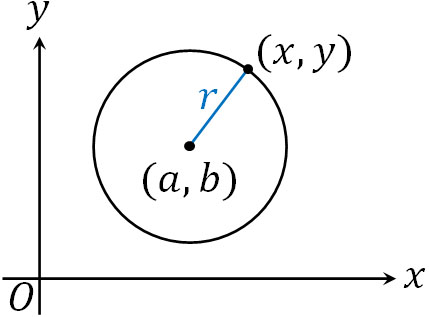
そこで、両辺を二乗しましょう。そうすると、先ほど記した公式を得ることができます。
円の方程式の計算方法:中心と円上の点がわかっている
それでは、円の方程式を計算してみましょう。以下の問題の答えは何でしょうか。
- 中心が\((1,2)\)であり、点\((5,5)\)を通る円の方程式を求めましょう。
中心は\((1,2)\)であるため、以下の式を作ることができます。
- \((x-1)^2+(y-2)^2=r^2\)
また点\((5,5)\)を通るため、この式に代入しましょう。
\((5-1)^2+(5-2)^2=r^2\)
\(16+9=r^2\)
\(r^2=25\)
こうして、円の方程式は\((x-1)^2+(y-2)^2=25\)とわかりました。
一般形の円の方程式
ここまで、円の方程式の基本形を解説してきました。次に、円の方程式の一般形を学びましょう。直線の方程式であれば、\(y=ax+b\)が基本形であり、\(ax+by+c=0\)が一般形です。円の方程式についても、同じように一般形が存在します。
円の方程式の一般形は以下になります。
- \(x^2+y^2+ax+by+c=0\)
円の方程式で一般形は特殊であり、一般形を確認しても円の半径と中心座標はわかりません。ただ円を表す方程式であるため、この式で記しても正解です。
それでは、どのようなときに円の一般形を利用するのでしょうか。3つの点が与えられており、3点を通る円の方程式を得たい場合は一般形を用いましょう。以下の問題の答えは何でしょうか。
- 3点A\((2,3)\)、B\((2,1)\)、C\((4,1)\)を頂点とする△ABCの外接円の方程式を計算しましょう。
△ABCの外接円の方程式とは、要は3点を通る円の方程式を計算すればいいです。円の中心と半径はわかっていないため、一般形の式に代入した後、連立方程式を解くことで答えを得ましょう。以下のようになります。
- A\((2,3)\)より:\(2a+3b+13+c=0\) – ①
- B\((2,1)\)より:\(2a+b+5+c=0\) – ②
- C\((4,1)\)より:\(4a+b+17+c=0\) – ③
・①と②より
\(2b+8=0\)
\(b=-4\)
・②と③より
\(2a+12=0\)
\(a=-6\)
\(a=-6\)と\(b=-4\)より、\(c=11\)です。こうして、円の方程式は\(x^2+y^2-6x-4y+11=0\)とわかりました。
方程式の表す図形:中心と半径を得る
なお円の方程式について、一般形の式を見ても円の中心や半径はわかりません。そこで一般形を基本形へ変形する方法を学びましょう。二乗を作ることにより、基本形の式を作ることができます。
それでは、先ほど計算した一般形の式\(x^2+y^2-6x-4y+11=0\)を基本形の式へ変形してみましょう。
\(x^2+y^2-6x-4y+11=0\)
\(x^2-6x+y^2-4y+11=0\)
\((x^2-6x+9-9)\)\(+(y^2-4y+4-4)\)\(+11=0\)
\((x-3)^2+(y-2)^2=2\)
こうして中心が\((3,2)\)、半径が\(\sqrt{2}\)の円であるとわかりました。
座標軸に接する円
それでは、ここまでの知識を利用して応用問題を解いてみましょう。座標軸に接する円について、以下の問題の答えは何でしょうか。
- 点\((2,1)\)を通り、\(x\)軸と\(y\)軸に接する円の方程式を求めましょう。
\(x\)軸と\(y\)軸に接する円では、以下のように\(x\)座標と\(y\)座標の絶対値が必ず同じ値になります。

問題文より、円は点\((2,1)\)を通るため、円の中心を\((a,a)\)と表すことができます。また、円の半径は\(a\)です。そのため、円の方程式は以下のようになります。
- \((x-a)^2+(y-a)^2=a^2\)
円は点\((2,1)\)を通るため、値を代入しましょう。
\((2-a)^2+(1-a)^2=a^2\)
\(a^2-4a+4\)\(+a^2-2a+1\)\(=a^2\)
\(a^2-6a+5=0\)
\((a-1)(a-5)=0\)
こうして、\(a=1\)と\(a=5\)であればいいとわかります。つまり、以下の2つが答えです。
- \((x-1)^2+(y-1)^2=1\)
- \((x-5)^2+(y-5)^2=25\)
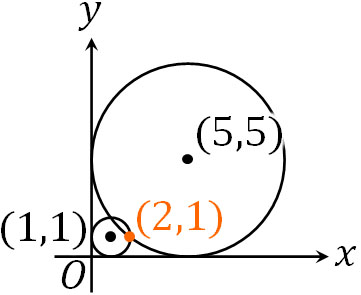
問題文を確認し、どのような図形を描くことができるのかを理解すれば、これまで学んだ知識を利用することで答えを得ることができます。
円の方程式を利用し、円を表現する
直線の方程式と同様に円の方程式は重要です。公式を利用することにより、数式によって円を表現できるようになりましょう。
基本形の式は円の方程式で最も利用され、式を確認することで円の中心と半径がわかります。ただ場合によっては、一般形の式を利用して円を表現することもあります。そこで、基本形と一般形の両方を利用できるようになりましょう。
なお、円の一般形の式では中心と半径がわかりません。そこで、一般形を基本形へ変形できるようになる必要があります。
円に関する図形の問題を解く場合、円の方程式を利用できる必要があります。そこで公式を利用して、円を表現できるようになりましょう。






