二次方程式では、実数解の個数を計算する方法として判別式(\(D\))を利用します。判別式の値がプラスまたは0の場合、実数解をもちます。
一方で三次方程式ではどのように実数解の個数を計算すればいいのでしょうか。三次方程式の場合、実数解を数えるときに複数の方法があります。式によって計算方法が異なり、主に3つの方法に分けることができます。
また三次関数の計算をするとき、微分を利用することが頻繁にあります。三次方程式についても、実数解の個数を計算するとき、微分を用いて答えを見つけましょう。
そこでどのようにして、三次方程式の実数解の個数を見つければいいのかに解説していきます。
もくじ
三次方程式の実数解の個数を数える
実数解があるとは、どういう意味なのでしょか。三次方程式の実数解の個数を理解するため、まず二次方程式について実数解の個数の数え方を復習しましょう。二次方程式の場合、以下のような式になります。
- \(ax^2+bx+c=0\)
この方程式では、\(x\)に何かの値を代入することによって、答えが0になるときに「実数解をもつ」となります。\(y=ax^2+bx+c\)の式において、\(y=0\)となる\(x\)の値というのは、要は「\(x\)軸との交点があるかどうか」を考えればいいです。
そのため、二次方程式で実数解をもつかどうかについては以下のグラフによって判断できます。
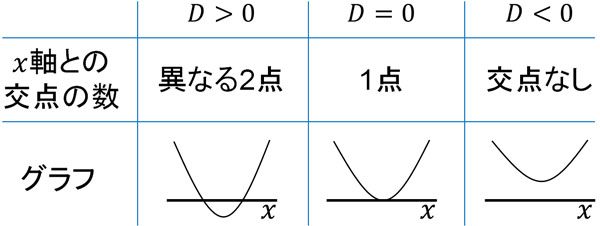
グラフの状態を判断するため、私たちは判別式(\(D\))を利用します。判別式によって、二次方程式が\(x\)軸と交点をもつかどうかがわかるのです。
極値を利用し、三次方程式の実数解の個数を数える
一方で三次関数の場合、二次関数とはグラフの形が異なります。そのため三次関数では、二次関数とは異なる方法によって計算しなければいけません。
三次関数の場合、極大値と極小値があります。そこで極値を利用して、実数解の個数を数えましょう。三次方程式では、以下のように実数解の個数を考えます。
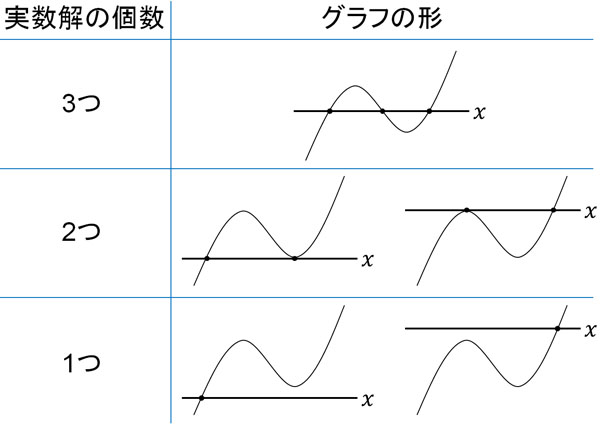
このように、三次方程式では実数解が1つ、2つ、3つのどれかになります。
また三次方程式で重要になるのが極値です。極大値と極小値について、\(y\)の値がプラスなのかマイナスなのかを確認するのです。これによって、実数解の個数がいくつあるのか数えることができます。
三次関数での極値の位置を調べるとき、私たちは微分をします。そのため、三次方程式での実数解の個数を調べるとき、微分をしなければいけないと理解しましょう。
実数解の個数を数える方法は3つある
それでは、具体的にどのようにして三次方程式の実数解の個数を調べればいいのでしょうか。これには、主に以下の方法があります。
- \(x\)軸との共有点を確認し、実数解を数える
- 方程式と定数\(a\)を分け、共有点の数を数える
- 定数\(a\)を分けられない場合、極大値と極小値のかけ算をする
三次方程式が定数\(a\)を含んでいるのかどうかによって計算方法が変わります。すべての方法について、計算できるようにしましょう。
\(x\)軸との共有点を確認し、実数解を数える
三次方程式の実数解の個数を数えるとき、最も計算しやすいのが「式の中に定数\(a\)が存在しないパターン」です。この場合、極値の符号を確認することによって実数解の答えを得ることができます。
極大値と極小値について、\(y\)の値を計算するとき、符号に着目しましょう。以下のように、極値の\(y\)座標がプラスなのかマイナスなのか、または0なのかによって実数解の答えが変わります。
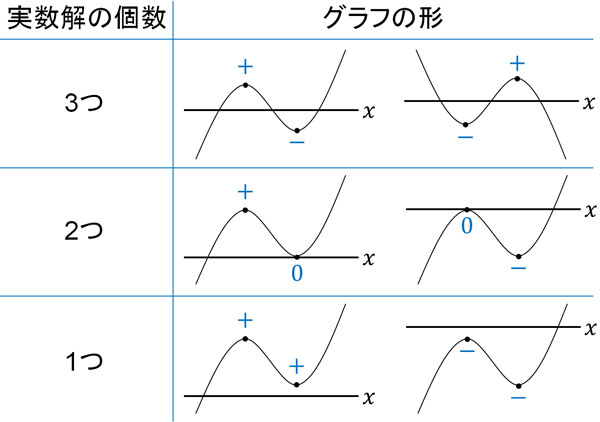
そこで、実際にグラフを描いてみましょう。例えば、以下の答えは何でしょうか。
- \(x^3-6x^2+9x+2=0\)の三次方程式について、実数解の個数はいくらでしょうか。
極値を調べるため、まずは微分しましょう。\(f(x)=x^3-6x^2+9x+2\)とすると、以下のようになります。
- \(f'(x)=3x^2-12x+9\)
また、因数分解すると以下のようになります。
\(f'(x)=3x^2-12x+9\)
\(f'(x)=3(x^2-4x+3)\)
\(f'(x)=3(x-1)(x-3)\)
こうして\(x=1,3\)のとき、この三次関数は極値をもつとわかります。また\(x=1\)と\(x=3\)を代入するとき、\(y\)の値は以下のようになります。
\(f(1)=1-6+9+2=6\)
\(f(3)=27-54+27+2=2\)
そのため、以下のグラフを描くことができます。
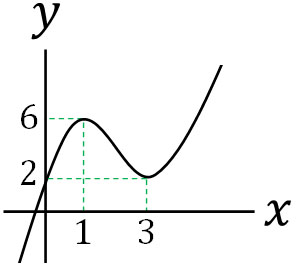
極値が両方ともプラスであるため、三次関数は\(x\)軸と1つの交点をもちます。つまり三次方程式の実数解の個数は1つです。
方程式と定数\(a\)を分け、共有点の数を数える
一方、式の中に定数\(a\)を含む場合はどのように計算すればいいのでしょうか。\(a\)の値によって実数解の個数が変わるため、場合分けをすることによって答えを出さなければいけません。
定数\(a\)を分けることができる場合、三次方程式と定数を分離しましょう。例えば、以下の答えは何でしょうか。
- \(x^3-6x^2+9x+2-a=0\)の三次方程式について、実数解の個数はいくらでしょうか。
先ほど三次方程式について、定数\(a\)を加えました。この場合について、実数解の答えを計算しましょう。そこで、以下のように定数\(a\)と三次方程式を分けます。
- \(x^3-6x^2+9x+2=a\)
この式は何を意味しているのでしょうか。\(x^3-6x^2+9x+2=0\)のように右辺が0の場合、\(y=0\)となる\(x\)の値を見つければいいため、\(x\)軸との交点を見つければよかったです。
一方、今回は右辺が\(y=a\)となっています。つまり、\(x^3-6x^2+9x+2\)と\(y=0\)(\(x\)軸)の交点を見つけるのではなく、\(x^3-6x^2+9x+2\)と\(y=a\)の交点を見つければいいと考えることができます。

\(y=x^3-6x^2+9x+2\)のグラフは形が決まっています。一方で定数\(a\)にはあらゆる数字を入れることができ、\(y=a\)のグラフは動くことができます。つまり\(a\)の値によって、交点の数が変わります。
そこでグラフより、以下のように場合分けをしましょう。
・\(a<2\),\(6<a\)のとき
実数解は1つ
・\(a=2\)または\(a=6\)のとき
実数解は2つ
・\(2<a<6\)のとき
実数解は3つ
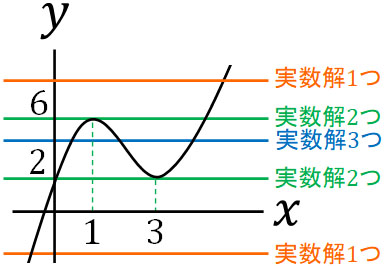
定数\(a\)の値が変わることによって、実数解の個数も変化します。そこで方程式の意味を理解し、実数解の答えを出すようにしましょう。
定数\(a\)を分けられない場合、極大値と極小値のかけ算をする
ただ三次方程式では、定数\(a\)を分けられないケースがあります。この場合、どのようにして実数解の個数を数えればいいのでしょうか。
例として、以下の問題を解いてみましょう。
- \(x^3-3ax+2=0\)の三次方程式について、実数解の個数が一つとなる\(a\)の範囲を求めましょう。
つまり、\(x\)軸と一点のみ交わる\(a\)の値を出せばいいとわかります。この式について、先ほどと同様に以下の式を作って計算することは可能です。
- \(\displaystyle\frac{x^3+2}{3x}=a\)
ただ\(f(x)=\displaystyle\frac{x^3+2}{3x}\)のグラフを描くのは大変です。そこで、ほかの方法によって計算しましょう。具体的には、\(f(x)=x^3-3ax+2\)の極大値と極小値を求めましょう。
先ほど極値の値によって三次方程式での実数解の個数が変わることを説明しました。再び図を掲載すると、以下のようになります。

言い換えると、極大値と極小値のかけ算をした後、符号がプラスなのかマイナスなのか、または0なのかによって実数解の答えが変化します。
- 極大値と極小値のかけ算で答えがマイナス:実数解は3つ
- 極大値と極小値のかけ算で答えが0:実数解は2つ
- 極大値と極小値のかけ算で答えがプラス:実数解は1つ
このように理解しましょう。極大値と極小値を計算し、かけ算をすることによって実数解の個数を確認できます。そこで\(f(x)=x^3-3ax+2\)として、以下のように微分しましょう。
- \(f'(x)=3x^2-3a\)
因数分解すると以下のようになります。
\(f'(x)=3x^2-3a\)
\(f'(x)=3(x^2-a)\)
\(f'(x)=3(x+\sqrt{a})(x-\sqrt{a})\)
こうして\(x=-\sqrt{a},\sqrt{a}\)のときに極値になることがわかります。また、\(x=-\sqrt{a},\sqrt{a}\)を代入して、極大値と極小値の\(y\)の値を計算しましょう。以下のようになります。
\(f(\sqrt{a})=a\sqrt{a}-3a\sqrt{a}+2\)\(=2-2a\sqrt{a}\)
\(f(-\sqrt{a})=-a\sqrt{a}+3a\sqrt{a}+2\)\(=2+2a\sqrt{a}\)
そこで、以下の計算をしましょう。
\(f(\sqrt{a})×f(-\sqrt{a})\)
\(=(2-2a\sqrt{a})(2+2a\sqrt{a})\)
\(=4-4a^3\)
極大値と極小値をかけて答えがプラスになる場合、三次方程式は1つの実数解をもちます。そのため以下のとき、実数解は一つになります。
\(4-4a^3>0\)
\(a^3-1<0\)
\((a-1)(a^2+a+1)<0\)
\(y=a^2+a+1\)とすると、この二次関数は\(x\)軸との交点がありません。判別式(\(D\))がマイナスになるからです。つまり、常に\(a^2+a+1>0\)となります。そのため、\((a-1)(a^2+a+1)<0\)になるためには、\((a-1)\)がマイナスになるかどうかを確認すればいいとわかります。
つまり以下のとき、\((a-1)(a^2+a+1)<0\)となります。
\(a-1<0\)
\(a<1\)
こうして\(a<1\)のとき、三次方程式は1つの実数解をもつようになります。
三次関数を微分し、極値を求めて実数解の個数を確認する
高校数学で微分を学ぶとき、三次方程式について実数解の個数を求める問題が出されます。問題を解くためには極値を利用しなければいけません。そこで、三次関数の微分をしましょう。
微分によって極大値と極小値がわかれば、三次関数のグラフを描くことができます。これによって、\(x\)軸との交点や\(y=a\)との交点を求めることができます。
また場合によっては、定数\(a\)を分けられないことがあります。この場合、極大値と極小値をかけましょう。かけ算の答えがプラスの場合、実数解は1つです。一方でかけ算の答えが0だと、実数解は2つです。かけ算の答えがマイナスの場合、実数解は3つです。
三次関数の微分をすれば、三次方程式の実数解の個数を数えられるようになります。極大値と極小値を利用して、実数解の個数がいくつあるのか確認しましょう。