順列（P）の公式と階乗の計算方法

確率を学ぶとき、高校数学では順列（Permutations）を習います。順列というのは、小学算数や中学数学では「並べかた」という名前で学びました。複数の要素を取り出し、順番に並べるときに何通りの方法があるのか数えるのです。

樹形図や積の法則を理解していれば、順列の概念がわかります。また順列では階乗という言葉を学びます。階乗の概念は難しくないものの、順列を理解するためには階乗の記号や使い方を知っておく必要があります。

なお、順列の公式を知っていても問題をそれだけで解けることはありません。そのため応用問題を含めて、順列の公式を利用できるようになりましょう。

樹形図を理解しているのであれば、順列を簡単に理解できるはずです。ここでは、順列の公式や階乗の計算方法、問題の解き方を解説していきます。

順列の概念：樹形図と積の法則を利用する

既に全員が樹形図を学んでいると思います。何通りの方法があるのか数えるとき、樹形図を利用します。例えば1～3の数字が書かれている3枚のカードを利用し、3ケタの数字を作るとき何通りの方法があるでしょうか。

樹形図を利用すると、以下のようになります。

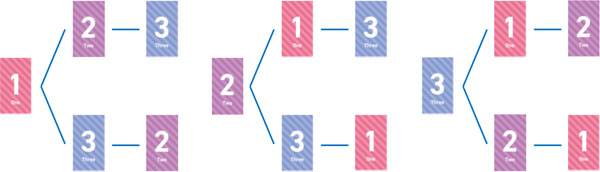
これにより、答えは6通りであるとわかります。また樹形図を利用しなくても、積の法則を利用することによって計算できます。

一番目に置ける数字の候補は3通りです。また一つの数字を使っているため、二番目に置ける数字の候補は2通りです。三番目に置ける数字については、すでに二つの数字を利用しているため、残った一つの数字を置くことになります。

そのため、以下のようにかけ算をすることで答えをだすことができます。

• 3通り × 2通り × 1通り ＝ 6通り

このように、樹形図なしにかけ算をすることで答えを出せることを積の法則といいます。

!を利用する階乗の記号

ここまでの内容を理解している場合、階乗を理解できるようになります。階乗では、左から順に並べるとき、何通りの方法があるのかを計算します。

先ほど、3枚のカードを利用することによって何通りの方法があるのか記しました。それでは、5枚のカードを作って5ケタの数字を作るとき、何通りの方法があるでしょうか。この場合、以下のようになります。

• \(5×4×3×2×1=120\)

重要なのは、利用できる数字（カード）が一つずつ減っている事実です。カードが5枚ある場合、最初は5通りの方法があり、二番目には4通りの方法があります。また、三番目には3通りの方法があります。こうして、利用できる数字が一つずつ減ります。利用した数字を再度使うことができないため、数字が一つずつ減るのです。

当然ながら、カードの枚数が増えても考え方は同じです。例えば8枚のカードを利用し、8ケタの数字を作る場合は以下の計算をします。

• \(8×7×6×5×4×3×2×1=40320\)

いずれにしても、順番に並べるときは積の法則を利用し、かけ算をする数字を一つずつ減らしていきます。このとき、階乗を利用します。階乗では!（エクスクラメーションマーク）を利用することによって表現します。階乗を利用するとき、以下のようになります。

• \(1!=1\)
• \(2!=2×1\)
• \(3!=3×2×1\)
• \(4!=4×3×2×1\)
• \(5!=5×4×3×2×1\)
• \(6!=6×5×4×3×2×1\)

数字に!を加えることによって、「一つずつ数字を減らしつつ、数が1になるまでかけ算をする」という意味になります。これが階乗です。

_nP_rの公式の意味と計算方法

ただ何通りの方法があるのか調べるとき、必ずしもすべてを並べるとは限りません。全候補の中で、一部を選んで順番に並べることがあります。

例えば1～6の数字が書かれた6枚のカードがあり、3つを利用して3ケタの数字を作るとき、何通りの方法があるでしょうか。この場合、最初は6通りの方法があります。また二番目は5通りの選択肢があり、三番目は4通りの選択肢があります。

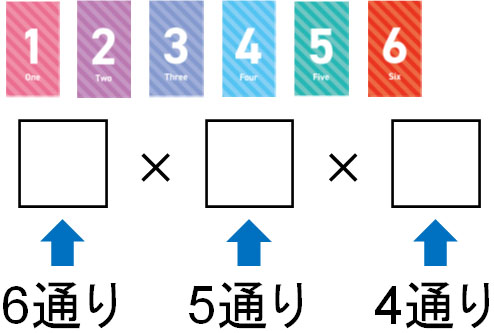
先ほどと同じように、最初はすべての選択肢があります。ただ、二番目や三番目では選べる候補が一つずつ減ります。また利用するカードは3枚なので、左から順に三番目までカードを配置してします。すべてのカードは使いません。

つまり階乗のように、全部の数字を利用して何通りの方法があるのか数えません。そうではなく特定の場所でストップし、何通りの方法があるのか数えます。これを考えるのが順列です。

順列ではPという記号を利用します。例えば、以下のようになります。

• \(_7P_4\)
• \(_{10}P_2\)
• \(_5P_3\)

₇P₄というのは、選択肢が7つある中から、4つを取り出して順番に並べることを意味します。また₁₀P₂というのは、選択肢が10つある中から、2つを取り出して順番に並べることを意味します。以下のような意味になります。

• \(_7P_4=7×6×5×4\)
• \(_{10}P_2=10×9\)
• \(_5P_3=5×4×3\)

先ほど、6枚あるカードの中から3つのカードを選び、左から順に並べる（3ケタの数字を作る）という例を解説しました。これは、選択肢が6つある中で3つを取り出し、順番に並べることを意味するので₆P₃と表すことができます。

これを順列の公式で記すと以下のようになります。

• \(_nP_r=\displaystyle\frac{n!}{(n-r)!}\)

n個の中からr個を取り出して一列に並べるとき、この公式を利用できます。ただ、おそらくこの公式を見てもまったく理解できないと思います。そこで公式を覚えるのではなく、₁₀P₂や₅P₃がどのようなかけ算になるのか理解しましょう。

ちなみに、例えば₄P₄は4!と意味が同じです。₄P₄は以下のように表すことができます。

• \(_4P_4=4×3×2×1= 4!\)

また、\(0!=1\)になることを理解しましょう。つまり、以下のようになります。

• \(_nP_0=0!=1\)

階乗というのは、前述のように「!の前に付けた数字について一つずつ数を減らしつつ、数が1になるまでかけ算をする」ことを表します。0!の場合、何もかけ算をしないので1と定義されます。そのため\(0!=1\)ですし、\(1!=1\)です。ただ\(2!\)の場合、\(2!=2×1\)になります。

順列の公式を利用する計算方法

それでは、順列の公式を利用して何通りの方法があるのか計算してみましょう。順列を利用する問題では、複数の解き方があります。

順列を利用するとき、最も簡単な計算は「全候補の中から選び、順番に並べる」ことです。ただ高校数学では、より複雑なケースについて、何通りの方法があるのか計算しなければいけません。例えば、以下のようなケースがあります。

• 順列を利用すると、条件を満たさないケースが発生する
• 特定の条件があるケース
• 特定の条件を除くケース

それぞれのケースについて、順列を利用して答えを出せるようにしましょう。

条件を満たさない場合は例外を省く

場合によっては、順列の公式を利用することによって条件を満たさないケースが発生します。例えば、以下の問題の答えは何でしょうか。

• 0～4の5枚のカードを利用して3ケタの数字を作るとき、何通りの方法があるでしょうか？

5枚のカードがあり、その中から3枚を選んで左から順に並べます。ただ、₅P₃を計算するのは間違いです。理由としては、必ず3ケタの数字を作る必要があるからです。要は、百の位に0を置くことはできません。

つまり、一番左に置ける数字は1～4のうちどれかです。その次に、2ケタの数字を作るときに0を利用することができます。十の位と一の位で2ケタの数字を作るとき、0を含む4つの候補の中から2つを選ぶことになります。そのため、2ケタの数字を作るときは₄P₂と表すことができます。

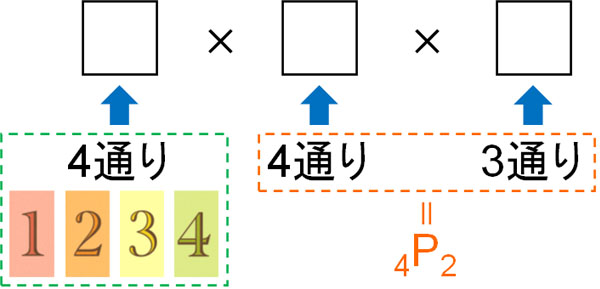
そのため、以下の計算式によって答えをだすことができます。

• \(4×_4P_2=4×4×3=48\)

こうして、48通りが答えであるとわかります。順列の公式を利用しても条件を満たさないことがあります。その場合、今回の例のように特定の条件下については順列の公式をそのまま利用せず、例外を省くように計算式を作りましょう。

特定の条件がある場合、それぞれ順列を計算する

なお、順列の計算問題で最も一般的なのは、特定の条件があるときに何通りの方法があるのか計算する問題です。例えば、以下の問題の答えは何でしょうか。

• A、B、C、D、Eの5人がいます。AとBが隣り合う場合、何通りの方法がありますか？

AとBは必ず隣り合う必要があります。そこで、AとBを一セットと考えましょう。そうすると、「A-B、C、D、E」の4つの順番を考えればいいことがわかります。つまり、4!（₄P₄）を計算しましょう。

ただAとBは入れ替えることができます。つまりA-BとB-Aのパターンがあります。AとBを並べるとき、2!通りの方法があります。

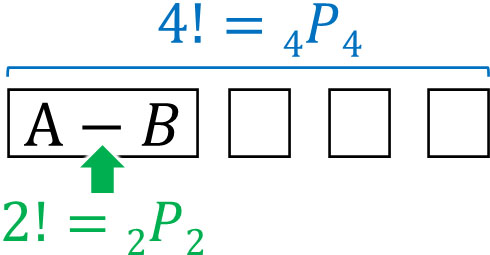
そのため、以下の式を解きましょう。

• \(4!×2!=4×3×2×2=48\)

こうして、48通りが答えであるとわかります。

なお特定の条件が与えられる問題については、多くのパターンに答えられるようにしましょう。例えば、以下の問題の答えは何でしょうか。

• A、B、C、D、Eの5人がいます。AとBが両端にくる場合、何通りの方法がありますか？

順列の問題を解くコツとしては、図を描くことがあります。先ほどの問題についても、図を描くと計算式を思いつきやすいです。両端にAとBがくる場合、以下のようになります。

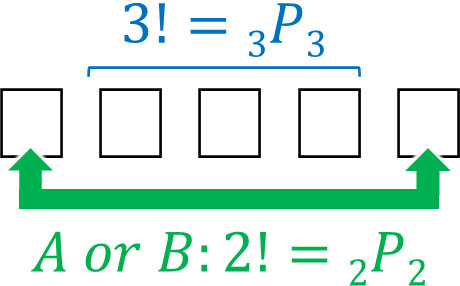
真ん中にC、D、Eを並べるとき、3!通りの方法があります。また両端は必ずAとBであるため、2!通りの方法があります。そのため、積の法則によって以下の計算式を作ることができます。

• \(3!×2!=3×2×2=12\)

こうして、答えは12通りであるとわかります。

特定の条件を省く場合、引き算によって答えをだす

場合によっては、特定の条件を除くこともあります。その場合、引き算を利用しましょう。例えば、以下の答えは何でしょうか。

• A、B、C、D、Eの5人がいます。BとCが隣り合わない場合、何通りの方法がありますか？

特定の条件を満たさないケースについては、全体から条件を満たすケースを引きましょう。例えば年間で「雨の日」を計算するとき、365日から「晴れの日」と「くもりの日」を引けば答えをだすことができます。同じように、全体から条件を満たすケースを引くと、条件を満たさないケースを求めることができるのです。

BとCが隣り合うケースについて、以下の計算によって答えをだすことができます（計算方法はすでに解説しています）。

• \(4!×2!=4×3×2×2=48\)

それでは、A、B、C、D、Eを並べるとき何通りの方法があるでしょうか。全体では5!通りあると計算できます。

• \(5!=5×4×3×2=120\)

全体が120通りであり、BとCが隣り合うのは48通りであるため、BとCが隣り合わないケースは96通りであるとわかります。

• \(120-48=72\)

それでは、次に少し複雑な問題を解いてみましょう。以下の答えは何でしょうか。

• A、B、C、D、Eの5人がいます。AとBが隣り合い、BとCが隣り合わない場合、何通りの方法がありますか？

この問題についても、全体から特定の条件を引くことによって答えをだしましょう。先ほどの計算より、AとBが隣り合うケースは48通りです。そこで48から、「AとBが隣り合い、かつBとCが隣り合う場合」を除きましょう。そうすれば、AとBが隣り合い、BとCが隣り合わない場合を計算できます。

AとBが隣り合い、かつBとCが隣り合う場合というのは、A-B-CまたはC-B-Aの並び順になっていることを意味します。そこでA-B-Cを一セットとみなすと、以下の図を作ることができます。

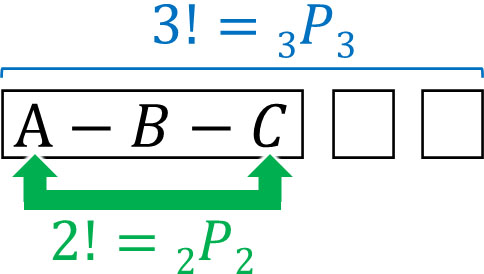
A-B-Cが一セットの場合、3!通りの並べかたがあります。またBは固定されており、AとCは移動させることができます。そのため、2!通りの方法があります。そのため積の法則により、AとBが隣り合い、BとCが隣り合うケースは12通りです。

• \(3!×2!=3×2×2=12\)

全体は48通りであるため、AとBが隣り合い、BとCが隣り合わない場合は36通りです。

• \(48-12=36\)

このように特定の条件を除くとき、引き算をすることによって何通りの方法があるのか数えることができます。

階乗の意味を理解し、順列の公式を利用する

順列では順番を意識しましょう。どのような順番で並ばせるのかについて、何通りの方法があるのか数えるのが順列です。そこで順列を理解するため、樹形図や積の法則、階乗の意味を理解しましょう。

階乗を学べば、順列を理解できます。階乗ではすべての候補を利用して並べるとき、何通りの方法があるのか数えます。一方で順列では、全体の中から一部の候補を利用して並べるときに何通りの方法があるのか調べることができます。

なお順列の公式を利用するとき、条件を満たさないケースがあったり、特定の条件が与えられていたりします。引き算を利用して何通りあるのか答えなければいけないこともあります。そこで、さまざまなパターンの問題を解けるようにしましょう。

順列の公式を覚えても理解は難しいです。そこで実際の例を確認し、問題のパターンを把握して、順列の問題を解きましょう。