三角比で利用される公式として正弦定理と余弦定理があります。三角比を利用することによって、辺の長さ(または三角比の値)を求められる公式が正弦定理と余弦定理です。
正弦定理と余弦定理は「わからない辺の長さや角度を計算できる」という点では同じです。ただ、使用する場面が異なります。正弦定理を利用するべき計算があれば、余弦定理を利用して計算するべき場面もあるのです。
これらの公式を理解した後、三角形での辺と角の大小関係を学べば、例えば鋭角三角形になる条件を計算することができます。
辺の長さや角度を計算するのは、力学や土木など多くの場面で利用されます。そのため、正弦定理と余弦定理は重要な公式の一つになります。
もくじ
三角形は必ず外接円をもつ
まず、三角形の性質を理解しましょう。三角形には多くの性質があり、その一つが外接円をもつことです。つまり、すべての三角形で外接円を描くことができます。
外接円とは、三角形の外で接する以下のような円を指します。
なぜ外接円を理解する必要があるかというと、正弦定理で利用されるからです。なお正弦定理と余弦定理は証明することができるものの、公式を覚えてしまうようにしましょう。
数学には覚えるべき公式と覚えなくてもいい公式があります。正弦定理と余弦定理は覚えなければいけない公式です。
正弦定理により、sinθで辺の長さや角度、外接円の半径がわかる
それでは、正弦定理の公式はどのようになっているのでしょうか。正弦定理では、以下のような辺と角度、半径(R)をもつ三角形と外接円を考えます。
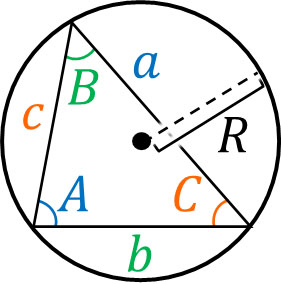
三角形の形はどのようなものであってもいいです。ひとまず、このような三角形を考えるのです。そうすると、以下の公式が成り立ちます。
- \(\displaystyle\frac{a}{sinA}=\displaystyle\frac{b}{sinB}=\displaystyle\frac{c}{sinC}=2R\)
これが正弦定理です。角度と辺の長さを利用することによって、ほかの辺の長さや外接円の半径を求めることができるのです。sine(正弦:sin)を利用する公式であるため正弦定理と呼ばれています。
・正弦定理を利用して計算する
それでは、実際に正弦定理を利用してみましょう。以下の三角形で\(a\)と外接円の半径を求めましょう。
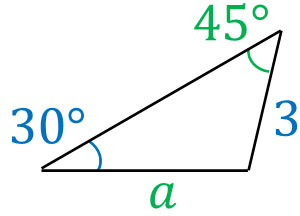
先ほど解説した正弦定理を利用して、辺の長さを出しましょう。以下の式を作ることができます。
- \(\displaystyle\frac{3}{sin30°}=\displaystyle\frac{a}{sin45°}\)
この式を解きます。
\(\displaystyle\frac{3}{sin30°}=\displaystyle\frac{a}{sin45°}\)
\(3÷\displaystyle\frac{1}{2}=a÷\displaystyle\frac{1}{\sqrt{2}}\)
\(3×2=a×\sqrt{2}\)
\(a=\displaystyle\frac{6}{\sqrt{2}}\)
\(a=3\sqrt{2}\)
また外接円の半径についても正弦定理を利用することで求めることができます。以下の式を作りましょう。
- \(\displaystyle\frac{3}{sin30°}=2R\)
この式を解きます。
\(\displaystyle\frac{3}{sin30°}=2R\)
\(3×2=2R\)
\(3=R\)
こうして、正弦定理を利用することによって辺の長さや外接円の半径を計算できるようになります。また、sinθの値から角度を求めることもできます。
余弦定理により、cosθで辺の長さを出す
一方でcosine(余弦:cos)を利用する公式もあります。それが余弦定理です。余弦定理では、外接円の半径を求めることはできません。その代わり、辺の長さと角度を計算することができます。
例えば、以下の三角形があるとします。
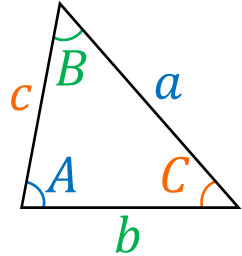
このとき、以下の公式が余弦定理です。
- \(a^2=b^2+c^2-2bccosA\)
- \(b^2=c^2+a^2-2cacosB\)
- \(c^2=a^2+b^2-2abcosC\)
覚え方としては、「2辺とその間の角を利用して、角の対辺を計算する」と理解しましょう。三角形の合同条件に「2辺のその間の角が等しい」があります。これを利用して余弦定理を覚えるのです。
・余弦定理を利用して計算する
それでは、実際に余弦定理を利用して計算してみましょう。以下の三角形で\(a\)の値は何でしょうか。
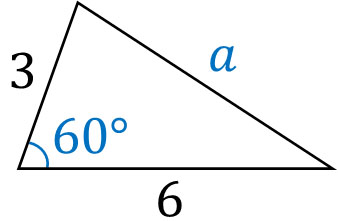
\(a^2=b^2+c^2-2bccosA\)を利用して、\(a\)の値を見つけましょう。以下のようになります。
\(a^2=3^2+6^2-2×3×6×cos60°\)
\(a^2=9+36-2×3×6×\displaystyle\frac{1}{2}\)
\(a^2=45-18\)
\(a^2=27\)
\(a=±3\sqrt{3}\)
\(a\)は辺の長さであるため、\(a>0\)です。そのため、\(a=3\sqrt{3}\)が正解です。
正弦定理と余弦定理の使い分け
正弦定理でも余弦定理でも、辺の長さと角度を求めることができます。それでは、どのように正弦定理と余弦定理を使い分ければいいのでしょうか。
三角形の合同条件では以下が利用されます。
- 一辺とその両端の角が等しい
- 二辺とその間の角が等しい
- 三辺がそれぞれ等しい
この合同条件を満たすことによって、三角形の形が決まります。正弦定理と余弦定理の使い分けでは、三角形の合同条件を利用して以下のように覚えましょう。
- 一つの辺と2つの角度がわかっている:正弦定理を利用
- 二つの辺と1つの角度がわかっている:余弦定理を利用
- 三つの辺の長さがわかっている:余弦定理を利用
正弦定理を利用するとき、一辺とその両端の角がわかっている必要はありません。両端の角ではなく、その他の角度がわかっていれば正弦定理を利用できます。先ほど以下の三角形について、正弦定理を利用して\(a\)の値を計算しました。

このように、一つの辺と2つの角度がわかっていればいいのです。
同じように余弦定理でも、二つの辺と1つの角度がわかっている場合であれば利用できます。また三つの辺がわかっている場合、必ず余弦定理を利用して角度をだしましょう。
・二つの辺と1つの角度がわかっている
なお二つの辺と1つの角度がわかっている場合、正弦定理を利用することによっても辺の長さや角度を計算することができます。それにも関わらず、なぜ余弦定理を利用するのでしょうか。先ほど、余弦定理を利用して計算した以下の三角形で考えてみましょう。
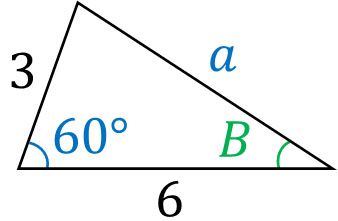
余弦定理を利用する場合、一つの答えが出ます。一方で正弦定理では、二つの答えの候補を得られます。そのため、どちらの答えが正しいのか確認しなければいけません。つまり、計算ミスが起こりやすいのです。
先ほど余弦定理を利用した計算結果より、\(a=3\sqrt{3}\)です。それでは、∠Bの大きさは何度でしょうか。余弦定理を利用する場合、以下のように計算できます。
\(3^2=6^2+(3\sqrt{3})^2-2×6×3\sqrt{3}×cosB\)
\(9=36+27-36\sqrt{3}cosB\)
\(36\sqrt{3}cosB=54\)
\(cosB=\displaystyle\frac{54}{36\sqrt{3}}\)
\(cosB=\displaystyle\frac{54×\sqrt{3}}{36×3}\)
\(cosB=\displaystyle\frac{\sqrt{3}}{2}\)
こうして、\(cosB=\displaystyle\frac{\sqrt{3}}{2}\)となります。これを満たすためには、\(B=30°\)でなければいけません。こうして、角度を計算できます。
・正弦定理では答えの候補が2つ出る
一方で正弦定理を利用する場合、答えの候補が2つ出ます。以下のように、正弦定理で計算してみましょう。
\(\displaystyle\frac{3}{sinB}=\displaystyle\frac{3\sqrt{3}}{sin60°}\)
\(\displaystyle\frac{3}{sinB}=3\sqrt{3}÷sin60°\)
\(\displaystyle\frac{3}{sinB}=3\sqrt{3}÷\displaystyle\frac{\sqrt{3}}{2}\)
\(\displaystyle\frac{3}{sinB}=3\sqrt{3}×\displaystyle\frac{2}{\sqrt{3}}\)
\(\displaystyle\frac{3}{sinB}=6\)
\(sinB=\displaystyle\frac{1}{2}\)
こうして、\(sinB=\displaystyle\frac{1}{2}\)と計算できます。\(sinB=\displaystyle\frac{1}{2}\)を満たす角度としては30°と150°があります。このように正弦定理を利用すると2つの角度が出てきます。
ただ一つの角度は60°と決まっています。もし∠Bが150°の場合、2つの角度を足すと210°になります。三角形の内閣の和は必ず180°になるため、∠Bが150°になることはありません。そのため、∠Bは30°であるとわかります。
正弦定理であっても角度を計算することができます。ただ答えの候補が2つ出てくるため、二辺と1つの角度がわかっている場合、正弦定理ではなく余弦定理を利用しましょう。
辺の長さと角の大小関係
ここまでの内容を理解した後、三角形の角度の大きさを理解しましょう。感覚的にわかると思いますが、三角形で角度が大きい場合、その対辺は長くなります。一方で角度が小さい場合、対辺の長さは短いです。
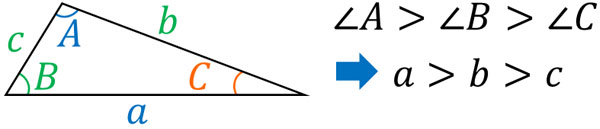
この性質を利用して問題を解いてみましょう。例えば、△ABCで\(\displaystyle\frac{\sqrt{3}}{sinA}\)\(=\displaystyle\frac{\sqrt{7}}{sinB}\)\(=\displaystyle\frac{1}{sinC}\)が成り立つとき、最も大きい角度は何度でしょうか。
正弦定理より、\(a:b:c\)\(=sinA:sinB:sinc\)\(=\sqrt{3}:\sqrt{7}:1\)になります。つまり、以下のようになります。
- \(\displaystyle\frac{a}{\sqrt{3}}\)\(=\displaystyle\frac{b}{\sqrt{7}}\)\(=\displaystyle\frac{c}{1}=k(k>0)\)
これにより、\(a=\sqrt{3}k\)、\(b=\sqrt{7}k\)、\(c=k\)となります。また最も大きい角度では、その対辺の長さが最も大きくなります。そこで辺の長さを比べると、\(b\)の長さが最も大きいです。つまり、最も大きい角度は∠Bです。
そこで、余弦定理を利用して角度を計算しましょう。以下のようになります。
\(b^2=c^2+a^2-2cacosB\)
代入すると
\((\sqrt{7}k)^2=(\sqrt{3}k)^2+k^2-2×\sqrt{3}k×k×cosB\)
\(7k^2=3k^2+k^2-2\sqrt{3}k^2cosB\)
\(2\sqrt{3}k^2cosB=-3k^2\)
\(2\sqrt{3}cosB=-3\)
\(cosB=-\displaystyle\frac{3}{2\sqrt{3}}\)
\(cosB=-\displaystyle\frac{\sqrt{3}}{2}\)
\(cosB=-\displaystyle\frac{\sqrt{3}}{2}\)となるのは、∠Bが150°のときです。そのため、最大の角度は150°であるとわかります。
正弦定理と余弦定理の公式を覚える
重要な公式が正弦定理と余弦定理です。公式を覚える必要はあるものの、公式を利用することによって三角形の辺や角度を計算することができます。
辺や角度を計算できるという意味では、正弦定理と余弦定理は似ています。ただ、利用する場面が異なります。一辺の長さと2つの角度がわかっている場合、正弦定理を利用しましょう。外接円の半径を出したいときについても正弦定理が有効です。
一方で二辺の長さと1つの角度がわかっている場合、余弦定理を利用しましょう。三辺の長さがわかっているときも余弦定理を使います。
sinθとcosθを利用することによって、どのように辺の長さと角度の大きさを計算すればいいのか理解しましょう。






