二次方程式を解く場合、必ずしも答えを得られるとは限りません。解なしのケースがあります。ただ虚数を学んだあとでは、解を得られるようになります。
言い換えると、虚数を用いて答えを出すことができます。複素数が重要なのは、それまで答えを得られないケースであっても、明確な答えを得られるからです。
答えがない場合、明確な数字を得ることができません。一方で複素数を利用すれば、明確な数字を得ることができます。複素数を学ぶ必要があるのは、明確な答えを得ることができて便利だからです。そこで、二次方程式で虚数解を得られる条件や判別式の性質を学びましょう。
それでは、どのようなときに二次方程式で虚数解を得られるのでしょうか。二次方程式での複素数の関係や計算方法を解説していきます。
もくじ
二次方程式で虚数解をもつケース
二次方程式で虚数解をもつ場合、どのような答えになるのでしょうか。二次方程式を解く場合、因数分解、または解の公式を利用します。
なお虚数解をもつ二次方程式では、以下の解の公式を利用します。
$$x={-b\pm\sqrt{b^2-4ac}\over2a}$$
それでは、以下の問題の答えは何でしょうか。
- \(x^2+x+1=0\)
複素数を学ぶ前であれば、答えは解なしです。一方で複素数を学んだあとであれば、明確な答えを得ることができます。以下のように計算しましょう。
\(x=\displaystyle\frac{-1±\sqrt{1-4}}{2}\)
\(x=\displaystyle\frac{-1±\sqrt{-3}}{2}\)
\(x=\displaystyle\frac{-1±\sqrt{3}i}{2}\)
こうして、答えは\(x=\displaystyle\frac{-1±\sqrt{3}i}{2}\)となります。答えは解なしではなく、虚数\(i\)を含む答えとなるのです。
判別式と虚数解の判断
それでは、どのようなときに虚数解を得られるのでしょうか。二次方程式では判別式\(D\)を利用します。判別式\(D\)の値がプラス、0、マイナスによって、解が存在するかどうかを確認できます。
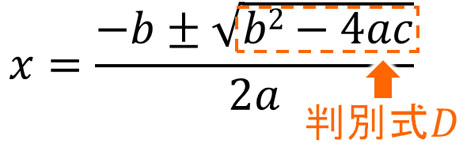
そこで複素数を学んだあとでは、以下のように考えましょう。
- 判別式\(D\)が正の値:2つの実数解をもつ
- 判別式\(D\)が0:1つの実数解をもつ(重解)
- 判別式\(D\)が負の値:2つの虚数解をもつ
\(\sqrt{-1}=i\)であるため、判別式\(D\)がマイナスになる場合、虚数を利用して解を得ることができます。
判別式を用いる虚数解の条件
それでは、虚数解をもつ二次方程式に関する問題を解いてみましょう。以下の問題の答えは何でしょうか。
- \(x^2+kx+k=0\)と\(x^2+(k+1)x+4\)の両方とも虚数解となる定数\(k\)の範囲を求めましょう。
両方とも虚数解となればいいため、判別式が両方とも\(D<0\)となる定数\(k\)の範囲を計算しましょう。
・\(x^2+kx+k=0\)の判別式
\(k^2-4k<0\)
\(k(k-4)<0\)
\(0<k<4\)
・\(x^2+(k+1)x+4\)の判別式
\((k+1)^2-16<0\)
\(k^2+2k-15<0\)
\((k-3)(k+5)<0\)
\(-5<k<3\)
\(0<k<4\)と\(-5<k<3\)の両方を満たす必要があるため、答えは\(0<k<3\)であるとわかります。
係数に虚数を含む二次方程式の解の出し方
次に、係数に虚数を含む場合の解の出し方を学びましょう。判別式\(D\)を利用するとき、係数は必ず実数でなければいけません。係数に虚数を含む場合、判別式を使用できません。
例えば、以下の式は判別式を利用できません。
- \((1-i)x^2-(k-i)x+1+ki=0\)
それでは、この式が実数解をもつ場合、定数\(k\)の値を得るにはどうすればいいのでしょうか。係数に虚数を含む場合、判別式を利用せずに計算しましょう。具体的には、実数解を\(x=α\)とします。その後、虚数\(i\)を基準に整理しましょう。以下のように計算します。
\((1-i)α^2-(k+i)α+1+ki=0\)
\((α^2-kα+1)-(α^2+α-k)i=0\)
\(α\)と\(k\)は実数であるため、\(α^2-kα+1\)と\(α^2+α-k\)も実数です。そのため\((α^2-kα+1)-(α^2+α-k)i=0\)を満たすためには、以下の2つの条件を満たす必要があります。
- \(α^2-kα+1=0\) – ①
- \(α^2+α-k=0\) – ②
\(②-①\)より、以下のように計算しましょう。
\(α+kα-k-1=0\)
\((1+k)α-(1+k)=0\)
\((1+k)(α-1)=0\)
そのため、\(k=-1\)または\(α=1\)となります。
・\(k=-1\)の場合
①と②は両方とも\(α^2+α+1=0\)となります。ただ\(α^2+α+1=0\)に対して判別式\(D\)を利用すると、\(D=1-4=-3\)となり、\(α\)は実数解をもたないことがわかります。「\(α\)は実数解である」という条件に合わないため、\(k=-1\)は不適です。
・\(α=1\)の場合
\(α=1\)の場合、①と②の両方とも\(k=2\)です。\(α\)と\(k\)は両方とも実数であるため、条件を満たします。つまり\(k=2\)が正解であり、このときの実数解は1です。
純虚数解をもつ場合の計算方法
次に、純虚数解をもつ場合の計算方法を学びましょう。考え方は先ほどと同じであるものの、答えの設定方法が異なります。
実際に練習問題を解くことで学びましょう。以下の式について、純虚数解をもつ定数\(k\)を求めましょう。
- \((1-i)x^2-(k+3i)x-2+ki=0\)
純虚数解を\(x=αi\)とします。なお、\(α\)は実数です。\(α\)が実数であれば、\(αi\)は必ず純虚数解となります。そこで、以下のように\(x=αi\)を代入して計算しましょう。
\((1-i)α^2i^2-(k+3i)αi-2+ki=0\)
\((-α^2+3α-2)+(α^2-kα+k)i=0\)
\(α\)と\(k\)は実数であるため、\(-α^2+3α-2\)と\(α^2-kα+k\)も実数です。そのため\((-α^2+3α-2)+(α^2-kα+k)i=0\)を満たすためには、以下の2つの条件を満たす必要があります。
- \(-α^2+3α-2=0\) – ①
- \(α^2-kα+k=0\) – ②
①より、以下のように計算しましょう。
\(-α^2+3α-2=0\)
\(α^2-3α+2=0\)
\((α-2)(α-1)=0\)
\(α=1\)または\(α=2\)
・\(α=1\)のとき
\(α^2-kα+k=0\)
\(1-k+k=0\)
この式を満たす\(k\)は存在しないため、\(α=1\)は不適です。
・\(α=2\)のとき
\(α^2-kα+k=0\)
\(4-2k+k=0\)
\(k=4\)
\(α=2\)と\(k=4\)は両方とも実数であり、条件を満たします。そのため答えは\(k=4\)であり、このときの純虚数解は\(2i\)です。
複素数を利用して二次方程式の虚数解を得る
二次方程式では、解がある場合とない場合を学びます。ただ複素数を学んだあとでは、すべての二次方程式で解をもつようになります。そこで、どのようなときに虚数解を得られるのか理解しましょう。
判別式\(D\)を利用することにより、実数解をもつのか、それとも虚数解をもつのか判断できます。具体的な値を得たい場合、解の公式を利用することによって虚数解を計算しましょう。
なお係数に虚数を含む場合、判別式を利用できません。この場合、複素数の性質を利用することによって答えを得るようにしましょう。実数と虚数を使い分け、すべての条件を満たす値を計算によって得るのです。
すべての二次方程式について、虚数を利用することで明確な答えを得られます。そこで複素数の性質を利用し、答えを導き出せるようになりましょう。






