漸化式が関わる問題に確率があります。確率漸化式は内容が非常に難しく、問題の解き方を知らないと答えを得ることができません。
また、そもそも確率漸化式に関する問題であることを見極める必要があります。反復試行の確率と確率漸化式を区別できるようになりましょう。
なお確率漸化式では、複数の事象を考慮する必要があったり、隣接3項の漸化式を利用したりするケースがあります。これらの確率漸化式についても、式を作ることによって答えを得られるようになりましょう。
それでは、確率漸化式の問題を解くにはどのようにすればいいのでしょうか。確率漸化式の見極め方や式の作り方、問題の解き方を解説していきます。
もくじ
反復試行の確率と確率漸化式の見極め方
確率漸化式の問題が難しい理由としては、そもそも「確率漸化式を利用して問題を解かなければいけないのかどうかわからない」ことがあげられます。似た確率の問題に反復試行の確率があります。反復試行の確率では以下のような問題文になります。
- サイコロを5回投げ、1の目が2回出る確率を求めましょう。
この場合、以下のように計算します。
- \(_5C_2\left(\displaystyle\frac{1}{6}\right)^2\left(\displaystyle\frac{5}{6}\right)^3=\displaystyle\frac{625}{3888}\)
このように反復試行の確率では、\(n\)回のイベントのうち、目的の事象が何回起こるのか決まっています。
一方で確率漸化式では、\(n\)回のイベントのうち、目的の事象がいつ、何回起こるのか決まっていません。そのため、以下のような問題文になります。
- サイコロを\(n\)回投げ、1の目が奇数回出る確率を求めましょう。
「サイコロを\(n\)回投げ、1の目が10回出る」という場合、反復試行の確率です。ただサイコロを\(n\)回投げるとき、1の目がいつ、何回出るのか問題文を読んでも不明です。奇数回は3回かもしれないし、7回かもしれません。この場合、確率漸化式を利用します。目的とする事象の回数が明確にわかるかどうかを基準に判断しましょう。
確率漸化式の解き方と方針
それでは、どのように考えて確率漸化式の問題を解けばいいのでしょうか。漸化式では、以前の結果を利用して次の結果の得ることができます。そこで、\(n\)回目と\(n+1\)回目に着目しましょう。
確率漸化式では、\(n\)回目に事象が起こる確率を\(P_n\)とします。また、\(n+1\)回目に事象が起こる確率を\(P_{n+1}\)とします。そうして、以下の式を作ります。
- \(P_{n+1}=a·P_n+b\)
つまり、\(n\)回目に事象が起こる確率\(P_n\)を利用して、\(n+1\)回目に目的の事象が起こる確率\(P_{n+1}\)を式で表しましょう。このような漸化式を作れば、特性方程式を利用することによって一般項を得られます。これが、確率漸化式の大まかな方針です。
漸化式を作るとき、目的の事象が\(n+1\)回目に起こるときの確率を式として表すのが特徴です。\(n\)回目に事象が起こる確率\(P_n\)はわからないため、\(P_n\)を利用して\(P_{n+1}\)を表すのです。
なお\(n+1\)回目に目的とする事象Mが起こる確率\(P_{n+1}\)を計算するとき、以下の2パターンで考える必要があります。
- \(n\)回目に事象Mが起こり、\(n+1\)回目も事象Mが起こる
- \(n\)回目に事象Mが起こらず、\(n+1\)回目に事象Mが起こる
なお、\(n\)回目に事象Mが起こる確率が\(P_n\)なのであれば、\(n\)回目に事象Mが起こらない確率は\(1-P_n\)です。
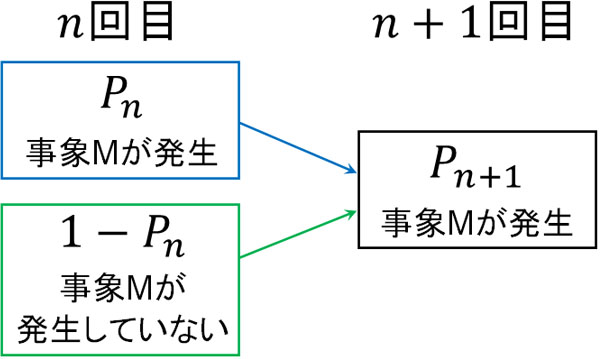
こうした関係を利用することにより、\(n+1\)回目に事象Mが起こる確率を計算します。
隣接2項間の漸化式での練習問題
それでは、実際に問題を解くことによって確率漸化式を学びましょう。以下の問題の答えは何でしょうか。
- サイコロを\(n\)回投げ、1の目が奇数回出る確率を求めましょう。
サイコロを\(n\)回投げるとき、1の目がいつ、何回出るのかは決められていません。この場合、反復試行の確率ではなく確率漸化式を利用します。
前述の通り、確率漸化式では\(n+1\)回目に目的の事象を得られる確率を式に表します。サイコロを\(n+1\)回投げるとき、1の目が奇数回出るとき、以下のケースが考えられます。
- \(n\)回目に1の目が奇数回出ており、\(n+1\)回目に1の目以外が出る
- \(n\)回目に1の目が偶数回出ており、\(n+1\)回目に1の目が出る
なお、上記2つが同時に起こることはありません。そのため、両方の確率を足すことによって\(n+1\)回目に1の目が奇数回出る確率を得ることができます。
サイコロを投げ、\(n\)回目に1の目が奇数回出る確率を\(P_n\)とします。1の目以外が出る確率は\(\displaystyle\frac{5}{6}\)であるため、「\(n\)回目に1の目が奇数回出ており、\(n+1\)回目に1の目以外が出る確率」は以下のようになります。
- \(P_n×\displaystyle\frac{5}{6}\)
またサイコロを投げ、1の目が出る確率は\(\displaystyle\frac{1}{6}\)です。そのため、「\(n\)回目に1の目が偶数回出ており、\(n+1\)回目に1の目が出る確率」は以下のようになります。
- \((1-P_n)×\displaystyle\frac{1}{6}\)
こうして、以下の漸化式を作ることができます。
\(P_{n+1}=\displaystyle\frac{5}{6}P_n\)\(+(1-P_n)\displaystyle\frac{1}{6}\)
\(P_{n+1}=\displaystyle\frac{2}{3}P_n+\displaystyle\frac{1}{6}\)
漸化式を作ることができれば、特性方程式を利用して問題を解けばいいです。以下のように計算しましょう。
\(α=\displaystyle\frac{2}{3}α+\displaystyle\frac{1}{6}\)
\(\displaystyle\frac{1}{3}α=\displaystyle\frac{1}{6}\)
\(α=\displaystyle\frac{1}{2}\)
そのため、以下の式を作れます。
- \(P_{n+1}-\displaystyle\frac{1}{2}=\displaystyle\frac{2}{3}\left(P_n-\displaystyle\frac{1}{2}\right)\)
サイコロを一回投げ、1の目が出る確率\(P_1\)は\(\displaystyle\frac{1}{6}\)です。数列\(\left\{P_n-\displaystyle\frac{1}{2}\right\}\)は初項\(P_1-\displaystyle\frac{1}{2}=-\displaystyle\frac{1}{3}\)、公比\(\displaystyle\frac{2}{3}\)の等比数列です。そのため、以下の式を作れます。
\(P_n-\displaystyle\frac{1}{2}=-\displaystyle\frac{1}{3}·\left(\displaystyle\frac{2}{3}\right)^{n-1}\)
\(P_n=-\displaystyle\frac{2^{n-1}}{3^n}+\displaystyle\frac{1}{2}\)
こうして、\(P_n\)を計算することができました。確率漸化式の計算方法を理解していないと問題を解くのは不可能なほど難しいです。そこでどのように式を作り、計算すればいいのか学びましょう。
同じ要素とみなせる場合、一つの文字で確率を表す
先ほど、2つの事象(1の目と1以外の目)について確認しました。ただ確率漸化式では、複数の事象を取り扱うケースがあります。この場合、2つや3つの事象について、同じ要素とみなせるかどうか確認しましょう。
それでは、以下の問題の答えは何でしょうか。
- △ABCの各頂点を移動する点Pがあります。点Pは1秒ごとに、\(\displaystyle\frac{1}{2}\)の確率で頂点にとどまり、\(\displaystyle\frac{1}{4}\)の確率でほかの頂点へそれぞれ移動します。最初、点Pが頂点Aに存在する場合、\(n\)秒後に点Pが頂点Aにある確率を計算しましょう。
いつ、何回、点Pが頂点Aに存在するのか不明です。そのため、確率漸化式を用いて計算しましょう。そこで、以下の場面を想定します。
- \(n\)秒後に点Pが頂点Aに存在し、\(n+1\)秒後に点Pが頂点Aにある。
- \(n\)秒後に点Pが頂点Bに存在し、\(n+1\)秒後に点Pが頂点Aに移動する。
- \(n\)秒後に点Pが頂点Cに存在し、\(n+1\)秒後に点Pが頂点Aに移動する。
\(n\)秒後に点Pが頂点A、頂点B、頂点Cに存在する確率をそれぞれ\(a_n\)、\(b_n\)、\(c_n\)とします。このとき、\(n+1\)秒後に点Pが頂点Aに存在する確率は以下のように表せます。
\(a_{n+1}=\displaystyle\frac{1}{2}a_n+\displaystyle\frac{1}{4}b_n+\displaystyle\frac{1}{4}c_n\)
\(a_{n+1}=\displaystyle\frac{1}{2}a_n+\displaystyle\frac{1}{4}(b_n+c_n)\)
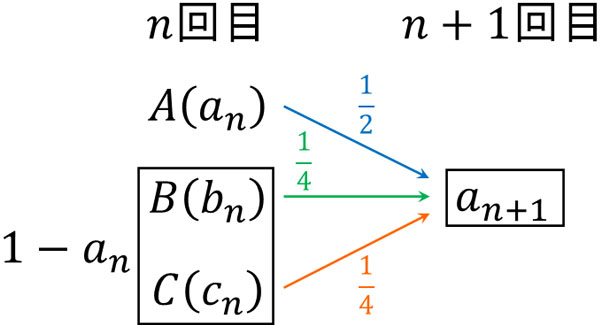
\(b_n\)から\(a_{n+1}\)になるときと、\(c_n\)から\(a_{n+1}\)になるときとの確率は両方とも\(\displaystyle\frac{1}{4}\)で共通です。
またすべての確率を足すと必ず1になるため、\(b_n+c_n=1-a_n\)です。そこで、先ほど計算した式に\(b_n+c_n=1-a_n\)を代入しましょう。
\(a_{n+1}=\displaystyle\frac{1}{2}a_n+\displaystyle\frac{1}{4}(b_n+c_n)\)
\(a_{n+1}=\displaystyle\frac{1}{2}a_n+\displaystyle\frac{1}{4}(1-a_n)\)
\(a_{n+1}=\displaystyle\frac{1}{4}a_n+\displaystyle\frac{1}{4}\)
こうして、\(a_n\)のみの式で表すことができました。複数の事象が存在する場合、今回の計算のように、まとめることができないか考えましょう。なお、特性方程式を利用して計算すると以下のようになります。
\(α=\displaystyle\frac{1}{4}α+\displaystyle\frac{1}{4}\)
\(\displaystyle\frac{3}{4}α=\displaystyle\frac{1}{4}\)
\(α=\displaystyle\frac{1}{3}\)
\(α=\displaystyle\frac{1}{3}\)であるため、以下の漸化式へ変形できます。
- \(a_{n+1}-\displaystyle\frac{1}{3}=\displaystyle\frac{1}{4}\left(a_n-\displaystyle\frac{1}{3}\right)\)
点Pは\(\displaystyle\frac{1}{2}\)の確率で同じ場所にとどまるため、1秒後に点Pが頂点Aに存在する確率は\(a_1=\displaystyle\frac{1}{2}\)です。そのため、数列\(\left\{a_n-\displaystyle\frac{1}{3}\right\}\)は初項\(a_1-\displaystyle\frac{1}{3}=\displaystyle\frac{1}{6}\)、公比\(\displaystyle\frac{1}{4}\)の等比数列です。そのため、以下の式を作れます。
\(a_n-\displaystyle\frac{1}{3}=\displaystyle\frac{1}{6}·\left(\displaystyle\frac{1}{4}\right)^{n-1}\)
\(a_n=\displaystyle\frac{1}{6}·\left(\displaystyle\frac{1}{4}\right)^{n-1}+\displaystyle\frac{1}{3}\)
こうして、\(n\)秒後に点Pが頂点Aに存在する確率を得ることができました。
隣接3項間の確率漸化式
確率漸化式の応用問題では、隣接3項間の漸化式が関わる問題が出題されます。そこで、隣接3項間の漸化式を作ることで答えを得られるようになりましょう。以下の問題の答えは何でしょうか。
- 数直線上の原点Oを出発点とします。コインを投げ、表が出たら2、裏が出たら1、正の方向へ進みます。また、点\(n\)に到達する確率を\(p_n\)とし、\(n\)は自然数です。3以上の\(n\)について、\(p_n\)、\(p_{n-1}\)、\(p_{n-2}\)の関係式を表し、\(p_n\)を求めましょう。
コインを何回投げるのか決められていません。そこで、確率漸化式を用いて計算しましょう。コインが点\(n\)に到達する場合、以下の2通りが存在します。
- 点\(n-2\)に到達後、コインを投げて表が出る。
- 点\(n-1\)に到達後、コインを投げて裏が出る。
数直線上で点\(n-2\)に存在する場合、表が出れば2進むことで点\(n\)に到達します。表が出る確率は\(\displaystyle\frac{1}{2}\)であるため、点\(n-2\)に到達する確率を\(p_{n-2}\)とすると、点\(n\)に到達する確率を\(\displaystyle\frac{1}{2}p_{n-2}\)と表すことができます。
また数直線上で点\(n-1\)に存在する場合、裏が出れば1進むことで点\(n\)に到達します。裏が出る確率は\(\displaystyle\frac{1}{2}\)であるため、点\(n-1\)に到達する確率を\(p_{n-1}\)とすると、点\(n\)に到達する確率を\(\displaystyle\frac{1}{2}p_{n-1}\)と表すことができます。
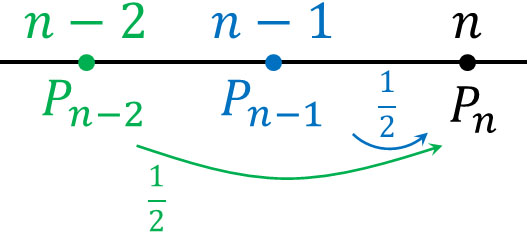
なお、その他の方法によって点\(n\)に到達する方法はありません。また、\(p_{n-2}\)と\(p_{n-1}\)が同時に起こることはありません。そのため、以下のように\(p_n\)を記すことができます。
- \(p_n=\displaystyle\frac{1}{2}p_{n-1}+\displaystyle\frac{1}{2}p_{n-2}\)
こうして、隣接3項間の漸化式を作ることができました。
なお、点1に到達する確率\(p_1\)は\(\displaystyle\frac{1}{2}\)です。裏が1回出れば、点1に到達できます。一方、点2に到達する確率\(p_2\)は「表1回」または「裏2回」が出る確率を足せばいいため、\(p_2=\displaystyle\frac{1}{2}+\displaystyle\frac{1}{2}·\displaystyle\frac{1}{2}\)\(=\displaystyle\frac{3}{4}\)です。
それでは、特性方程式を利用して隣接3項間の漸化式を変形しましょう。
\(x^2=\displaystyle\frac{1}{2}x+\displaystyle\frac{1}{2}\)
\(2x^2-x-1=0\)
\((2x+1)(x-1)=0\)
こうして、\(x=-\displaystyle\frac{1}{2},1\)とわかりました。そのため、以下の漸化式へ変形できます。
- \(p_n-p_{n-1}=-\displaystyle\frac{1}{2}(p_{n-1}-p_{n-2})\)
- \(p_n+\displaystyle\frac{1}{2}p_{n-1}=p_{n-1}+\displaystyle\frac{1}{2}p_{n-2}\)
\(p_n-p_{n-1}=-\displaystyle\frac{1}{2}(p_{n-1}-p_{n-2})\)に着目しましょう。数列\(\{p_{n+1}-p_{n}\}\)は初項\(p_{2}-p_{1}=\displaystyle\frac{1}{4}\)、公比\(-\displaystyle\frac{1}{2}\)の等比数列です。そのため、以下の式を作れます。
- \(p_{n+1}-p_{n}=\displaystyle\frac{1}{4}·\left(-\displaystyle\frac{1}{2}\right)^{n-1}\) – ①
次に、\(p_n+\displaystyle\frac{1}{2}p_{n-1}=p_{n-1}+\displaystyle\frac{1}{2}p_{n-2}\)に着目しましょう。数列\(\{p_{n+1}+\displaystyle\frac{1}{2}p_{n}\}\)は初項\(p_{2}+\displaystyle\frac{1}{2}p_{1}=1\)、公比1の等比数列です。そのため、以下の式を作れます。
- \(p_{n+1}+\displaystyle\frac{1}{2}p_{n}=1\) – ②
\(①-②\)より、以下のように計算しましょう。
\(-\displaystyle\frac{3}{2}p_{n}=\displaystyle\frac{1}{4}·\left(-\displaystyle\frac{1}{2}\right)^{n-1}-1\)
\(p_{n}=\displaystyle\frac{2}{3}-\displaystyle\frac{1}{6}·\left(-\displaystyle\frac{1}{2}\right)^{n-1}\)
こうして、隣接3項間の漸化式を利用することによって確率を得ることができました。隣接2項間の漸化式に比べて複雑になるものの、漸化式の性質を利用することによって計算できるようになりましょう。
確率漸化式を作れるようにする
漸化式に関わる問題は難しいものの、特に難問になりやすいのが確率漸化式です。そもそも、漸化式を利用しなければいけない確率の問題であることを見抜けなければいけません。
また、漸化式を作るには適切な方法があります。確率漸化式の解き方を知らない場合、漸化式を作るのは難しいです。そこで、\(n\)回目と\(n+1\)回目に着目することによって漸化式を作れるようになりましょう。
なお確率漸化式に関わる問題には、隣接3項間の漸化式を利用するケースもあります。\(n\)回目に対して、\(n+1\)回目と\(n+2\)回目(または\(n-1\)回目と\(n-2\)回目)を考慮する場合では、隣接3項の漸化式を利用します。
確率漸化式は難問が多く、基本となる例題を解けるようになる必要があります。目的の事象がいつ、何回起こるのか指定されていない場合、確率漸化式を利用して答えを得られるようになりましょう。