最大公約数を素早く見つける方法にユークリッドの互除法(ごじょほう)があります。整数の計算をするとき、ユークリッドの互除法が役に立つ場面は多いです。
数字が小さい場合、最大公約数を見つけるのは簡単です。ただ大きい数字では、最大公約数を見つけるのが難しいです。そこでユークリッドの互除法を利用することによって、効率的に最大公約数を見つけるのです。
またユークリッドの互除法を学ぶと、一次不定方程式の整数解を見つけるときに役立ちます。むしろ、ユークリッドの互除法は一次不定方程式で活躍する場面のほうが多いかもしれません。
なぜ私たちがユークリッドの互除法を習うかというと、単純に便利だからです。ここでは素早く最大公約数を見つけるため、どのようにユークリッドの互除法を利用すればいいのか解説していきます。
もくじ
ユークリッドの互除法によって最大公約数を見つける
効率的に最大公約数を見つける方法がユークリッドの互除法です。それでは、どのようにして最大公約数を見つけるのでしょうか。数式を並べても理解するのは難しいため、実際の数字を利用して最大公約数を見つけてみましょう。
例えば370と259の最大公約数は何でしょうか。ユークリッドの互除法を利用しない場合、ほとんどの人で1分以内に最大公約数を見つけることができません。一方、ユークリッドの互除法を利用する場合、すぐに最大公約数を見つけることができます。
ユークリッドの互除法では、大きい数字を左に置き、小さい数字を右に置きます。その後、割り算の答えと余りを利用して、以下のように計算していきます。

このとき、余りが0になる場面が必ず訪れます。余りが0になるとき、割る数が最大公約数です。公約数で割る場合、当然ながら余りは出ません。そのため、ユークリッドの互除法で余りが0になる場面が最大公約数なのです。
ユークリッドの互除法を文章で読んでも100%の確率で理解できません。そこで、上図の配置を覚えましょう。そうすれば、ユークリッドの互除法の利用手順を覚えることができます。
なぜユークリッドの互除法が利用されるのか
それでは、なぜユークリッドの互除法が利用されるのでしょうか。この理由として、大きい数であっても最大公約数をすぐに見つけることができるからです。
例えば、12と20の最大公約数を見つけるのは簡単です。12と20について、それぞれ約数を出した後、共通する約数の中で最も大きい数字を選べばいいです。
一方、先ほどの例のように、370と259の最大公約数ではどうでしょうか。370と259に共通する約数は37だけです。1から順に数字を当てはめて約数を探してもいいですが、非常に多くの時間がかかります。
そこでユークリッドの互除法を利用しましょう。ユークリッドの互除法を使えば、大きい数であっても素早く最大公約数を発見できます。
一次不定方程式でユークリッドの互除法を利用する
なおユークリッドの互除法を利用して最大公約数を見つけることはできるものの、ユークリッドの互除法が最も利用されるのは一次不定方程式です。
一次方程式の場合、解の数は一つです。一方で一次不定方程式の場合、解は一つではありません。多くの解をもつのが一次不定方程式です。一次不定方程式は以下の数式によって表されます。
- \(ax+by=c\)
例えば、以下の式を満たす\(x\)と\(y\)を解く場合は一次不定方程式です。
- \(9x+5y=1\)
この式の答えは\(x=5k-1\)であり、\(y=-9k+2\)です(\(k\)は整数)。つまり\(k\)に任意の整数を代入することによって、答えをいくつも作ることができます。このように特定の値ではなく、数式を利用することによって整数解を出すのが一次不定方程式です。
互いに素の場合、整数解が存在する
なおユークリッドの互除法を利用して一次不定方程式の整数解を見つけるとき、私たちが事前に理解するべき内容が以下です。
- \(a\)と\(b\)が互いに素のとき、任意の整数\(c\)について、\(ax+by=c\)を満たす整数\(x\)と整数\(y\)が存在する。
つまり\(ax+by=c\)について整数解を得るためには、\(a\)と\(b\)が互いに素である必要があります。そのため一次不定方程式を利用する場合、必ず互いに素の関係を活用しましょう。
・一次不定方程式の整数解を見つける
それでは、どのように一次不定方程式の整数解を見つければいいのでしょうか。最もわかりやすい方法としては、ユークリッドの互除法を利用せず、自力で答えを発見する方法です。例えば、以下の一次不定方程式の整数解は何でしょうか。
- \(3x+2y=7\) … ①
一次不定方程式の整数解を得るためには、ランダムに代入することで答えを一つ見つけましょう。例えば\(x=1,y=2\)の場合、式を満たします。そこで、以下のように代入しましょう。
- \(3×1+2×2=7\) … ②
次に、①から②を引きましょう。
\(3(x-1)+2(y-2)=0\)
\(3(x-1)=-2(y-2)\)
3と2は互いに素です。そのため、\(x-1\)は2の倍数であるとわかります。そこで、\(x-1\)を以下のように表しましょう。
\(x-1=2k\)(\(k\)は整数)
そこで、\(x-1=2k\)を代入しましょう。
\(3(x-1)=-2(y-2)\)
\(3×2k=-2(y-2)\)
\(-3k=y-2\)
\(y=-3k+2\)
また前述の通り、\(x-1=2k\)です。そのため以下のようになります。
\(x-1=2k\)
\(x=2k+1\)
こうして、\(x=2k+1\)と\(y=-3k+2\)が答えであるとわかりました(\(k\)は整数)。
互除法を利用し、一組の解を見つける方法
ただ、一次不定方程式の整数解を得るとき、一組の解を見つけるのが難しいケースがあります。その場合、ユークリッドの互除法を利用して一組の解を見つけましょう。例えば、以下の一次不定方程式の整数解は何でしょうか。
- \(29x-12y=2\)
この式について、ユークリッドの互除法を利用して問題を解きましょう。
なお先ほど説明した方法とは異なり、最大公約数ではなく、一次不定方程式の整数解を得るためにユークリッドの互除法を利用します。このとき、ユークリッドの互除法による計算では、余りが0ではなく、1になることを理解しましょう。
ただ、余りが1になること以外は計算方法が同じです。先ほどの式であれば、29と12を利用してユークリッドの互除法を活用しましょう。大きい数字である29を左に置き、12を右に置き、以下のように計算します。
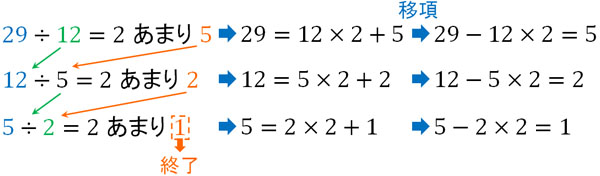
このときは割り算をかけ算で表し、移項することで上図の式を作りましょう。
次に、ユークリッドの互除法を利用して作った式について、上の式を下の式へ順に代入していきましょう。以下のようになります。
・\(12-5×2=2\)を\(5-2×2=1\)へ代入
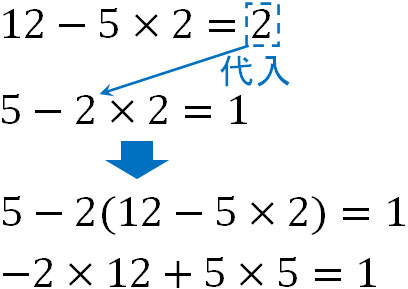
次に、ユークリッドの互除法で得た一番上の式を先ほどの式に代入しましょう。
・\(29-12×2=5\)を\(-2×12+5×5=1\)へ代入
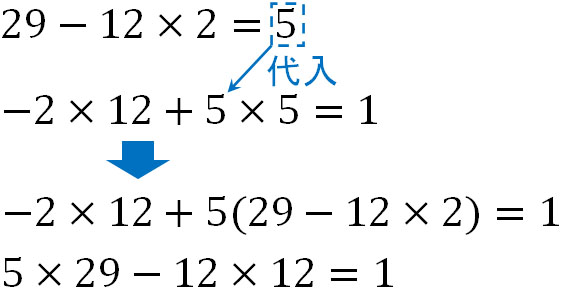
こうして、\(5×29-12×12=1\)を得ることができました。
ユークリッドの互除法を利用する場合、最初の式で\(a\)と\(b\)(今回の例題では29と12)を必ず使います。そのため\(a\)と\(b\)が互いに素の場合、ユークリッドの互除法によって\(a\)と\(b\)を利用した整数解を必ず得ることができます。
また今回の計算では、ユークリッドの互除法を利用して代入後、式を整理するとき、29と12を式の中に残しています。この理由として、後で引き算をするときに必要になるからです。
・一組の整数解を得る
それでは次に\(5×29-12×12=1\)を利用して、\(29x-12y=2\)の整数解を得ましょう。その前に、引き算をすることによって右辺を0にする必要があるため、\(5×29-12×12=1\)を2倍にしましょう。
\(5×29-12×12=1\)
\(10×29-24×12=2\)
これはつまり、\(29x-12y=2\)の整数解の一つが\(x=10\)、\(y=24\)であることを意味しています。次に、\(29x-12y=2\)から\(10×29-24×12=2\)を引きます。
\(29(x-10)-12(y-24)=0\)
\(29(x-10)=12(y-24)\)
29と12は互いに素であるため、\(x-10\)は12の倍数です。そのため、以下のように表すことができます。
\(x-10=12k\)
\(x=12k+10\)(\(k\)は正の整数)
次に、\(x-10=12k\)を\(29(x-10)=12(y-24)\)に代入しましょう。
\(29(x-10)=12(y-24)\)
\(29×12k=12(y-24)\)
\(29k=y-24\)
\(y=29k+24\)(\(k\)は正の整数)
こうして、\(x=12k+10\)と\(y=29k+24\)が答えであるとわかりました(\(k\)は正の整数)。複雑な一次不定方程式であっても、ユークリッドの互除法を使えば答えを出すことができます。
最大公約数を見つけるときよりも、一次不定方程式の整数解を見つけるときにユークリッドの互除法が利用されます。そこで、ユークリッドの互除法を用いて問題を解く手順を覚えましょう。
ユークリッドの互除法を利用して整数解を得る
数字が大きい場合、最大公約数を見つけるのが難しいです。そこで最大公約数を効率的に見つける方法として、ユークリッドの互除法が利用されます。
なおユークリッドの互除法というのは、最大公約数を見つけるときのツールというよりも、一次不定方程式の整数解を見つけるときにひんぱんに利用されます。一次不定方程式で一組の解を得るとき、ユークリッドの互除法を使いましょう。
ユークリッドの互除法について、最大公約数を見つけるときと一次不定方程式で整数解を見つけるときでは、手順が異なります。そこで、それぞれの計算方法を覚えるようにしましょう。
最大公約数の発見や一次不定方程式の問題を解くとき、ユークリッドの互除法を利用することで答えを出せるようになると効率的です。