高校数学で学ぶ内容としてチュバの定理とメラニウスの定理があります。公式は複雑であり、公式を覚えても利用することはできません。
そこで、チュバの定理とメラニウスの定理は覚えないようにしましょう。公式を覚えるのではなく、公式を作れるようにするのです。そうすればすべての図形問題について、チュバの定理とメラニウスの定理を利用して計算することができます。
なおチュバの定理やメラニウスの定理を利用すれば、辺の比や面積を計算できるようになります。そこで、これらの定理を利用して問題を解けるようになりましょう。
チュバの定理やメラニウスの定理は一見すると複雑です。ただ覚え方を理解すれば、公式を暗記しなくても定理を利用できるようになります。そこで、どのようにチュバの定理やメラニウスの定理を利用すればいいのか解説していきます。
もくじ
三角形の辺の比を利用するチュバの定理とメラニウスの定理
三角形の辺の比を利用する定理にチュバの定理とメラニウスの定理があります。
チュバの定理では、△ABCの内部に任意の点Oを取ります。このときAO、BO、COの延長線との交点をそれぞれP、Q、Rとします。その場合、以下の関係が成り立ちます。
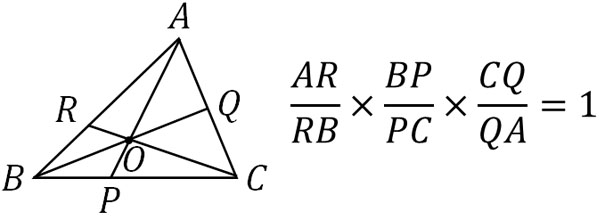
これがチュバの定理です。それぞれの辺について、比とかけ算を利用することで答えが1になるのです。
また、メラニウスの定理はチュバの定理と基本的に内容が同じです。先ほど、三角形の内部に点Oを取りました。次は、辺の上または辺の延長線上に点Pを取りましょう。その場合、以下の関係が成り立ちます。
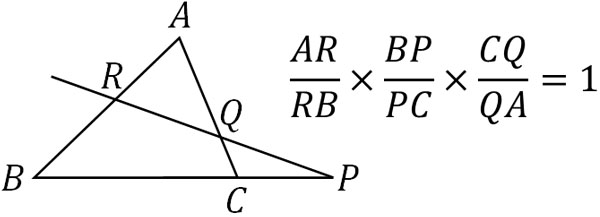
これがメラニウスの定理です。チュバの定理と同様に、辺の比とかけ算を利用することによって1になります。
チュバの定理の覚え方
一見すると、チュバの定理は複雑です。ただ、先ほどの公式は覚えないようにしましょう。公式を覚える場合、必ず忘れてしまいます。そこで、公式を作れるようにしましょう。
チュバの定理を作る方法は簡単です。特定の頂点(例えば点A)を出発し、通った順に「分子→分母→分子→…」と埋めていきます。
最初はAを出発してRに到着します。その後、RからBに行きます。そこで、以下のように記します。
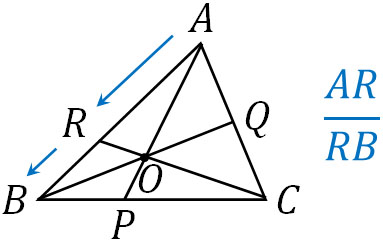
次に、BからPを通り、Cに行きます。そこで先ほど同様にBPを分子に置き、PCを分母に置きます。
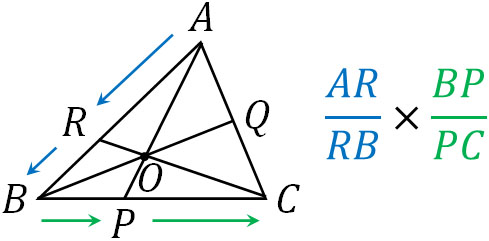
最後に、CからQを通り、Aに戻ります。そこでCQを分子に置き、QAを分母に置きましょう。
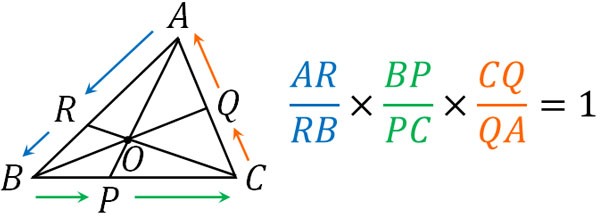
こうして、チュバの定理を作ることができます。作り方を覚えれば、チュバの定理を暗記する必要はまったくないとわかります。一つの頂点から出発し、「分子→分母→分子→…」と順に記していけば公式を作ることができます。
メラニウスの定理の覚え方
チュバの定理を作れるようになったら、次にメラニウスの定理を作れるようになりましょう。作り方は先ほどの説明とまったく同じです。特定の点から出発し、通った点を利用して「分子→分母→分子→…」と順に記していきましょう。
頂点Aからスタートする場合、以下のようにRを通り、Bに行きます。そのためARが分子であり、RBが分母です。
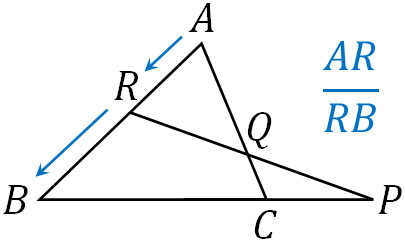
次に、BからPまで移動します。その後、PからCまで戻ります。そこでBPを分子、PCを分母に置きます。
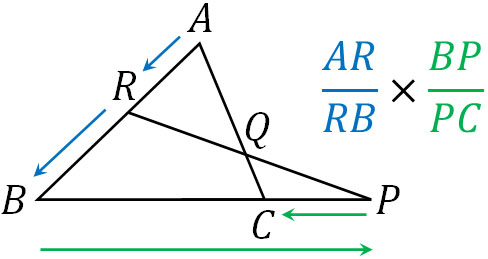
最後に、CからQを通り、Aへ到着します。そこでCQを分子にして、QAを分母にしましょう。
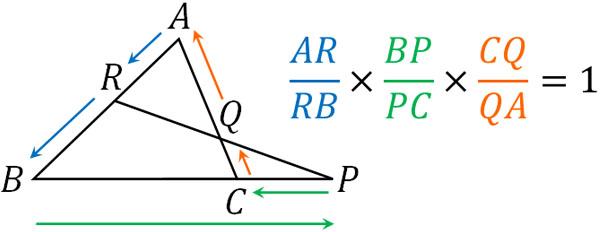
こうして、メラニウスの定理を作ることができます。一見すると公式は複雑であるものの、作り方を覚えればすべての図形問題に対処できるようになります。
なお、チュバの定理に比べるとメラニウスの定理は少し複雑になります。メラニウスの定理というのは、三角形と直線で成り立っています。そのため、三角形と直線の関係を把握してメラニウスの定理を作れるようになりましょう。
辺の比を求める例題
それでは、実際にメラニウスの定理を利用して問題を解いてみましょう。以下の問題の答えは何でしょうか。
- △ABCについてAB、BC、CAを1:2に内分する点をそれぞれL、M、Nとします。また、それぞれの交点が以下の図のようになるとき、AP:PQ:QMの比率を求めましょう。
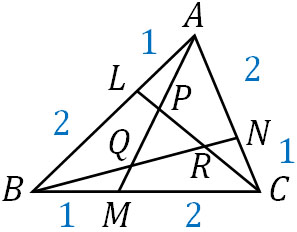
チュバの定理ではなく、メラニウスの定理を利用して問題を解きます。そこで、三角形と直線の関係に着目しましょう。
まず、以下の三角形と直線に着目します。
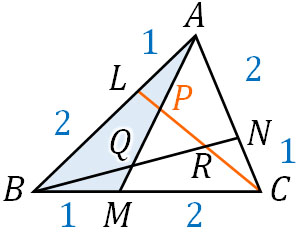
そうすると、以下の式を作ることができます。
\(\displaystyle\frac{1}{2}×\displaystyle\frac{3}{2}×\displaystyle\frac{PM}{AP}=1\)
\(\displaystyle\frac{3}{4}×\displaystyle\frac{PM}{AP}=1\)
\(\displaystyle\frac{PM}{AP}=\displaystyle\frac{4}{3}\)
\(3PM=4AP\)
こうして、PM:AP=4:3であるとわかります。それでは次に、以下の三角形と直線に着目しましょう。
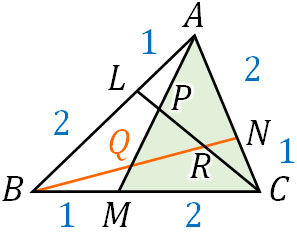
この場合、メラニウスの定理を利用して以下の式を作れます。
\(\displaystyle\frac{2}{1}×\displaystyle\frac{3}{1}×\displaystyle\frac{QM}{AQ}=1\)
\(6×\displaystyle\frac{QM}{AQ}=1\)
\(6QM=AQ\)
こうして、AQ:QM=6:1であるとわかります。
またAQ:QM=6:1であるため、\(QM=\displaystyle\frac{1}{7}AM\)です。またPM:AP=4:3なので、\(PM=\displaystyle\frac{4}{7}AM\)であり、\(AP=\displaystyle\frac{3}{7}AM\)です。つまり、AP:PQ:QM=3:3:1です。こうして、辺の比を求めることができました。
チュバの定理の逆とメラニウスの定理の逆を利用する
なおチュバの定理とメラニウスの定理を学んだら、次にチュバの定理の逆とメラニウスの定理の逆を理解しましょう。
・チュバの定理の逆
チュバの定理では、三角形の内部にある点を通る直線について、以下の関係が成り立つと解説しました。
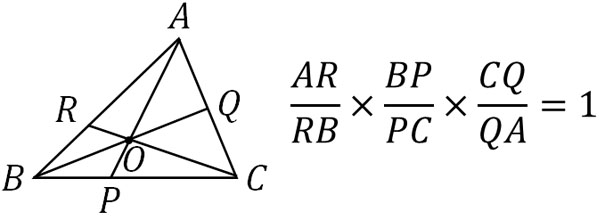
一方、この逆も成り立ちます。つまり、\(\displaystyle\frac{AR}{RB}\)\(×\displaystyle\frac{BP}{PC}\)\(×\displaystyle\frac{CQ}{QA}\)\(=1\)の場合、AP、BQ、CRは一点で交わります。
・メラニウスの定理の逆
また、メラニウスの定理の逆もあります。メラニウスの定理の逆についても、チュバの定理の逆と同じように考えましょう。
前述の通りメラニウスの定理では、三角形と直線について以下の関係が成り立ちます。
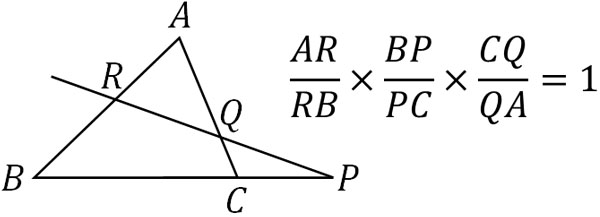
このとき\(\displaystyle\frac{AR}{RB}\)\(×\displaystyle\frac{BP}{PC}\)\(×\displaystyle\frac{CQ}{QA}\)\(=1\)が成り立つのであれば、P、Q、Rは一直線上にあります。これがメラニウスの定理の逆です。
定理を利用して証明問題を解く
それでは、チュバの定理の逆やメラニウスの定理の逆を利用して証明問題を解いてみましょう。チュバの定理やメラニウスの定理だけでなく、チュバの定理の逆とメラニウスの定理の逆も利用できるようにする必要があります。
- △ABCの内部に点Oがあります。∠AOB、∠BOC、∠COAの二等分線と辺との交点をそれぞれL、M、Nとします。このときAM、BN、CLが一点で交わることを証明しましょう。
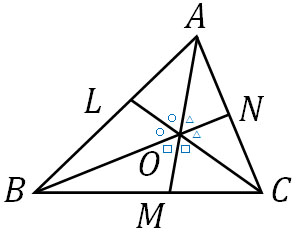
二等分線の定理より、AO:OB=AL:LBです。つまり、以下のようになります。
\(\displaystyle\frac{AL}{LB}=\displaystyle\frac{AO}{OB}\) – ①
同様に二等分線の定理を利用することにより、BO:OC=BM:MCとCO:OA=CN:NAが成り立ちます。そのため、以下のようになります。
\(\displaystyle\frac{BM}{MC}=\displaystyle\frac{BO}{OC}\) – ②
\(\displaystyle\frac{CN}{NA}=\displaystyle\frac{CO}{OA}\) – ③
①、②、③より、以下のようになります。
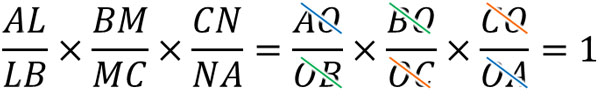
そのためチュバの定理の逆より、AM、BN、CLは一点で交わります。
このようにチュバの定理の逆やメラニウスの定理の逆を利用することによって、証明問題を解くことができます。
チュバの定理とメラニウスの定理を利用できるようにする
ひんぱんに利用される定理ではないものの、知っていないと問題を解けないのがチュバの定理とメラニウスの定理です。
一見すると、チュバの定理やメラニウスの定理は複雑です。ただ公式の作り方を理解していれば、公式を作ることができます。また実際のところ、公式を覚えても図が変わると混乱する人がほとんどです。そこで、公式を作れるようにしましょう。
またチュバの定理やメラニウスの定理では証明問題も出されます。このとき、チュバの定理の逆やメラニウスの定理の逆も利用できるようにしましょう。
公式の作り方を知っているかどうかによって、チュバの定理やメラニウスの定理の難易度が大幅に違います。そこで公式の作り方を覚え、ここまで解説した内容と異なる図を提示されたとしても問題を解けるようになりましょう。