数式で不等式を利用することにより、特定の領域を表すことができます。特定の領域よりも大きい数、または小さい数を記すのです。
それでは連立方程式を利用したり、絶対値を含んだりする場合、不等式が表す領域はどのように考えればいいのでしょうか。このときかけ算を含む場合についても、不等式が表す領域は複雑になります。
また不等式が表す領域について、最大値と最小値を計算できるようになりましょう。特定の領域の中での最大値と最小値というのは、見つけ方が決まっています。頂点や境界線、角、接点などに着目することにより、最大値や最小値を得ることができます。
それでは、どのように考えて不等式が表す領域を図示すればいいのでしょうか。不等式を含む式の解き方を解説していきます。
もくじ
方程式によって異なる不等式の表す領域
それぞれの方程式について、不等式の表す領域を理解しましょう。内容は難しくなく、直線や放物線、円について、不等式の向きと領域の関係を学ぶのです。それぞれ以下のようになります。
・直線
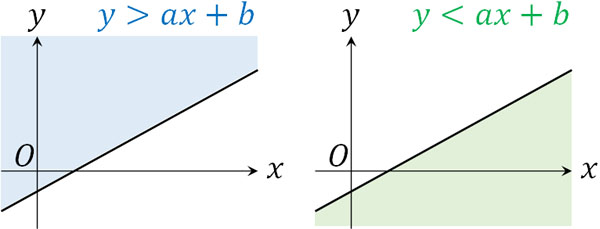
\(y>ac+b\)というのは、直線\(y=ac+b\)よりも\(y\)の値が大きい場所を指します。一方、\(y<ac+b\)ではその反対になります。
・放物線
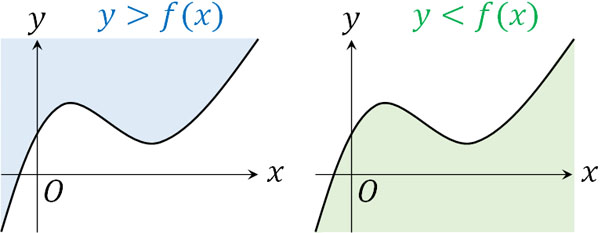
\(y>f(x)\)では、\(f(x)\)よりも\(y\)の値が大きい領域を指します。それに対して\(y<f(x)\)では、\(f(x)\)よりも\(y\)の値が小さい領域を指します。
・円
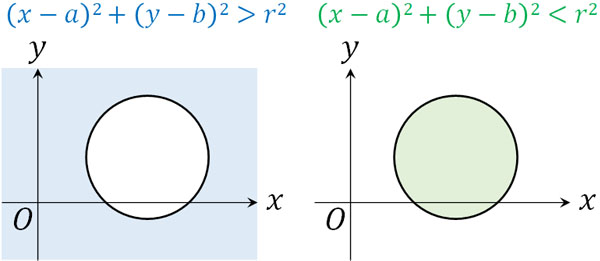
\(r\)は半径を表します。そのため\((x-a)^2+(y-b)^2>r^2\)は半径\(r\)の外側を表します。それに対して、\((x-a)^2+(y-b)^2<r^2\)は半径\(r\)の内側を表します。
それぞれの方程式が何を意味しているのか理解している場合、不等式の向きと領域の場所を関連付けるのは簡単です。
連立方程式による不等式の表す領域
それでは2つの方程式が存在する場合、不等式による領域はどのように考えればいいのでしょうか。連立方程式による不等式の表す領域では、両方の式を満たす領域を答えましょう。それでは以下の領域を図示すると、どのようになるでしょか。
\(\begin{eqnarray} \left\{\begin{array}{l}x^2+y^2<4\\y<x-1\end{array}\right.\end{eqnarray}\)
この式の意味は「\(x^2+y^2<4\)、かつ\(y<x-1\)を満たす領域」を指します。この意味を理解すれば、領域を図示するのは簡単です。まず、以下のようにそれぞれの式について領域を図示しましょう。
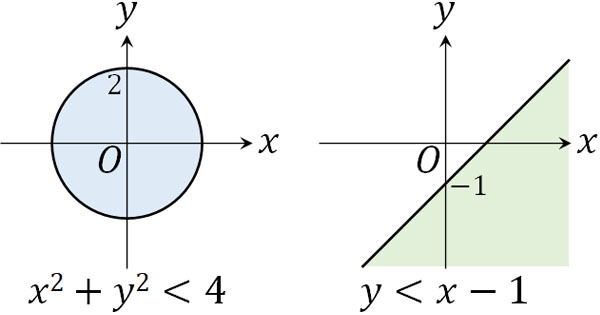
その後、2つの式を満たす領域を図示します。

※境界線は領域に含まない。
こうして、不等式の表す領域を図示することができました。連立方程式が「かつ(&)」を意味することを理解すれば問題を解くことができます。
絶対値を含む場合の不等式の表す領域
次に絶対値を含む場合について、不等式の表す領域を学びましょう。絶対値が存在する場合、絶対値を外すときに場合分けをしなければいけません。絶対値を外すとき、プラスまたはマイナスを加えるようにしましょう。
それでは以下の領域を図示すると、どのようになるでしょうか。
- \(|x+y|<1\)
絶対値を外すとき、絶対値の中がプラスなのか、それともマイナスなのかによって場合分けをします。そこで、以下の2パターンを考えましょう。
- \(x+y<1\)
- \(-(x+y)<1\)
\(-(x+y)<1\)は\(x+y>-1\)です。つまり\(x+y<1\)、かつ\(x+y>-1\)の領域を図示すればいいです。そのため、答えは以下のようになります。
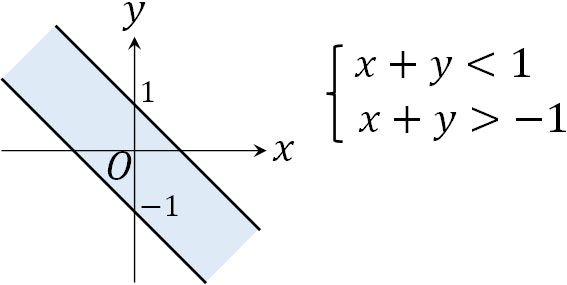
※境界線は領域に含まない。
次に、以下の領域を図示してみましょう。
- \(|x|+|y|<1\)
この場合、絶対値を外すために4つの場合分けが必要になります。以下のようになります。
- \(x>0,y>0\):\(x+y<1\)
- \(x<0,y>0\):\(-x+y<1\)
- \(x>0,y<0\):\(x-y<1\)
- \(x<0,y<0\):\(-x-y<1\)
そこで、すべての条件を満たす領域を図示しましょう。
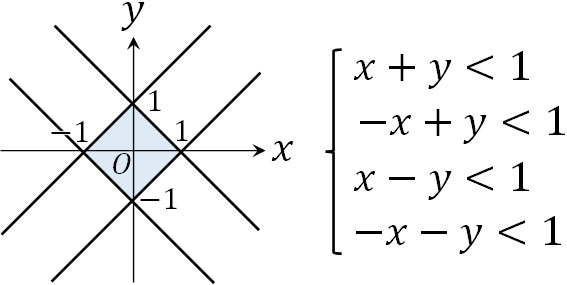
※境界線は領域に含まない。
こうして、領域を図示することができました。いずれにしても、絶対値を外すときはプラスとマイナスで場合分けをすればいいとわかります。
かけ算を含む場合、不等式の表す領域はどうなるのか
それでは、式がかけ算を含む場合はどのように計算すればいいのでしょうか。この場合についても、場合分けをすることで領域を図示しましょう。以下の式について領域を図示すると、どのようになるでしょうか。
- \((x+y-2)(y-x^2)>0\)
この場合、\(x+y-2\)と\(y-x^2\)の両方が0よりも大きい場合、不等式を満たします。または、\(x+y-2\)と\(y-x^2\)の両方が0よりも小さい場合(両方とも値がマイナスの場合)についても不等式を満たします。つまり、以下のケースを考えればいいとわかります。
\(\begin{eqnarray} \left\{\begin{array}{l}y>-x+2\\y>x^2\end{array}\right.\end{eqnarray}\)
または
\(\begin{eqnarray} \left\{\begin{array}{l}y<-x+2\\y<x^2\end{array}\right.\end{eqnarray}\)
そこで2つの連立方程式について、それぞれ領域を図示した後に足しましょう。
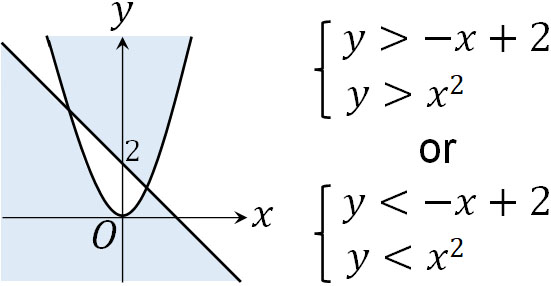
※境界線は領域に含まない。
こうして、図示することができました。かけ算をするとき、符号を確認することで答えを得ましょう。
一次式での領域の最大値と最小値
それでは不等式が表す領域について、最大値と最小値を計算するにはどのようにすればいいのでしょうか。方法としては、領域を図示した後、\(f(x,y)=k\)として最大値と最小値を計算しましょう。
実際に問題を解かないと計算方法を理解できないと思いますので、以下の問題を解きましょう。
- \(y≦x\)、\(x-2y≦1\)、\(2x-y≦2\)をすべて満たす\(x\)と\(y\)について、\(x+4y\)の最大値と最小値を求めましょう。
まず、領域を以下のように図示しましょう。
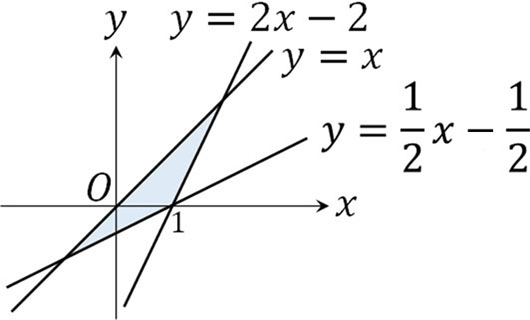
※境界線は領域に含む。
次に\(x+4y=k\)としましょう。この式を変形すると、\(y=-\displaystyle\frac{1}{4}x+\displaystyle\frac{k}{4}\)の直線であり、傾き\(-\displaystyle\frac{1}{4}\)、切片\(\displaystyle\frac{k}{4}\)とわかります。
それでは\(k\)の値が最大になる場所はどこでしょうか。言い換えると、切片\(\displaystyle\frac{k}{4}\)が最大になる場合、図でどの場所を通ればいいでしょうか。図を確認すると、直線\(y=-\displaystyle\frac{1}{4}x+\displaystyle\frac{k}{4}\)が\((2,2)\)を通るとき、\(k\)の値が最大になるとわかります。
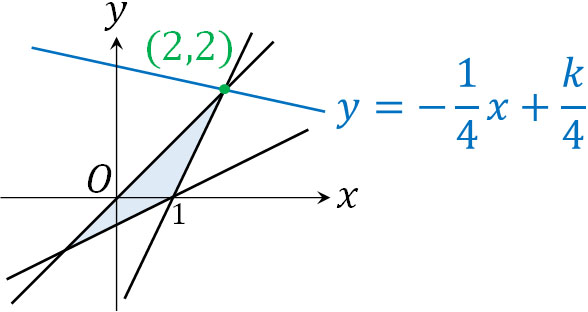
そこで\(x+4y=k\)に\((2,2)\)を代入すると、\(k=10\)とわかります。
それでは、切片\(\displaystyle\frac{k}{4}\)が最小になる場合、図のどの場所を通ればいいでしょうか。図を確認すると、直線\(y=-\displaystyle\frac{1}{4}x+\displaystyle\frac{k}{4}\)が\((-1,-1)\)を通るとき、\(k\)の値が最小になるとわかります。
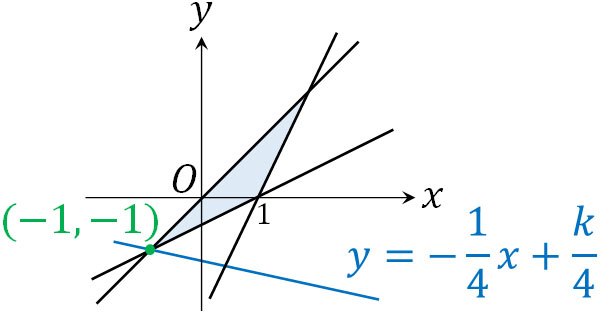
そこで\(x+4y=k\)に\((-1,-1)\)を代入すると、\(k=-5\)とわかります。こうして、最大値\(10\)と最小値\(-5\)を得ることができました。
放物線や円の最大値・最小値では角や接点に着目する
なお放物線や円を含む式について最大値と最小値を計算する場合、角に加えて、接点に着目することによって最大値や最小値を得られるケースがあります。例題として、以下の問題を解きましょう。
- \(x\)と\(y\)が\(x^2+y^2≦4\)、\(x≦0\)を満たすとき、\(-x+y\)の最大値と最小値を求めましょう。
図を描くと領域は以下のようになります。
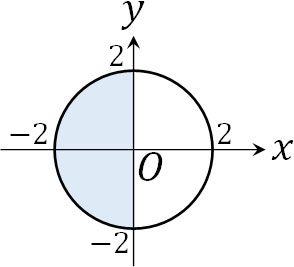
次に\(-x+y=k\)としましょう。つまり、\(y=x+k\)です。最小値を得るのは簡単であり、\(k\)の値が最小となるためには、\((0,-2)\)を通ればいいとわかります。つまり、最小値は\(k=-2\)です。
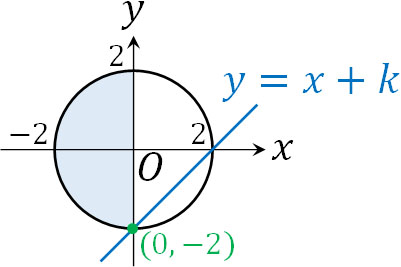
一方で最大値を得るためには、円の接点を通らなければいけません。そこで、直線と円の方程式を連立して計算しましょう。\(y=x+k\)と\(x^2+y^2=4\)を連立させると以下のようになります。
\(x^2+y^2=4\)
\(x^2+(x+k)^2=4\)
\(2x^2+2kx+k^2-4=0\)
直線と円が接するためには、\(2x^2+2kx+k^2-4=0\)が重解をもつ必要があります。そこで、判別式\(D\)が0になる値を計算しましょう。
\((2k)^2-4×2×(k^2-4)=0\)
\(4k^2-8k^2+32=0\)
\(k^2=8\)
\(k=±2\sqrt{2}\)
接線の方程式は2つあります。ただ図より、円の左上で接する円が正解であるとわかります。そのため切片\(k\)の値がプラスである\(k=2\sqrt{2}\)を利用しましょう。
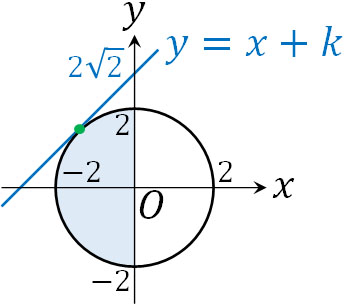
こうして、最大値は\(k=2\sqrt{2}\)になるとわかりました。
図形の通過領域を計算する
次に、図形の通過領域を学びましょう。私たちは数学で\(a\)や\(b\)などの文字を定数として扱い、\(x\)や\(y\)などの文字を変数として扱って計算問題を解きます。それでは、\(a\)や\(b\)などの文字が変数の場合、どのように領域を考えればいいのでしょうか。以下の問題を解いてみましょう。
- 直線\(y=2ax-a^2\)について、\(a\)がすべての実数値で変化するとき、直線が通過する領域を図示しましょう。
まず、具体的な数字を用いて考えましょう。直線は\((1,-3)\)を通過するでしょうか。\(y=2ax-a^2\)は\(a^2-2ax+y=0\)であるため、値を代入して計算すると以下のようになります。
\(a^2-2a-3=0\)
\((a-3)(a+1)=0\)
\(a=-1,3\)
こうして、\(a=-1\)または\(a=3\)のとき、直線は\((1,-3)\)を通過するとわかります。一方、直線は\((1,2)\)を通過するでしょうか。先ほどと同じように計算しましょう。
\(a^2-2a+2=0\)
\(a=1±i\)
こうして、実数解をもたないことがわかります。それでは、一般化して考えてみましょう。直線は\((x,y)\)を通過するでしょうか。
\(a^2-2x·a+y=0\)を\(a\)の二次方程式と捉えましょう。\(a\)が実数解をもつためには、\(a\)を基準に判別式\(D\)を利用すればいいとわかります。そのため、計算は以下のようになります。
\((-2x)^2-4y≧0\)
\(4x^2-4y≧0\)
\(y≦x^2\)
つまり\(y≦x^2\)の場合、\(a\)は実数解をもちます。\(a\)が実数解をもつ場合、直線は\(y≦x^2\)となる領域のどこかを通ることになります。そこで\(y≦x^2\)を図示すると以下のようになります。
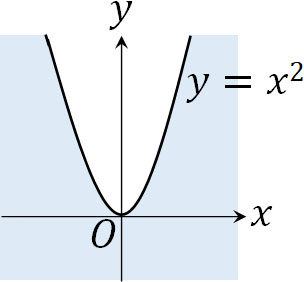
※境界線は領域に含む。
図形の通過領域では\(a\)を変数と考え、\(x\)と\(y\)を定数と考える必要があります。\(x\)と\(y\)を定数とする場合であっても、二次方程式や判別式を利用できるようになりましょう。
不等式が表す領域を図示できるようにする
数式に不等式を含む場合、どの領域を表しているのか理解できるようになりましょう。一つの式に不等式を含む場合、どの領域を表しているのかわかりやすいです。このとき、連立方程式や絶対値、かけ算を含む式についても領域を図示できるようになりましょう。
領域を図示できるようになった後、最大値と最小値を計算できるようになる必要があります。式に対して\(k\)を利用し、図を用いて最大値と最小値を計算しましょう。角や境界線、接点に着目すると、最大値と最小値を得られるようになります。
また領域が関わる数学の問題では、図形の通過領域も出題されます。この場合、\(a\)や\(b\)などの文字を変数とみなして計算しましょう。
不等式が表す領域を図示するとき、問題の解き方があります。そこで、どのように図を利用して答えを得ればいいのか学びましょう。






