ヤングの実験：波の干渉条件と公式の導出方法

光が当たるとき、全体が明るくなるとは限りません。波の干渉により、明るい部分と暗い部分を生じることがあります。

波の干渉では、スクリーンに光を映す場面を学びます。こうした学習内容にヤングの実験があります。ヤングの実験では、光を利用することによって波の干渉が起こり、明暗の線を作ることができるのです。

波の干渉条件を理解していれば、ヤングの実験での波の干渉を学ぶことができます。ヤングの実験で距離の差を計算するとき、複雑な計算過程が必要になります。ただ概念は波の干渉条件と同じであり、利用する公式に変化はありません。

それでは、ヤングの実験での波の干渉はどのように計算すればいいのでしょうか。スクリーンを利用する波の干渉について解説していきます。

ヤングの実験の概要

光の干渉を理解するとき、公式を暗記しても意味がありません。応用問題が出されるとき、問題を解けないからです。そこで、どのように公式を得るのか学びましょう。

スクリーンを用いる波の干渉で重要な内容にヤングの実験があります。ヤングの実験では、スリット（細いすき間）をもつ2つの板を利用します。光をスリットに通すと、回折によって波は広がって進みます。その結果、以下の図のようにスクリーンに明暗の線が作られるのです。

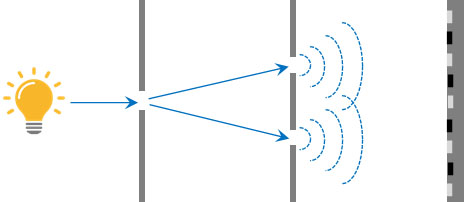
波の干渉を学んでいる場合、スクリーンに明暗の線を生じる現象は問題なく理解できると思います。

なお、最初に単スリット（一つのスリット）を通す理由として、単スリットを利用しないとさまざまな場所から光が侵入してしまい、波の干渉が起こらないからです。つまり、壁全体が明るくなるのです。

窓から入る光が壁に当たるとき、壁に明暗の線は作られません。これは、さまざまな角度の光が入るからです。一方で同じ性質をもつ2つの波が干渉する場合、強め合う場所と弱め合う場所ができます。

強め合う条件と弱め合う条件

それでは、どのようなときに波が強め合ったり、弱め合ったりするのでしょうか。スクリーンに映る光というのは、光源は同じです。そのため当然ながら同位相であり、波の形も同じです。また同位相の波では、以下の式に当てはまる場合は2つの波は互いに強め合います。

• $|AP-BP|=\displaystyle\frac{λ}{2}×2m$ （$m=0,1,2…$）

つまり、光の距離の差が半波長の偶数倍であれば波は強め合います。また波同士が弱め合うとき、以下の式になります。

• $|AP-BP|=\displaystyle\frac{λ}{2}×(2m+1)$ （$m=0,1,2…$）

ここまでは波の干渉条件の知識で理解できます。そこで、ヤングの実験に当てはまるように式を作り変えましょう。ヤングの実験では以下のようになります。

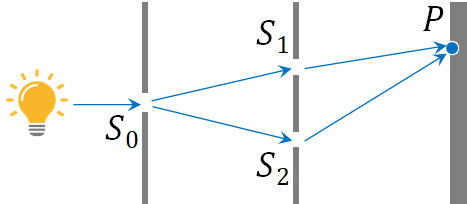
図より、波の干渉が起こるとき、S₁PとS₂Pの距離の差が半波長の偶数倍であれば波は強め合います。またS₁PとS₂Pの距離の差が半波長の奇数倍であれば波は強め合います。そのため、以下の式を作ることができます。

【強め合う場合】

• $|S_1P-S_2P|=\displaystyle\frac{λ}{2}×2m$ （$m=0,1,2…$）

【弱め合う場合】

• $|S_1P-S_2P|=\displaystyle\frac{λ}{2}×(2m+1)$ （$m=0,1,2…$）

このように、波の干渉条件の公式と同じです。そこで$|S_1P-S_2P|$ を計算すれば、ヤングの実験での公式を得ることができます。

ヤングの実験で$|S_1P-S_2P|$を得る

$|S_1P-S_2P|$を得るとき、単スリットを無視して、複スリット（S₁とS₂のあるスリット）とスクリーンに着目しましょう。そこで、以下の図を作ります。

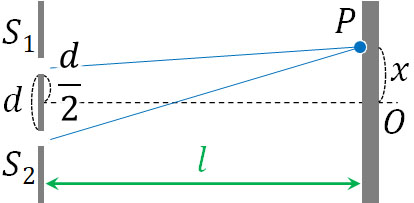
※スリット間の距離$d$は$l$に比べて非常に小さい。

それでは、三平方の定理を用いてS₁PとS₂Pの距離を計算しましょう。以下のようになります。

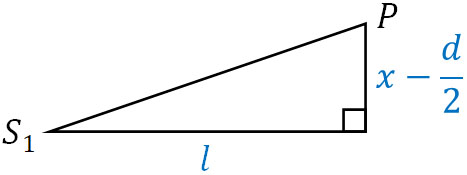
$S_1P=\sqrt{l^2+\left(x-\displaystyle\frac{d}{2}\right)^2}$

$=l\sqrt{1+\left(\displaystyle\frac{x-\displaystyle\frac{d}{2}}{l}\right)^2}$

$=l\left(1+\left(\displaystyle\frac{x-\displaystyle\frac{d}{2}}{l}\right)^2\right)^{\displaystyle\frac{1}{2}}$

なお条件より、スリット間の距離$d$は$l$に比べて値が非常に小さいため、$x-\displaystyle\frac{d}{2}<<l$となります。両辺を$l$で割ると、$\displaystyle\frac{x-\displaystyle\frac{d}{2}}{l}<<1$であることがわかります。

ここで、$|a|<<1$のとき（$|a|$が1に対して非常に小さいとき）、以下が成り立つと知られています。

• $(1+a)^n≒1+na$

物理の問題を解く場合、この式は問題文に提示されます。ただ、この近似式をどのように利用するのか学んでいないと問題を解くことはできないため、ここまで解説した式の変形を理解しなければいけません。

それでは$(1+a)^n≒1+na$を利用し、以下のように近似を用いて計算を進めましょう。

$S_1P=l\left(1+\left(\displaystyle\frac{x-\displaystyle\frac{d}{2}}{l}\right)^2\right)^{\displaystyle\frac{1}{2}}$

$≒l\left(1+\displaystyle\frac{1}{2}\left(\displaystyle\frac{x-\displaystyle\frac{d}{2}}{l}\right)^2\right)$

$=l+\displaystyle\frac{x^2}{2l}-\displaystyle\frac{dx}{2l}+\displaystyle\frac{d^2}{8l}$

こうして、S₁Pの長さを計算することができました。同様にS₂Pの長さを計算すると、以下のようになります。

$S_2P=l+\displaystyle\frac{x^2}{2l}+\displaystyle\frac{dx}{2l}+\displaystyle\frac{d^2}{8l}$

そこで、$|S_1P-S_2P|$を計算しましょう。

$|S_1P-S_2P|$$=l+\displaystyle\frac{x^2}{2l}-\displaystyle\frac{dx}{2l}+\displaystyle\frac{d^2}{8l}$$-\left(l+\displaystyle\frac{x^2}{2l}+\displaystyle\frac{dx}{2l}+\displaystyle\frac{d^2}{8l}\right)$

$=\displaystyle\frac{dx}{l}$

こうして、2つのスリットから発せられる光の距離の差を計算することができました。計算結果より、以下の式を作ることができます。

【強め合う場合】

• $\displaystyle\frac{dx}{l}=\displaystyle\frac{λ}{2}×2m$ （$m=0,1,2…$）

【弱め合う場合】

• $\displaystyle\frac{dx}{l}=\displaystyle\frac{λ}{2}×(2m+1)$ （$m=0,1,2…$）

こうして、2つの波が強め合う場合と弱め合う場合の条件を計算することができました。

ヤングの実験に関する問題を解く場合、必ず計算方法の過程を理解しておく必要があります。計算は複雑であり、計算の途中で近似を利用することになるため、計算方法を学んでいないと問題を解くことができません。

明るい線（または暗い線）の間隔を計算する

それでは、明線の間隔$Δx$はいくらなのでしょうか。同位相の光であるため、S₁とS₂の中点に該当するスクリーン部分（$m=0$）は明るい線になります。つまり、2つの波によって強め合うことになります。

そこで強め合う場合（明るい線を生じる場合）について、以下のように式を変形しましょう。

$\displaystyle\frac{dx}{l}=\displaystyle\frac{λ}{2}×2m$

$\displaystyle\frac{dx}{l}=λm$

$x=\displaystyle\frac{lλ}{d}m$

そこで以下の式に$m=0,1,2…$を代入しましょう。

• $m=0$のとき：$x=0$
• $m=1$のとき：$x=\displaystyle\frac{lλ}{d}$
• $m=2$のとき：$x=\displaystyle\frac{2lλ}{d}$

こうして、明線の間隔$Δx$は$\displaystyle\frac{lλ}{d}$とわかります。

図を利用して明るい線の間隔を求めることはできるものの、計算によって答えを得る場合、$m+1$から$m$を引けばいいです。そこで、以下の計算をします。

$Δx=\displaystyle\frac{lλ}{d}(m+1)-\displaystyle\frac{lλ}{d}m$

$Δx=\displaystyle\frac{lλ}{d}$

こうして、計算によっても明線の間隔$Δx$ は$\displaystyle\frac{lλ}{d}$ とわかりました。また、明るい線の間隔が$\displaystyle\frac{lλ}{d}$ であるため、明線と暗線の間隔は$\displaystyle\frac{lλ}{2d}$ になります。

なお問題の設定が変われば、明線と暗線が出現する条件も変化します。そのため、公式を暗記しても問題を解くことはできません。そこで、距離の差を計算することで干渉条件の式を出しましょう。そうすれば、すべてのケースで答えを得ることができます。

sinθとtanθでの近似を利用する計算方法

なお先ほど、経路差を計算するときに三平方の定理を利用しました。距離の差を出すとき、角度を利用して計算する方法もあります。そこで、sinθとtanθを利用することでヤングの実験での式を得る方法も学びましょう。

条件より、スリット間の距離$d$は$l$に比べて値が非常に小さいです。そのため、S₁PとS₂Pを平行とみなすことができます。

上図のように実際には平行ではないものの、平行とみなすことで近似するのです。また下図を作ると、S₂HがS₁PとS₂Pの距離の差であるとわかります。

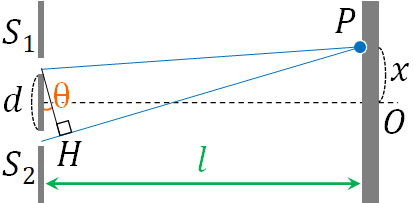
そこで、S₂Hの距離を出しましょう。以下のようになります。

• $S_2H=dsinθ$

なおスリット間の距離$d$は$l$に比べて値が非常に小さいため、S₁PとS₂Pを平行とみなせると解説しました。つまり、θの値はほぼ0°です。θの値が非常に小さい場合、$sinθ≒tanθ$が成り立ちます。そこで、近似を利用してsinθをtanθに変えましょう。

• $S_2H=dtanθ$

なお下図より、$tanθ=\displaystyle\frac{x}{l}$です。そのため、距離の差は$\displaystyle\frac{dx}{l}$です。

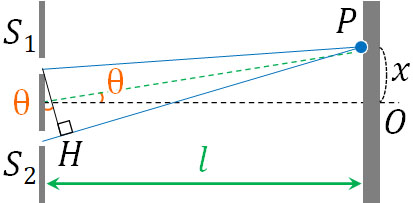
こうして、先ほどの計算と同じ答えを得ることができました。

なお実際には、図に記載している2つのθは角度が異なります。ただ前述の通り、スリット間の距離$d$は$l$に比べて非常に短いため、スリットからスクリーンへ伸びる光は平行であると考えます。その場合、近似によって図にある2つのθを同じ角度と捉えることができます。

ヤングの実験での練習問題

それでは、ヤングの実験に関する練習問題を解いてみましょう。以下の問題の答えは何でしょうか。

• 下図のように、ヤングの干渉実験をします。複スリットS₁とS₂の間隔は$d$であり、複スリットとスクリーンの間隔は$l$です。また、光源の位置を原点Oとし、スクリーン上の点Pの位置を$x$とします。

1. 複スリットの間隔$d$を短くすると、明線の間隔$Δx$はどのように変化しますか。
2. 光源を白色光に変えると、スクリーン上にはさまざまな色が写ります。次数$m$が同じとき、点Oに近い場所では、何色が観察されるでしょうか。

これまでの説明により、波が強め合う場合、以下の式が成り立ちます。

• $\displaystyle\frac{dx}{l}=\displaystyle\frac{λ}{2}×2m$ （$m=0,1,2…$）

そのため、計算によって既にこの式を得ているという前提で先ほどの練習問題を解いていきます。

1) 複スリットの間隔$d$を短くすると、明線の間隔$Δx$はどのように変化しますか

波が強め合うときの間隔（明線の間隔）は先ほど計算した通り以下のようになります。

• $Δx=\displaystyle\frac{lλ}{d}$

そのため複スリットの間隔$d$を短くすると、分母の値は小さくなるため、明線の間隔$Δx$は大きくなるとわかります。

2) 光源を白色光に変えると、スクリーン上にはさまざまな色が写ります。次数$m$が同じとき、点Oに近い場所では、何色が観察されるでしょうか

先ほど計算した通り、$x$は以下の式によって得ることができます。

• $x=\displaystyle\frac{lλ}{d}m$（$m=0,1,2…$）

点Oに近い場合、$x$の値は小さくなります。また$d$と$l$は定数であり、値に変化はありません。同様に問題文より、同じ次数$m$での色の変化を考えます。つまり、変化するのは$λ$のみです。

そのため同じ次数$m$で比べると、原点Oの近くに表れる色というのは、$x$の値が小さくなればいいです。また$x$の値が小さくなるためには、$λ$の値が小さくなればいいとわかります。可視光の中で波長が短いのは紫色や青色です。そのため、正解は紫色や青色です。

ヤングの実験で計算問題を解けるようにする

解き方を知っていない場合、確実に問題を解けないのがヤングの実験に関する問題です。つまり、光の距離の差を計算する方法を知っておく必要があります。

ヤングの実験で距離の差を計算するためには、近似を利用しなければいけません。問題文に近似の式が提示されていても、どこで利用するのか知っていないと適切に近似できません。公式を覚えても意味がないため、必ず計算方法を理解しましょう。

なおヤングの実験では、明線の間隔を計算したり、角度を利用して経路差を得たりしなければいけないケースもあります。そこで、応用問題を含めて問題を解けるようになりましょう。

波の干渉条件の応用がヤングの実験です。計算過程は難しいものの、解き方を知っていれば答えを得ることができます。そこで近似を利用し、距離の差を計算しましょう。