中学数学で出される問題として証明があります。三角形について、図形が等しいことを証明するのです。このとき、平行四辺形が証明問題で出されることが頻繁にあります。
ただ、図形が平行四辺形であることを証明する問題はほぼ出されません。一方で、「平行四辺形の性質を利用して、それぞれの三角形が合同であることを証明する問題」は頻繁に出題されます。
こうした証明問題では、平行四辺形の性質を理解していなければ解くことができません。それでは、平行四辺形の定義は何なのでしょうか。また、平行四辺形の定義から導き出される定理(性質)には何があるのでしょうか。
平行四辺形の性質について学んだあと、どのように証明問題を解けばいいのか解説していきます。
もくじ
平行四辺形の定義と4つの性質
まず、平行四辺形とはどのような図形なのでしょうか。平行四辺形の定義は以下になります。
- 2組の対辺がそれぞれ平行の四角形
平行四辺形では、四角形の向かい合う辺を対辺といいます。また、四角形で向かい合う角を対角といいます。対辺と対角は以下のようになります。

平行四辺形では、対辺がそれぞれ平行です。その場合、以下の性質があります。
- 2組の対辺の長さが等しい
- 2組の対角がそれぞれ等しい
- 隣り合う角度を足すと180°になる
- 2本の対角線はそれぞれの中点で交わる
それぞれの性質について確認していきましょう。
2組の対辺の長さが等しい
2組の対辺がそれぞれ平行な場合、必ず対辺の長さは同じになります。以下のように、それぞれの辺の長さは同じになると理解しましょう。

平行四辺形の図形が問題で出されている場合、「対辺の長さがそれぞれ等しい」という性質を利用して問題を解くようにしましょう。例えば平行四辺形で1つの辺の長さが10cmの場合、対辺の長さは10cmになります。
2組の対角がそれぞれ等しい
平行四辺形では対角が同じです。この性質を利用して角度の計算をしたり、三角形の合同証明(または相似の証明)をしたりすることが頻繁にあります。

向かい合う角度が必ず等しくなることを覚えましょう。例えば1つの角度が60°の場合、対角は同じく60°です。
対辺と対角が等しい証明
それでは、本当に平行四辺形では対辺と対角が等しくなるのでしょうか。この証明をしてみましょう。証明をするためには、以下のように対角線を引きます。
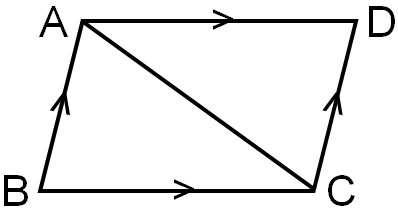
平行四辺形の定義より、AB//DCかつAD//BCです。このとき、△ABCと△CDAを考えましょう。以下のようになります。
- △ABCと△CDAにおいて
- AC=CA:共通の線 – ①
- ∠BAC=∠DCA:平行な線の錯角は等しい – ②
- ∠ACB=∠CAD:平行な線の錯角は等しい – ③
- ①、②、③より、1組の辺とその両端の角がそれぞれ等しいため、△ABC≡△CDA
△ABC≡△CDAなので、AB=DCかつAD=BCです。つまり、対辺はそれぞれ等しいことが分かります。
また∠B=∠Dとなり、対角は等しいです。もう一方の対角については、同じように対角線を引いて三角形が合同であることを証明することで、角度が等しいことを証明できます。ここでは省きますが、いずれにしても平行四辺形では対角が必ず等しくなります。
隣り合う角度を足すと180°になる
対角が等しく、線が互いに平行なので、平行四辺形は他にも性質があります。平行四辺形の定理として、隣り合う角度を足すと180°になります。
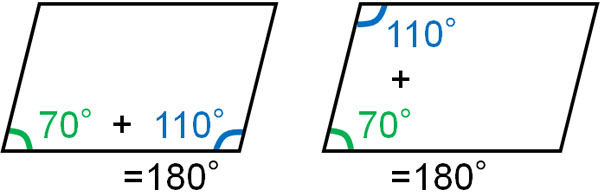
平行四辺形の問題では、この定理を利用して問題を解くことも頻繁にあります。
なぜ、隣り合う角度を足すと180°になるのでしょうか。平行四辺形では、対辺は平行です。平行線の同位角は角度が同じです。そのため、以下のようになります。
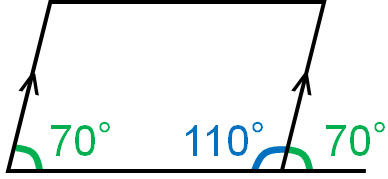
平行四辺形では、一つの角度が分かれば他のすべての角度を計算できます。対角が等しいのは既に説明しました。もう一方の角度については、180°から既知の角度を引くことで計算することができます。
2つの対角線はそれぞれの中点で交わる
平行四辺形には他にも定理があります。平行四辺形では2つの対角線を引くことができ、対角線の交点は中点です。以下のようになります。
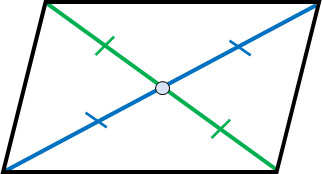
中点なので、同じ長さの線が2つできます。この性質を利用して図形の問題を解かなければいけないこともよくあります。
対角線が中点で交わる証明
なぜ、平行四辺形の対角線の交点は中点になるのでしょうか。同じように、この理由を証明によって説明しましょう。以下の平行四辺形を考えます。
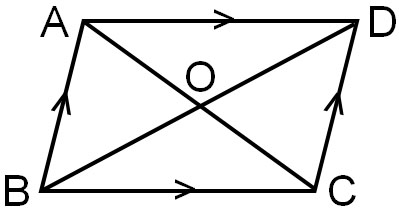
△AOBと△CODについて、合同であることを証明しましょう。そうすれば、対角線の交点が中点になると説明できます。
- △AOBと△CODにおいて
- AB=DC:平行四辺形の対辺は等しい – ①
- ∠BAO=∠DCO:平行な線の錯角は等しい – ②
- ∠ABO=∠CDO:平行な線の錯角は等しい – ③
- ①、②、③より、1組の辺とその両端の角がそれぞれ等しいため、△AOB≡△COD
△AOB≡△CODなので、AO=COかつBO=DOです。そのため平行四辺形では、対角線の交点が中点になることが分かります。
4つの角度がすべて等しいと長方形になる
なお、平行四辺形の中には特殊な形があります。その一つが長方形です。特定の条件を満たす場合、平行四辺形は長方形になります。前述の通り、平行四辺形は対角が等しいです。このとき、すべての角度が等しい場合、長方形になります。
すべての角度が等しくなるためには、角度が90°でなければいけません。辺の長さは違ってもいいですが、角度がすべて同じだと以下のようになります。

長方形は対辺が平行であり、平行四辺形の一種です。ただ、角度がすべて等しい平行四辺形では長方形と呼ばれます。
4つの辺がすべて等しいとひし形になる
他にも特殊な平行四辺形があります。それがひし形です。ひし形の場合、すべての辺の長さが等しくなっています。
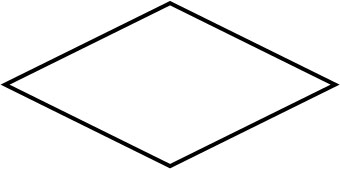
長方形ではすべての角度が等しいです。一方でひし形では、すべての辺の長さが等しいものの、すべての角度が等しくなっている必要はありません。
ひし形の定義は「4つの辺の長さがすべて等しい」です。この定義から導き出される定理として、「対角線が垂直に交わる」があります。以下のようになります。
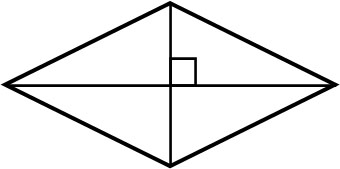
ひし形に対角線を引くことによって、直角三角形を作ることができます。
・正方形は長方形とひし形の性質をもつ
なお、すべての角度と辺の長さが同じである正方形はどうなのでしょうか。この場合、長方形とひし形の両方の性質をもつようになります。もちろん、対角線は垂直に交わります。
練習問題:合同の証明
Q1. 次の図形について証明しましょう
平行四辺形ABCDがあります。対角線の交点をOとし、OE=OFとなるとき、△AOE≡△COFを証明しましょう。
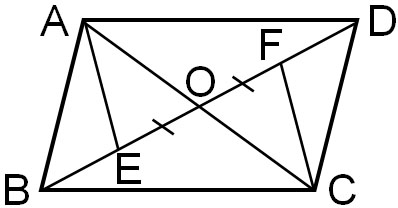
A1. 解答
なぜ、平行四辺形の性質を理解することが重要なのでしょうか。それは、平行四辺形の定義や定理を理解していないと、数学の問題を解くことができないからです。平行四辺形の性質を学ぶことで、問題を解けるようにしましょう。
平行四辺形の定義や定理を利用することで、以下のように証明できます。
- △AOEと△COFにおいて
- OE=OF:仮説より – ①
- ∠AOE=∠COF:対頂角は等しい – ②
- AO=CO:平行四辺形の対角線は中点で交わる – ③
- ①、②、③より、2組の辺とその間の角がそれぞれ等しいため、△AOE≡△COF
平行四辺形を利用した図形の問題では、高確率で平行四辺形の定理を利用して問題を解くことになります。平行四辺形の性質を覚えていなければ解けないため、必ず覚えるようにしましょう。
平行四辺形の性質を利用して証明問題を解く
中学数学で図形の問題を解かなければいけない場合は多いです。このとき、平行四辺形の性質を理解するようにしましょう。
すべての図形の問題に共通しますが、図形がどのような性質を有するのか覚えていない限り、問題を解くことはできません。そのため二等辺三角形や直角三角形など三角形の性質だけでなく、平行四辺形についても学びましょう。
2組の対辺が平行である図形が平行四辺形です。この定義から導き出される性質は主に4つです。これらの定理を利用するからこそ、図形の問題を解くことができます。
特に図形の証明問題で、平行四辺形の性質が頻繁に利用されます。平行四辺形の性質を利用して、三角形の合同や相似の証明をしましょう。






