固体を溶媒(水など)に溶かすとき、最初は溶けるものの、あるときを境に溶けなくなります。溶けなくなった固体は水溶液の中に存在することになります。この状態を溶解平衡といいます。溶解平衡となっている場合、溶媒の中には固体が存在します。
なお通常、どれだけの固体が溶けているのか計算するとき、溶解度曲線を利用します。ただ難溶性の物質では、溶解度曲線を利用しての計算ができません。この場合、溶解度積を利用します。
つまり溶解度積とは、難溶性の物質を計算するときに用いると理解しましょう。また、溶解度積を利用することによって、沈殿を生じるかどうかを判断できます。
それでは難溶性の物質を溶かすとき、どのように溶解度積を利用すればいいのでしょうか。また、沈殿を生じるかどうかを確認するためには、どのように計算すればいいのでしょうか。ここでは、溶解平衡や溶解度積を用いて計算する方法を解説していきます。
もくじ
固体が過剰にあるとき、溶解平衡となっている
塩化ナトリウム(NaCl)を加えると、最初はすべてのNaClが電離して水に溶けます。溶液中にイオンとしてNa+とCl–が存在することになるのです。
ただ過剰の塩化ナトリウムを加えると、水に溶けずに水溶液中に固体で存在することになります。それでは、水に存在する過剰のNaClの表面ではどのような化学反応が起こっているのでしょうか。
見かけ上、水溶液中に存在する固体の塩化ナトリウムの量は同じです。そのため、何も変化していないように思えます。
ただ実際には、塩化ナトリウムの表面を確認すると、NaClは積極的に電離することでイオンになっています。しかし、水溶液中には過剰のNa+とCl–が存在します。そのため、Na+とCl–が結合することによってイオンから固体へと戻る化学反応も起きています。
この状態を表すのが以下の化学反応式です。
- NaCl(固) ⇆ Na+ + Cl–
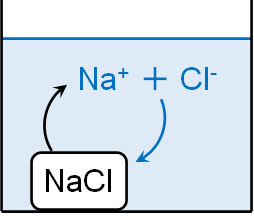
この状態を溶解平衡といいます。溶媒の中に溶けきれていない固体が存在する場合、溶解平衡の状態となっています。
イオンを加えると平衡状態が変わる:共通イオン効果
それでは溶解平衡になっているとき、イオンを加えるとどのような現象が起こるのでしょうか。例えば、飽和食塩水に塩酸(HCl)を加えると、どのようになるでしょうか。
ルシャトリエの原理を学んでいる場合、平衡状態のときにどのような反応が起こるのかわかります。ルシャトリエの原理では、変化を和らげる方向に反応が進行します。
飽和食塩水では、水の中に多くのNa+とCl–が溶けています。この状況で塩酸を加えると、水溶液中に多量のCl–が加わります。そこでルシャトリエの原理より、Cl–の量を減らすように反応が進行します。つまり、平衡は左側に偏ります。
- NaCl(固) ← Na+ + Cl–
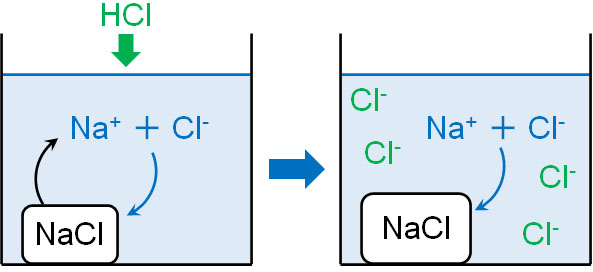
水溶液中に存在するイオンと同じイオンを加えると、平衡状態が変化します。この現象を共通イオン効果といいます。
難溶性の固体(AgClやBaSO4)で重要な溶解度積
ここまで、塩化ナトリウムなど水に溶けやすい物質に着目して解説してきました。それでは、水に対して難溶性の固体はどのように考えればいいのでしょうか。このとき重要になる概念が溶解度積です。
溶解度積について、水に対して溶けにくい塩化銀(AgCl)で確認しましょう。AgClは難溶性の物質であるものの、わずかに水に溶けます。つまりまったく水に溶けないわけではなく、少ないながらも水に溶けることによって平衡状態となっているのです。
このときの溶解平衡は以下のように表すことができます。
- AgCl(固) ⇆ Ag+ + Cl–
それでは、この溶解平衡の平衡定数はどのように表されるのでしょうか。平衡定数Kは以下のようになります。
- \(K=\displaystyle\frac{[Ag^+][Cl^-]}{[AgCl]}\)
ただ前述の通り、水の中に塩化銀(AgCl)を加える場合、AgClはほとんど水に溶けません。そのため、加えた塩化銀のほとんどは水溶液中に固体として存在することになります。これはつまり、AgClのモル濃度はほとんど変化せず、平衡に関与しないことを意味しています。
そこで固体のAgClは一定(定数)とみなし、省きましょう。具体的には、両辺に[AgCl]をかけます。このとき平衡定数Kと[AgCl]の積について、新たな平衡定数としてKspを設定しましょう。
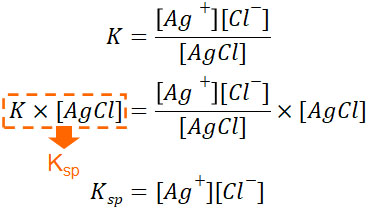
このとき、Kspを溶解度積といいます。温度が一定の場合、溶解度積は常に一定です。
・溶解度積を利用し、固体の溶解度を計算する
それでは、溶解度積に関わる問題を解いてみましょう。以下の問題の答えは何でしょうか。
- AgClの溶解度(mol/L)を求めましょう。なお、AgClの溶解度積は4.0×10-10(mol/L)2とします。
AgClを溶かすとき、1:1の割合でAg+とCl–が生成されます。この積が4.0×10-10になればいいので、[Ag+]と[Cl–]が限界まで溶けているときのモル濃度(溶解度)を\(x\)として、以下の式を作りましょう。
\(x^2=4.0×10^{-10}\)
\(x=2.0×10^{-5}\) \((x>0)\)
溶解度積を利用することによって、AgClの溶解度は2.0×10-5mol/Lとわかりました。
沈殿が生じるかどうかを溶解度積で知る
それでは、溶解度積は何を意味しているのでしょうか。AgClが水に溶けているとき、Ag+またはCl–の量が多くなると、当然ながら固体として析出します。
前述の通り、難溶性の物質は溶解度積を利用して溶解度を計算します。つまり溶解度積よりもモル濃度の積が大きい(水溶液に存在する物質の量が多い)という場合、沈殿を生じることで固体が析出します。
例えば塩化銀の場合、以下のように判断します。
- \(K_{sp}<[Ag^+][Cl^-]\):沈殿を生じる
- \(K_{sp}>[Ag^+][Cl^-]\):沈殿を生じない
等号の向きを覚えるのは意味がありません。そうではなく、なぜこのような関係になるのか理由を理解しましょう。
[Ag+]と[Cl–]のモル濃度が大きくなると、[Ag+][Cl–]の値は大きくなります。当然、[Ag+]と[Cl–]の値が大きいと固体として析出します。このラインがKspであるため、Kspよりも[Ag+]と[Cl–]の積が大きい場合、沈殿を生じます。また、その反対では沈殿を生じません。
溶解度積というのは、難溶性の物質について、沈殿を生じるかどうかを確認するツールでもあります。
なお水へ溶けやすい物質の場合、溶解度曲線を利用することで、結晶として析出するかどうかを判断します。ただ難溶性の物質では、水に溶ける量が非常に少ないです。そこで溶解度曲線ではなく、溶解度積を利用して計算するのです。
溶解度積に関わる沈殿の例題
それでは、沈殿を生じるかどうかについて、どのように判断すればいいのでしょうか。方法は単純であり、イオンのモル濃度を計算しましょう。その後、溶解度積よりも値(モル濃度の積)が大きいのか、それとも小さいのかを確認して判断します。
例えば、以下の問題の答えは何でしょうか。
- Ag+のモル濃度が3.0×10-4mol/Lであり、Cl–のモル濃度が5.0×10-5mol/Lのとき、沈殿を生じるでしょうか。なお、AgClの溶解度積は2.0×10-8(mol/L)2です。
塩化銀について、\(K_{sp}=[Ag^+][Cl^-]\)です。そのため沈殿を生じるかどうか確認するとき、[Ag+]と[Cl–]をかけましょう。
\(3.0×10^{-4}×5.0×10^{-5}=1.5×10^{-8}\)
そこでKsp(2.0×10-8)と[Ag+][Cl–](1.5×10-8)を比較すると、Kspのほうが値は大きいです。これはつまり、Ag+やCl–が水溶液に溶ける余力がまだあることを意味しています。そのため、沈殿は生じません。
沈殿を増やす、または減らす方法
ここまでの内容を理解したら、沈殿を増やす方法(または減らす方法)を学びましょう。難溶性の物質では溶解度積を利用することで沈殿を生じるかどうかを判断するため、沈殿を増やすためには、溶けているイオンと同じイオンを追加すればいいとわかります。
AgClの溶解平衡を再び掲載すると、以下のようになります。
- AgCl(固) ⇆ Ag+ + Cl–
つまりAg+またはCl–の量が増えると、AgClが析出します。そのため、例えばHClを加えると平衡は左側に傾き、AgClが固体として沈殿します。
一方でAg+またはCl–の量が減ると、AgClはイオンになりやすくなります。例えばアンモニアを加えると、以下の反応が起こります。
- Ag+ + 2NH3 ⇆ [Ag(NH3)2]+
こうして、Ag+の量が減ることでAgClがイオンになるように平衡が傾きます。
難溶性の物質について、溶解度積は沈殿の量を増やす(または減らす)ときについても有効なツールです。この性質を利用することによって、沈殿の量を調節できるようになります。
溶解度積を利用し、イオンの状態や沈殿の有無を確認する
水溶液中に溶ける物質であっても、多量に存在すると固体として存在することになります。このときは溶解平衡の状態になっていることを理解しましょう。なお同じ種類のイオンを加えると、溶解平衡が固体生成に傾きます。これが共通イオン効果です。
なお溶解平衡を学ぶとき、難溶性の物質は溶解度積を利用して計算しましょう。難溶性の物質では溶解度曲線を利用できないため、溶解度積を用いるのです。
また溶解度積を利用すれば、液体の中で溶けているのか、それとも沈殿を生じるのか判断できます。それぞれのイオンのモル濃度を計算し、溶解度積を用いて沈殿が起こるかどうか確認しましょう。
イオンになる物質が水溶液中に固体で存在する場合、溶解平衡となっています。そこで、どのように計算問題を解けばいいのか理解しましょう。






