数学では回転体という問題が出題されることがあります。平面の図形について、一回転させた後の図形の体積や表面積を計算するのです。
このような回転体の計算問題はどのように解けばいいのでしょうか。複雑な回転体の図形については、高校数学の積分を学ばなければ計算できません。一方で三角形や四角形など、単純な図形の回転体であれば、中学数学の知識であっても問題を解くことができます。
ただ回転体の問題を解くとき、回転体の図形がどのような形になるのか理解しなければいけません。また、さまざまな図形を組み合わせた応用問題も出されます。そのため回転体では、問題の難易度は高いです。
そこで中学数学での回転体について、どのよう問題を解けばいいのか解説していきます。
もくじ
軸を一回転してできる図形が回転体
空間図形の問題では、角柱や円柱、角錐、円錐、球などの図形が出題されます。ただ、平面の図形であるにも関わらず、空間図形として考えなければいけない問題があります。それが回転体です。
回転体では以下のように、軸を一回転させることで完成する図形を指します。
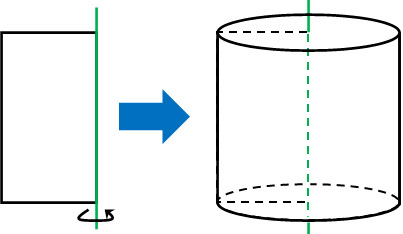
これが回転体です。平面図形から空間図形を作らなければいけません。どのような図形が完成されるのか、あなたの頭の中で想像しなければいけないのです。
その後、回転体の体積や表面積を計算します。例えば、以下の回転体の体積と表面積はどのようになるでしょうか。
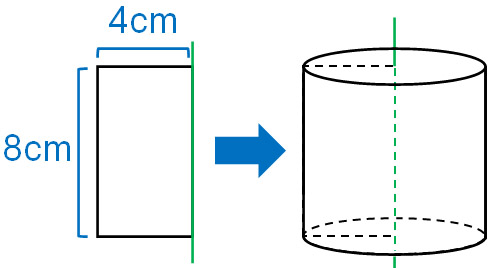
円柱の体積は底面積と高さを掛けることで計算できます。そのため、この回転体の体積は\(128π\)cm3になります。
- \(4×4×π×8=128π\)
一方で表面積は、底面積と側面積を足すことで計算できます。底面積の合計は以下になります。
- \(4×4×π×2=32π\)
また、円柱の側面積は以下になります。
- \(8×π×8=64π\)
そのため、回転体の表面積は\(32π+64π=96π\)となり、答えは\(96π\)cm2です。このように直線で平面図形を一回転させた後、体積と表面積を計算します。
回転体の底面は必ず円になる
このとき回転体には共通点があります。それは、必ず円形になることです。つまり、角柱や角錐の空間図形になることはありません。回転体では必ずカーブのある図形が完成されます。
例として、以下に三角形や半円の回転体を記します。
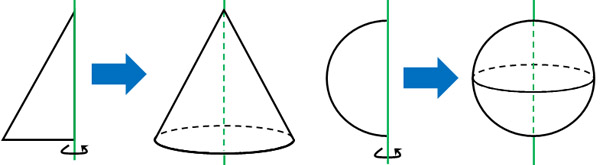
先ほど、長方形の回転体が円柱になると解説しました。一方で三角形の回転体は円錐になります。半円の回転体は球になります。
三角形や長方形を回転させるとき、必ず底面は円になります。一方で半円の回転体については、底面は存在しません。ただ回転体がカーブのある図形になるのは同じです。
円柱や円錐、球の公式を利用して計算する
回転体では、このようにして空間図形にて立体を考えます。その後、公式を利用して問題を解くようにしましょう。
円柱を計算する方法は既に理解していると思います。底面積に高さを掛けると、円柱の体積を出すことができます。また円錐では、円柱の体積を3分の1にすることで計算できます。
- 円柱の体積 = 底面積 × 高さ
- 円錐の体積 = 底面積 × 高さ × 1/3
それに対して、表面積はそれぞれの底面積と側面積を計算した後、足すようにしましょう。
球の場合についても、球の体積や表面積を出す公式を利用しましょう。球の計算は頻度が低いものの、公式を覚えていない場合は問題を解くことができません。球の問題を解きたい場合、以下の公式を覚えるようにしましょう。
・球の体積の公式

半径が分かる場合、公式に数字を代入することで球の体積を計算できます。
・球の表面積の公式

同じように、半径が分かる場合は表面積の公式に代入しましょう。回転体の球の表面積を計算することができます。
応用問題は図形の組み合わせ
こうした回転体の応用問題としては、図形の組み合わせが出されます。複数の異なる図形が存在するため、回転体の形が複雑になるのです。
例えば、以下の図形の回転体を考えてみましょう。
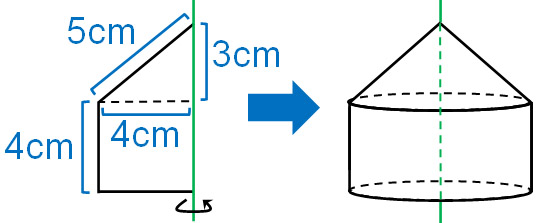
この図形では、三角形と四角形が混じっています。このような図形の場合、回転体では円錐と円柱の2つが混ざります。そうしたとき、図形を分けて体積や表面積を計算するようにしましょう。
・体積の計算
円錐と円柱でそれぞれ計算しましょう。円錐の体積は以下になります。
- \(4×4×π×3×\displaystyle\frac{1}{3}=16π\)
また、円柱の体積は以下になります。
- \(4×4×π×4=64π\)
円錐と円柱の体積を足すことで、答えは「\(16π+64π=80π\)cm3」と分かります。
・表面積の計算
表面積の計算では展開図を考える必要があります。つまり完成される空間図形を考えた後、平面に直すのです。以下のようになります。
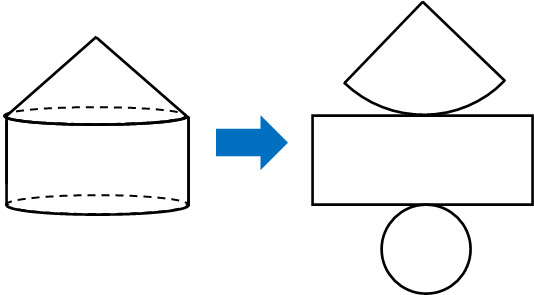
それぞれの面積を計算した後、足すようにしましょう。以下のようになります。
- 扇形の面積:\(5×4×π=20π\)
- 長方形の面積:\(8×π×4=32π\)
- 円の面積:\(4×4×π=16π\)
なお、扇形の面積は「円錐の側面積 = 母線 × 底面の半径 × \(π\)」の公式を使っています。立体の表面積の答えは、これらの面積を足すことで\(68π\)cm2になります。
- \(20π+32π+16π=68π\)
平面が軸から離れた回転体の形
ちなみに回転体を作るとき、平面が軸から離れているケースがあります。その場合、空洞をもつ回転体が作られます。
長方形の回転体は円柱になることを説明しました。一方で長方形が回転する直線から離れている場合、回転体は以下のようにドーナツ型となります。
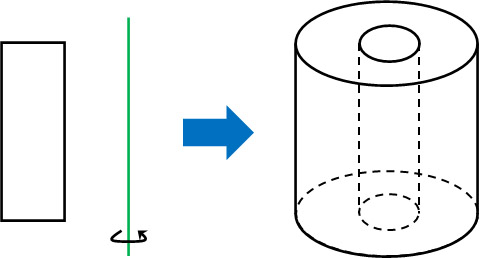
この図形の体積や表面積を計算する場合、2つの円柱を考慮しなければいけません。いずれにしても、回転軸から平面が離れている場合、空洞ができると考えましょう。
練習問題:回転体の体積と表面積
Q1. 次の図形について、直線を軸として一回転してできる図形の体積と表面積を計算しましょう。なお、円周率は\(π\)とします。
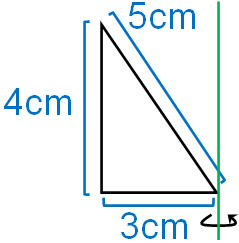
A1. 解答
この図形の回転体は以下のようになります。
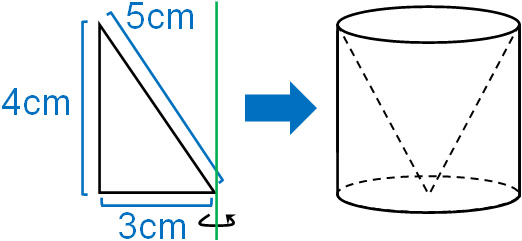
回転体の計算では、円錐と円柱を組み合わせた図形の計算が頻繁に出題されます。この図形では、円柱の中に円錐が存在します。そこで、円柱と円錐をそれぞれ分けて計算しましょう。
・体積の計算
円柱から円錐を引くと、体積を出すことができます。円柱の体積は以下になります。
- \(3×3×π×4=36π\)
一方で円錐の体積は以下になります。
- \(3×3×π×4×\displaystyle\frac{1}{3}=12π\)
そのため、立体の体積は\(24π\)cm3になります。
- \(36π-12π=24π\)
・表面積の計算
計算方法としては、「三角形と四角形の回転体」と同じです。展開図を考えると、扇形と長方形と円の3つの図形が表れます。そこで、それぞれの面積を計算しましょう。
- 扇形の面積:\(5×3×π=15π\)
- 長方形の面積:\(6×π×4=24π\)
- 円の面積:\(3×3×π=9π\)
それぞれの面積を足すと\(48π\)cm2になります。
- \(15π+24π+9π=48π\)
空間図形で回転体の基本を学ぶ
中学数学で学ぶ空間図形では、回転体という概念を学びます。一つの平面が存在し、軸を一回転させたときにできる空間図形が回転体です。
複雑な回転体の場合、高校数学の積分を利用しなければ問題を解くことができません。一方で三角形や四角形など、単純な図形の回転体であれば、積分を利用しなくても問題を解くことができます。そこで、円錐や円柱、球の公式を利用して計算しましょう。
応用問題では、複数の図形が組み合わさることになります。または、軸から図形が離れることもあります。ただ、基本的な考え方は同じです。
空間図形の中では、回転体の体積と表面積を出す問題は難易度が高いです。どのような回転体ができるのか想像し、体積と表面積を計算できるようにしましょう。






