高校物理では力学を学びます。力学で最初に学ぶ内容が変位(距離)・速度・加速度です。小学校の算数や中学校の数学で学ぶ速度は等速直線運動です。ただ実際には速度が変化するため、物理では速度が変化するときの様子を学ばなければいけません。
また物理では力の向きが重要です。正と負のどちらの方向に力が加わっているのかを見極めることにより、符号を決定できます。
なお変位・速度・加速度を学べば、等加速度直線運動を理解できます。等加速度直線運動には3つの公式があり、物理の問題を解くためには必ず公式を覚えなければいけません。このとき、\(v-t\)グラフを利用すれば等加速度直線運動の公式を理解しやすいです。
それでは、物体が動いた距離や速度、加速度を計算するにはどうすればいいのでしょうか。加速度の概念や等加速度直線運動の公式の使い方を解説していきます。
もくじ
変位(距離)・速度・加速度の違い
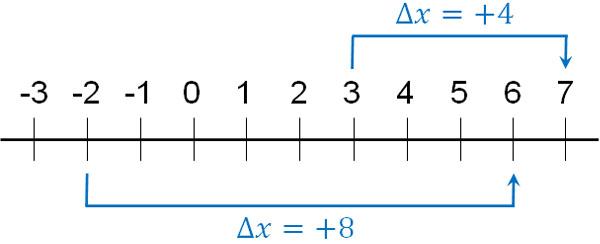
小学校の算数や中学の数学で距離と速度の関係を学びます。変位とは、動いた距離を指します。物理では変化量を表すときの記号として\(Δ\)を利用します。また、物理では距離の変化量を\(x\)で表します。そのため、変位は\(Δx\)で表されます。
例えば+3mから+7mの位置へ移動した場合、変位\(Δx\)は+4mです。また-2mから+6mへ移動した場合、変位\(Δx\)は+8mです。
速度を得るためには、移動に必要だった時間で割ります。例えば2秒で+8mを進んだのであれば、秒速4m/sです。
\(8÷2=4\)
なお時間というのは、どの時間を測定するのかが重要です。例えば2秒経過というのは、0秒から2秒までを測定したのかもしれませんし、7秒から9秒までを測定したのかもしれません。そこで物理では、時間\(t\)の変化量を利用します。
先ほど説明した通り、変化量は記号\(Δ\)を利用して表します。そのため、時間tの変化量は\(Δt\)です。つまり、速度\(v\)を以下のように表すことができます。
- \(v=\displaystyle\frac{Δx}{Δt}\)
この公式を覚える必要はなく、小学校で速度の計算を学んでいる場合、すべての人が公式の意味を理解できます。物理の教科書に\(v=\displaystyle\frac{Δx}{Δt}\)と記されていると難しいように思えます。ただ実際には、小学校で学ぶ速度の計算を記号や文字に置き換えているにすぎません。
等速直線運動と等加速度直線運動
なお小学校や中学校で学ぶ速度の計算では、常に速度が同じです。この場合、等速直線運動と呼ばれます。
ただ実際には、速度が同じであるケースは少ないです。例えば車を発進させるとき、徐々に速度が速くなります。またボールを斜面で転がす場合、徐々にスピードが速くなります。
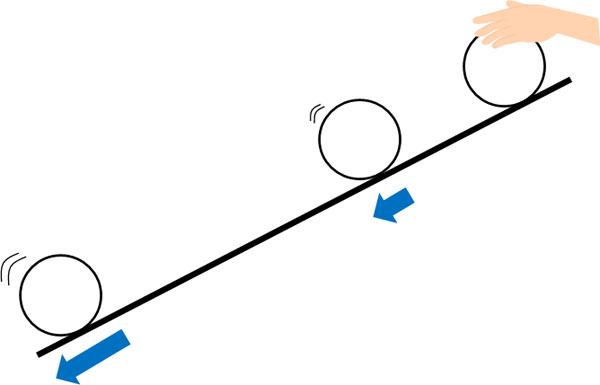
つまり、速度が常に変化しているのです。そこで物理では、時間当たりの速度変化を表す指標として加速度を利用します。
・物理で学ぶ加速度\(a\)の計算
それでは、加速度はどのように計算すればいいのでしょうか。例えば静止している状態から、2秒後に10m/sの速度になったとします。この場合、1秒ごとに5m/s速度が上昇しているとわかります。1秒後に5m/sとなり、2秒後に10m/sになります。
加速度は速度の変化を表します。単位時間あたりにどれだけ速度が変化したのかを計算すればいいため、速度の変化量\(Δv\)を時間の変化量\(Δt\)で割ることによって加速度\(a\)を得ることができるのです。
- 加速度\(a=\displaystyle\frac{Δv}{Δt}\)
加速度を生じる場合、物体のスピードは常に速くなります(負の加速度の場合、スピードは遅くなります)。また加速度が一定の場合、等加速度直線運動と呼ばれます。
なお速度の単位はm/sであり、時間の単位はs(秒)です。加速度は速度を時間で割るため、単位はm/s2となります。
物理では正と負の向きが非常に重要となる
なお物理では正と負の向きが重要になります。計算をして答えを得るとき、符号がプラスなのかマイナスなのかを判断しなければいけません。このとき、必ず頭の中で符号の向きを想像しましょう。
例えば車に乗って加速しているとき、速度と加速度はプラスです。例えば40m/sで走っているとき、+3m/s2の加速度を加えると、2秒後には46m/sになります。
\(40+3×2=46\)
それに対して、40m/sで走っているとき、ブレーキをかけて-3m/s2の加速度を加える場合の速度はどうなるでしょうか。この場合、2秒後には34m/sになっています。
\(40-3×2=34\)
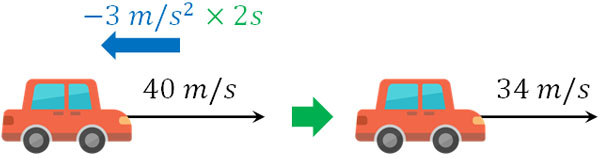
車が走っている方向に対して、逆向きの加速度が加わるため、加速度はマイナスになります。物理では変位(距離の変化)や速度、加速度がマイナスになることがひんぱんにあります。見分け方としては、最初の設定した向きと同じなのか、それとも逆向きなのかを確認しましょう。
またここまで解説した内容を理解すると、速度と加速度はまったく異なる概念であるとわかります。先ほどの事例でわかる通り、速度がプラスであっても、加速度がマイナスになるケースはひんぱんにあるからです。
車を例とすると、加速度が常にマイナスの場合、速度は徐々に遅くなって最終的に車は止まります。また加速度は常にマイナスであるため、車が停止した後はバックし始めます。
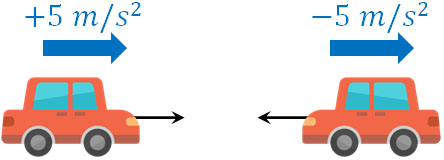
そのため物理の問題を解く場合、最初に正の向きを決めましょう。例えば車に対して東向きに5m/s2の加速度を加える場合、符号はプラスでしょうか、それともマイナスでしょうか。
車が東に向かって進んでいた場合、東向きは正です。そのため、加速度は+5m/s2です。一方で車が西向きに進んでいた場合、西向きが正です。そのため、東向きの加速度は-5m/s2です。最初に向きを決めれば、「符号を正にすればいいのか、それとも負にすればいいのか」が決まります。
なお車を運転するとき、常に加速し続けることはありません。加速をずっと続けた場合、現実的にはスピード違反によって逮捕されます。そのため一定の加速度(等加速度直線運動)によって速度を上昇させた後、速度を一定の状態(等速直線運動)にします。
世の中の自然現象を学ぶのが物理です。そのため、実際に物体が動くときの様子を頭の中でイメージしましょう。そうしなければ、物理の問題を解くのが難しくなります。
\(v-t\)グラフ:傾きや面積、変位の関係
それでは、速度と時間の関係をグラフに表してみましょう。タテ軸を速度、横軸を経過時間とする図を作ります。速度\(v\)と時間\(t\)を利用するため、このグラフを\(v-t\)グラフといいます。
例として、以下の\(v-t\)グラフを考えてみましょう。
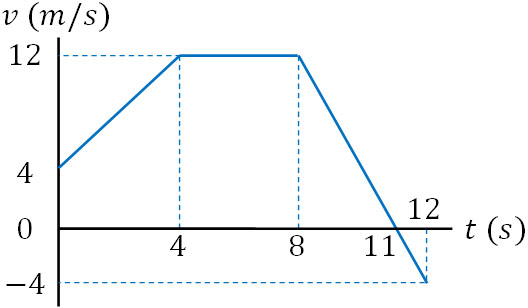
このグラフは何を意味しているのでしょうか。物理は世の中の現象を表しており、グラフの意味を理解しないと物理の問題を解くことはできません。例えば、車を運転している場面を考えましょう。
0~4秒の間では、速度は一定の割合で増加しています。同じ割合で速度増加が起こっているため、加速度は一定です。言い換えると、同じ加速度によって徐々に速度が上がっている状態(等加速度直線運動が起きている状態)です。アクセルによって速度上昇している状態ともいえます。
それに対して、4~8秒の間では速度は一定です。つまり加速度は0であり、等速直線運動になっています。
一方、8~11秒の間では徐々に速度が遅くなり、最終的に速度が0になっています。マイナスの加速度によって減速している状態であり、車にブレーキをかけています。
また11~12秒では、速度はマイナスになっています。つまり、最初の方向に対して反対向きに進んでおり、車をバックさせている状態です。また速度は0m/sから-4m/sに変化しており、バックで進む速度は加速しています。
グラフから、これらの情報を読み取るようにしましょう。物理を理解するとき、必ず世の中の現象とひもづける必要があります。そうしなければ、物理の問題を解くのは難しいです。
\(v-t\)グラフの傾きは加速度\(a\)を表す
それでは、先ほどの\(v-t\)グラフを利用して加速度を計算しましょう。
・0~4秒の間
0~4秒の間では、時間の変化量\(Δt\)は4sです。また、速さは4m/sから12m/sへ変化しています。そのため、速さの変化量\(Δv\)は8m/sです。4秒かけて8m/sの変化であるため、加速度\(a\)は2m/s2です。
なお速さの変化量\(Δv\)と時間の変化量\(Δt\)を利用する計算式は以下になります。
\(a=\displaystyle\frac{12-4}{4-0}=2\)
・4~8秒の間
速度が一定のため、加速度\(a\)は0です。
・8~12秒の間
8~12秒では4秒が経過しています。つまり、時間の変化量\(Δt\)は4sです。また速度は12m/sから-4m/sに変化しているため、速さの変化量\(Δv\)は-16m/sです。4秒かけて-16m/sの変化であるため、加速度\(a\)は-4m/s2です。
速さの変化量\(Δv\)と時間の変化量\(Δt\)を利用し、計算式で表すと以下のようになります。
\(a=\displaystyle\frac{-4-12}{12-8}=-4\)
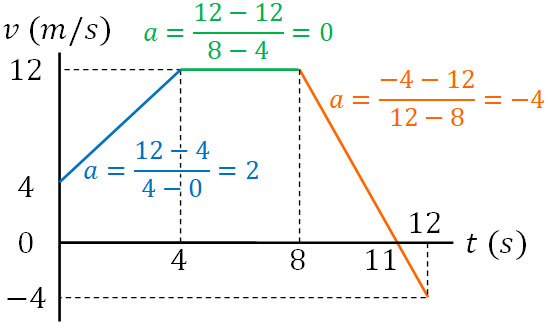
重要なのは、「グラフの傾きが加速度\(a\)である」という事実です。等加速度直線運動では加速度が一定です。そのため、等加速度直線運動ではグラフの傾きが加速度になるのです。
なお、わかりやすく一次関数での傾きを利用して加速度を解説しました。ただ実際には、グラフの形が二次関数や三次関数であっても、グラフの傾きは加速度になります。速さが変化するとき、傾きが必ず加速度になる事実は非常に重要なので覚えましょう。
\(v-t\)グラフの面積は距離\(x\)を表す
先ほど、グラフの傾きと加速度の関係を解説しました。次はグラフの面積に着目しましょう。4~8秒の間では、速度が一定です。速度が同じ場合(等速直線運動の場合)、経過時間をかけることによって変位(移動距離)を計算できます。
4~8秒の間では12m/sで4秒経過しているため、移動した距離は48mです。
\(12×4=48\)
重要なのは、先ほどの計算式はグラフの面積を計算しているのと意味が同じという点です。つまり移動距離というのは、\(v-t\)グラフの面積を指します。
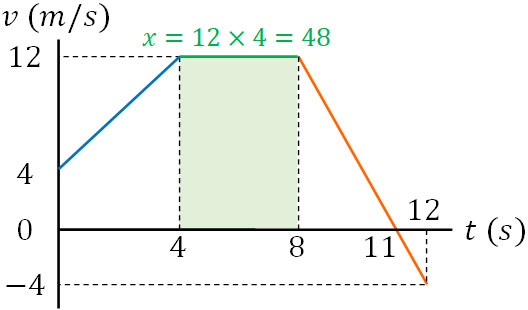
そこで、ほかの部分についても面積を計算し、移動距離を得ましょう。以下のようになります。
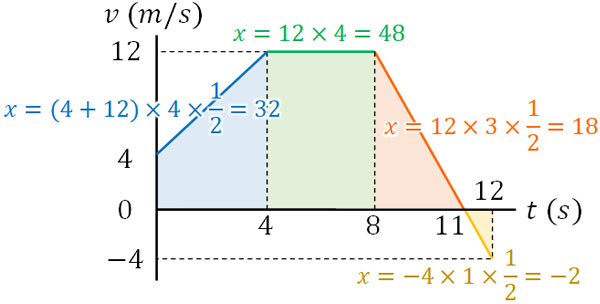
すべての面積を足すと96になります。つまり、合計の移動距離は96mです。
公式を覚えても物理で問題を解くことはできません。それよりも、グラフや公式の意味を理解することが重要です。「\(v-t\)グラフで傾きは加速度\(a\)を表し、面積は移動距離\(x\)を表す」という事実は非常に重要です。
等加速度直線運動の公式
ここまでの内容を理解したうえで等加速度直線運動の公式を覚えましょう。等加速度直線運動の公式は以下の3つです。
- \(v=v_0+at\)
- \(x=v_0t+\displaystyle\frac{1}{2}at^2\)
- \(v^2-v_0^2=2ax\)
それでは、これらの公式は何を意味しているのでしょうか。力学の問題を解く場合、この3つの公式がメインになります。そのため、何度も問題を解いていれば自動的に覚えます。ただそれでは意味がなく、公式の性質を学びましょう。
等加速度直線運動の公式で最も重要な公式は\(v=v_0+at\)です。\(v_0\)は初速度を意味します。静止している状態であれば、初速度\(v_0\)は0です。ただ、既にある程度の速さで動いていることはよくあります。そこで、速さを計算するときは最初に初速度\(v_0\)を設定します。
また先ほど説明した通り、時間\(t\)が経過するに伴い、加速度\(a\)の分だけ速度が上昇します。つまり、\(t\)秒後の速度増加分は\(a×t\)です。そのため、速さ\(v\)を得るための公式は\(v=v_0+at\)となるのです。
例えば初速度4m/s、加速度1m/s2の等加速度直線運動では以下のグラフになります。
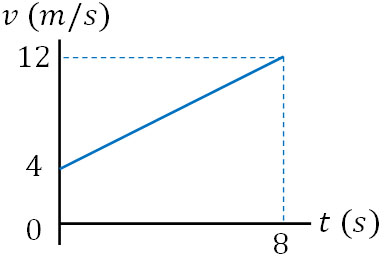
初速度4m/sであるため、最初は4m/sでスタートします。また加速度1m/s2であるため、1秒経過するごとに速度は1m/sずつ上昇します。そのため、例えば8秒後では、速度の上昇分は8m/sです。そこで初速度4m/sと上昇した速度8m/sを足すと、12m/sになります。
\(v=v_0+at\)
\(v=4+1×8=12\)
このように確認すると、なぜ速さ\(v\)を得る公式が\(v=v_0+at\)となるのか理解できます。
面積を計算する公式が\(x=v_0t+\displaystyle\frac{1}{2}at^2\)
次に\(x=v_0t+\displaystyle\frac{1}{2}at^2\)を確認しましょう。前述の通り、\(v-t\)グラフの面積を計算すると、移動距離\(x\)を得られます。
つまり\(x=v_0t+\displaystyle\frac{1}{2}at^2\)というのは、\(v=v_0+at\)を利用して面積を計算しています。そこで図を利用し、公式が何を意味しているのか確認しましょう。
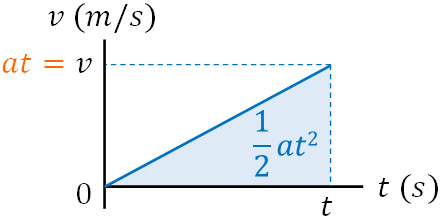
まず、\(t\)秒後の移動距離\(x\)はいくらでしょうか。初速度が\(v_0\)なのであれば、\(t\)秒後の距離(面積)は\(v_0×t\)になります。

次に、加速度\(a\)が一定で\(t\)秒が経過したときの距離(面積)を計算しましょう。
三角形の面積はたてと横をかけ、2で割ることによって得られます。横軸は経過時間\(t\)であるとわかります。
またたて軸は速度\(v\)です。速度\(v\)は加速度\(a\)と経過時間\(t\)をかけることで得られます。加速度\(a\)m/s2は「1秒ごとに\(a\)m/sずつ速度が速くなる」ことを意味しています。そのため、たて軸(速度)は\(a×t\)です。
たて軸(速度)が\(at\)であり、横軸(時間)が\(t\)であるため、三角形の面積(距離)は以下のようになります。
- \(\displaystyle\frac{1}{2}at^2\)
そこで、初速度\(v_0\)での移動距離(面積)と加速度\(a\)によって速度が徐々に早くなるときの移動距離(面積)を足しましょう。以下のようになります。
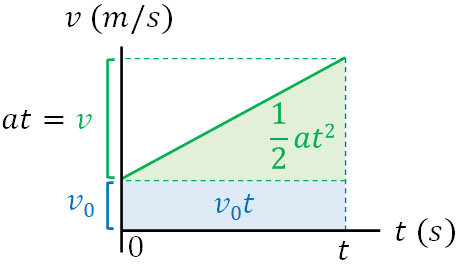
こうして\(v=v_0+at\)を利用し、面積を計算することで\(x=v_0t+\displaystyle\frac{1}{2}at^2\)の公式を得ることができました。
力学の計算をするとき、多くの人は公式の意味を理解していません。公式を暗記し、計算するのです。ただ、これでは物理の本質を理解できないため、必ず公式が何を意味しているのか学びましょう。
・数学で学ぶ微分・積分によって公式を得られる
ここまでの解説で重要なのは、「速度\(v\)に対してグラフの傾きを計算すれば、この傾きが加速度\(a\)となり、グラフの面積を計算すれば距離\(x\)を求められる」という事実です。
等加速度直線運動では、加速度\(a\)は一定です。この場合、繰り返しになりますが、速度\(v\)と距離\(x\)は以下の公式で計算できます。
- \(v=v_0+at\)
- \(x=v_0t+\displaystyle\frac{1}{2}at^2\)
数学では微分と積分を学びます。微分とは、グラフの傾きを得る操作を指します。前述の通り、\(v-t\)グラフの傾きが加速度\(a\)です。言い換えると、速度\(v\)を微分すると加速度\(a\)となります。
また積分とは、面積を計算する操作を指します。前述の通り、\(v-t\)グラフの面積が距離\(x\)です。言い換えると、速度\(v\)を積分すると距離\(x\)となります。つまり、距離・速度(速さ)・加速度には以下の関係性があります。
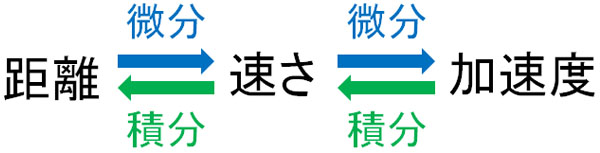
もしあなたが微分・積分を既に学んでいる場合、\(v=v_0+at\)を微分してみましょう。そうすると、加速度\(a\)が一定であると計算できます。
また\(v=v_0+at\)を積分してみましょう。そうすると、\(x=v_0t+\displaystyle\frac{1}{2}at^2\)を得ることができます。他には、\(x=v_0t+\displaystyle\frac{1}{2}at^2\)を微分すると\(v=v_0+at\)となります。
重要なのは、微分と積分を利用できることではありません。グラフの傾きと面積を利用すれば、距離・速度・加速度の関係を説明できる事実です。
\(v^2-v_0^2=2ax\)の解説と式の変形
なお、\(v=v_0+at\)と\(x=v_0t+\displaystyle\frac{1}{2}at^2\)を利用し、\(t\)を消すと\(v^2-v_0^2=2ax\)を得ることができます。
\(v^2-v_0^2=2ax\)に特別な意味はありません。ただ計算問題を解くとき、公式として\(v^2-v_0^2=2ax\)を利用するケースはひんぱんにあります。公式に特別な意味はないものの、力学の計算問題を解くためには公式を覚える必要があります。
それでは、\(v^2-v_0^2=2ax\)を導き出しましょう。\(v=v_0+at\)を利用し、以下のように変形します。
\(v=v_0+at\)
\(at=v-v_0\)
\(t=\displaystyle\frac{v-v_0}{a}\) (\(a≠0\))
次に、\(t=\displaystyle\frac{v-v_0}{a}\)を\(x=v_0t+\displaystyle\frac{1}{2}at^2\)に代入します。
\(x=\displaystyle\frac{v_0(v-v_0)}{a}+\displaystyle\frac{a}{2}·\displaystyle\frac{(v-v_0)^2}{a^2}\)
\(x=\displaystyle\frac{1}{2a}(v^2-v_0^2)\)
\(v^2-v_0^2=2ax\)
こうして、公式を導き出すことができました。
他の公式とは異なり、\(v^2-v_0^2=2ax\)では経過時間\(t\)を利用していません。そのため時間\(t\)がわからない場合、この公式を利用しましょう。
等加速度直線運動の公式を利用する練習問題
それでは、実際に等加速度直線運動の公式を利用して問題を解いてみましょう。以下の問題の答えは何でしょうか。
- 初速度10m/sで右向きに動いている物体があります。物体は等加速度直線運動で動いており、7秒後の速度は左向きに4m/sでした。
- 物体の加速度はいくらでしょうか。
- 9秒後の物体の場所はどこでしょうか。
- 速度が0になるときの位置と時間はいくらでしょうか。
- 最初の位置から右に16mの位置を通過するときの速度はいくらでしょうか。
物理の問題を解く場合、どのような場面なのか必ず想像しましょう。そうしなければ、問題を解くことができません。最初は右向きに物体(例えばボール)を発射させ、7秒後は左向きに動いているという状態は、以下のような坂を利用している場面と想像できます。
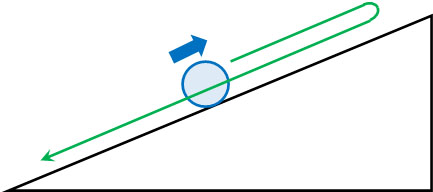
この場合、時間経過と共に速度は減少します。つまり、加速度はマイナスでなければいけません。またどこかの時点で静止し、速度が0になります。その後、左向きに動き始めます。加速度はマイナス(左向き)であるため、時間経過と共に左向きのスピードは速くなります。
このような場面を想像すれば、力学の問題を解くことができます。
1) 物体の加速度はいくらでしょうか
初速度(10m/s)と7秒後の速度(-4m/s)がわかっているため、公式を利用して計算しましょう。
\(v=v_0+at\)
\(-4=10+7a\)
\(7a=-14\)
\(a=-2\)
物体の加速度は-2m/s2です。
2) 9秒後の物体の場所はどこでしょうか
加速度がわかっているため、\(x=v_0t+\displaystyle\frac{1}{2}at^2\)に代入しましょう。
\(x=v_0t+\displaystyle\frac{1}{2}at^2\)
\(x=10×9+\displaystyle\frac{1}{2}(-2)9^2\)
\(x=90-81\)
\(x=9\)
9秒後、物体の位置は右に9mです。
3) 速度が0になるときの位置と時間はいくらでしょうか
加速度はマイナスであるため、どこかの時点で物体の速度は瞬間的に0となり、静止します。そこで速度\(v=0\)を代入しましょう。
\(v=v_0+at\)
\(0=10-2t\)
\(t=5\)
5秒後、物体の速度は0になります。
4) 最初の位置から右に16mの位置を通過するときの速度はいくらでしょうか。
時間\(t\)が記されていないため、\(v^2-v_0^2=2ax\)を利用しましょう。
\(v^2-v_0^2=2ax\)
\(v^2-10^2=2×-2×16\)
\(v^2=36\)
\(v=6,-6\)
こうして、答えは6m/sと-6m/sです。加速度はマイナスであるため、物体は同じ場所を2回通過します。そのため右に16mの場所について、最初に右向きに6m/s、少し遅れて左向きに6m/sで通過します。
等加速度直線運動の公式を利用し、変位・速度・加速度を計算する
高校物理で最も基本的な力学の内容が等加速度直線運動です。力学を学ぶとき、最初に習う内容の一つになります。そこで加速度の概念を学び、変位と速度の関係性を把握しましょう。このとき、向きに注意して符号を決める必要があります。
等加速度直線運動を理解するとき、必ず利用されるのが\(v-t\)グラフです。たて軸を速度\(v\)に設定することで、\(v-t\)グラフを作ることができます。このとき傾きが加速度\(a\)になり、面積が距離\(x\)になります。
これらを理解すれば、等加速度直線運動の公式が何を意味しているのかわかります。等加速度直線運動の公式は3つあり、それぞれ何を意味しているのか理解しましょう。
物理では公式の意味を理解するのが重要です。また問題文が出されたとき、どのような現象が起こっているのか想像しましょう。等加速度直線運動は力学の最初で学ぶものの、理解しなければいけない概念は多く、ここまで解説したことを学びましょう。






