磁石とコイルを利用することにより、電気を発生させることができます。この現象を電磁誘導といいます。
火力発電や風力発電など、発電所でどのように電気を得ているかというと、電磁誘導を利用しています。電磁誘導によって新たに電気を発生させ、私たちは日々の生活で電気を利用できるのです。そのため、電磁誘導は非常に重要な分野の一つです。
電磁誘導を学ぶとき、電流と電圧の向きがわかるようになりましょう。また、電圧の大きさを計算できるようになりましょう。そのために必要な知識がレンツの法則とファラデーの電磁誘導の法則です。
それでは、なぜ磁石とコイルによって電気が発生するのでしょうか。また、磁場と電圧にはどのような関係があるのでしょうか。電磁誘導が起こる原理や公式の意味、計算の方法を解説していきます。
もくじ
コイルと磁石で電流を生じる:誘導起電力と誘導電流
導線をぐるぐる巻きにした道具をコイルといいます。コイルに対して磁石を近づけたり、遠ざけたりすると電流が発生します。
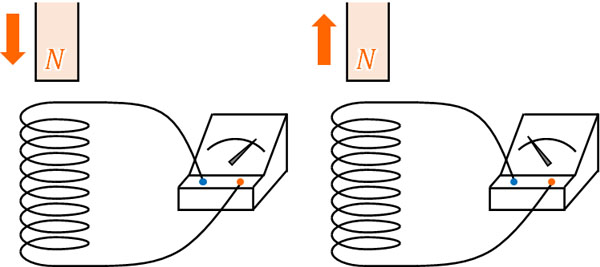
方法は簡単であり、以下のようにコイルと磁石を用意し、磁石を動かしましょう。そうすると、検流計の針が動きます。検流計の針が動くというのは、電流が発生したことを意味します。
通常、電流が流れるためには電源に接続しなければいけません。ただ電源(電池)を利用しなくても、何もない状態から電流を得ることができるのです。この現象が電磁誘導です。
電磁誘導によって電流が流れるとき、電圧も発生します。そこで、以下の言葉を覚えましょう。
- 誘導起電力:電磁誘導によって発生した電圧
- 誘導電流:電磁誘導によって発生した電流
電池に電気量を蓄えるにしても、元となる電流を発生させなければいけません。そこで電磁誘導を利用して発電し、何もない状態から電流と電圧を得るのです。
磁石を動かす向きと誘導電流の向き
それでは磁石を動かすとき、検流計の針はどのように動くのでしょうか。実際に電磁誘導の実験をすると、磁石を近づけるのか、それとも遠ざけるのかによって検流計の針の向きが異なります。
例えば先ほどの図であれば、N極を近づけることによって誘導電流が発生する場合、検流計の針は右に動きます。一方でN極を遠ざける場合、検流計の針は左に動きます。
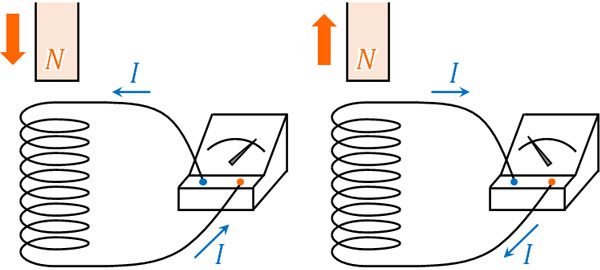
重要なのは、同じN極を利用する場合であっても、コイルに近づける場合とコイルから遠ざける場合では誘導電流の向きが異なるという事実です。電流の向きが反対になるため、誘導起電力の向きも当然ながら反対になります。
また、S極を利用する場合についても電磁誘導が起こります。コイル周辺の磁場が変化する場合、電磁誘導が起こると理解しましょう。
なおN極とS極では、磁場の向きが逆になります。そのため、電磁誘導によって発生する電流の向きも逆になります。そのため先ほどのコイルであれば、S極を近づけると誘導電流によって検流計の針は左に動きます。一方、S極を遠ざけると検流計の針は右に動きます。
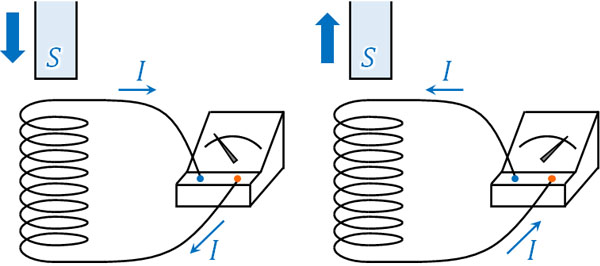
このように近づけたり遠ざけたりするのがN極なのか、それともS極なのかによっても電流の向きが異なることに注意しましょう。
レンツの法則:変化を打ち消すように電流が流れる
それでは、誘導電流と誘導起電力の向きはどのように判断すればいいのでしょうか。電流と電圧の向きを確認するとき、利用される法則にレンツの法則があります。以下がレンツの法則になります。
- 外部磁場の変化を打ち消すように誘導電流が流れる
恐らく理解できないと思いますので、レンツの法則が何なのか詳細に解説していきます。
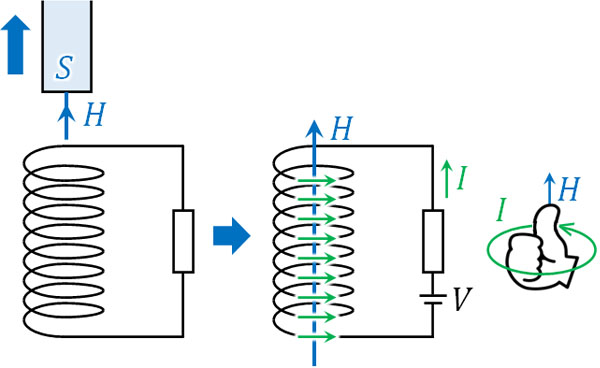
コイルというのは、変化を嫌います。磁石を近づけたり遠ざけたりする場合、コイル周辺の磁場が変化します。そこで、磁場の変化を打ち消すようにコイルに電流が発生するのです。例えばN極をコイルに近づける場合、以下のようにN極から磁場\(H\)が発せられています。
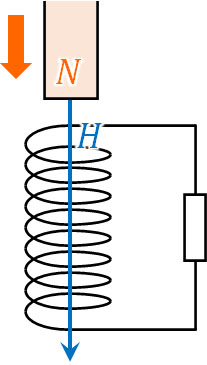
そこで、この磁場とは反対向きに磁場を発生させれば、磁石(外部磁場)による変化を抑えることができます。電流が発生すれば、新たな磁場が生まれます。コイルで電流が発生する理由は、磁場を生み出すことによって外部磁場の変化を打ち消そうとするからなのです。
そのため先ほどの例であれば、コイルは以下のように磁場を発生させればいいとわかります。
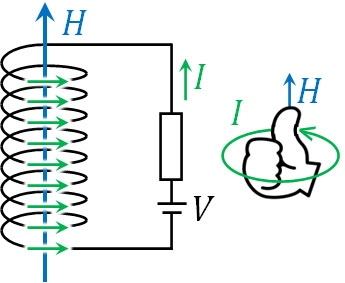
また、この磁場を発生させるためには、上図のように電流\(I\)が流れればいいとわかります。磁石による磁場に対して、逆向きに新たな磁場が発生するように電流が流れ、外部磁場の影響を弱めるのです。同時に、誘導起電力\(V\)を生じます。これがレンツの法則です。
なお電磁誘導によって発生する電流の向きについては、右ねじの法則を利用することで確認しましょう。
磁石を遠ざけるときの電磁誘導と右ねじの法則
それでは先ほどのコイルについて、N極を遠ざける場合はどのように考えればいいのでしょうか。N極を遠ざけるため、コイル内の磁場は弱まります。そのため、コイル内の磁場を強めるように磁場を発生させればいいとわかります。
この場合、先ほどとは逆の現象が起こります。下図のように電流を発生させ、コイル周辺の磁場を強めるように電磁誘導が起こります。
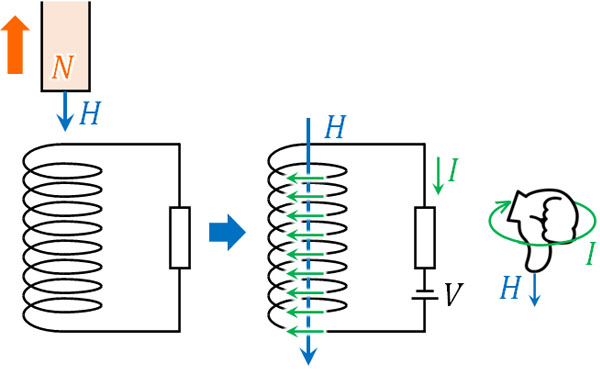
右ねじの法則を利用すれば、コイル周辺の磁場を強めるときの電流の向きがわかります。
N極とS極では反対の現象が起こる
またN極ではなく、S極を利用する場合も前述の通り逆の現象が起こります。磁場の向きはN極からS極となっています。そのため、S極では先ほどとは逆に向きの磁場が発生しています。
S極を近づける場合、磁場はS極に向かって動きます。そこで、この向きとは反対方向にコイルは磁場を発生させます。
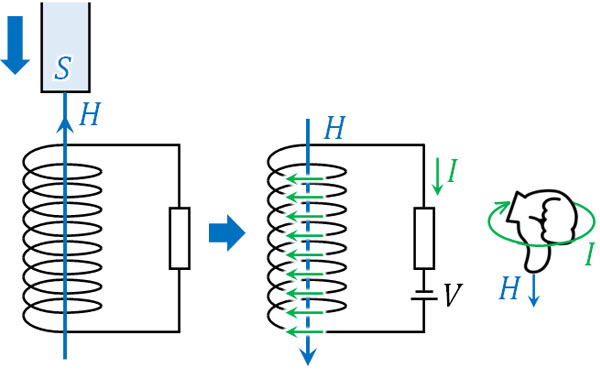
それに対してS極を遠ざける場合、S極に向かう磁場が弱くなります。そこで、S極へ向かう磁場を強めるように電流が発生します。
このように利用する磁石の部分がN極なのかS極なのかによって、発生する誘導電流と誘導起電力の向きが変化します。
・磁場が変化するときのみ電流が流れる
なお電磁誘導によって磁場が発生するのは、磁場が変化するときのみです。つまり、磁石をコイルに対して近づける、または遠ざけるときに電流が発生します。
磁石をコイルに近づけた後、静止させると、電流は発生しなくなります。コイルは磁場の変化を嫌うものの、新たな磁場の環境に慣れる性質があるのです。
磁束密度\(B\)と面積\(S\)により、磁束\(Φ\)を得る
それでは、電磁誘導によって発生する電圧を計算するにはどのようにすればいいのでしょうか。これを学ぶ前に、事前知識として磁束を解説します。
磁場\(H\)と透磁率\(μ\)をかけることにより、磁束密度\(B\)を得ることができます。物体によって、磁場に対する影響度合いが異なります。例えば鉄は磁石にくっつくものの、アルミニウムは磁石にくっつきません。そこで磁場に加えて、物体の磁場に対する影響度合いを考慮した値が磁束密度です。
磁束密度は磁束線を利用して描くことができます。磁束密度が\(B\)[T]の場合、1m2あたり\(B\)[本]の磁束線を描くことができます。そのため面積が\(S\)[m2]の面では、面を垂直に貫く磁束線の数は\(BS\)[本]です。
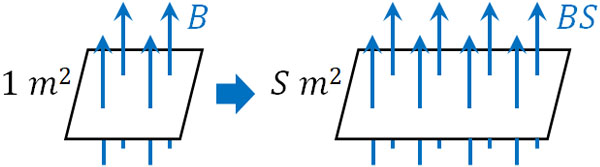
このとき、特定の面積を貫く磁束線の数を磁束といいます。磁束\(Φ\)は以下の式によって計算できます。
- \(Φ=BS\)
電磁誘導で誘導起電力の計算をするとき、磁束\(Φ\)を利用します。そのため、磁束とは何かを事前に学びましょう。
ファラデーの電磁誘導の法則と公式
それでは、電磁誘導によって発生する誘導起電力\(V\)を計算できるようになりましょう。誘導電流や誘導起電力が発生するとき、コイル周辺の磁場の変化が大きいほど、発生する電流や電圧は大きくなります。
当然、強力な磁場(磁束密度)を発する磁石を利用するほうが磁場の変化は大きくなり、発生する誘導起電力は大きくなります。また同じ磁石を利用する場合であっても、磁石を出し入れするスピードが速いほど大きな誘導起電力を生じます。
それに加えて、コイルの巻数も発生する電圧にとって重要な要素です。当然、コイルの巻数が多いほど発生する電圧は大きくなります。そこで、これらの事実を用いて公式にしましょう。
19世紀の科学者・ファラデーが発見した法則の一つにファラデーの電磁誘導の法則があります。彼は非常に多くの法則を発見した科学者であるため、「ファラデーの法則」では、何の法則を指しているのかわかりません。そのため、ファラデーの電磁誘導の法則という名前を利用しましょう。
電磁誘導について、彼は以下の法則を発見しました。
- 誘導起電力\(V\)はコイルの巻数\(N\)と1秒あたりの磁束変化\(\displaystyle\frac{ΔΦ}{Δt}\)に比例する。
これを数式に表すと以下のようになります。
- \(V=N\left|\displaystyle\frac{ΔΦ}{Δt}\right|\)
それでは、この式は何を意味しているのでしょうか。コイルの巻数\(N\)が多いほど、誘導起電力\(V\)は大きくなります。そのため、\(N\)をかけましょう。
また磁力が強いというのは、磁束\(Φ\)の値が大きいことを意味しています。ただ、どれだけの時間をかけて磁束の変化が起こったのかを考慮しなければいけません。このとき、\(Δt\)秒で磁束が\(ΔΦ\)の変化をするとき、1秒での磁束の変化は\(\displaystyle\frac{ΔΦ}{Δt}\)となります。
そこでコイルの巻数\(N\)と1秒での磁束変化\(\displaystyle\frac{ΔΦ}{Δt}\)をかけることにより、誘導起電力\(V\)を得られるのです。これがファラデーの電磁誘導の法則であり、公式で表すと\(V=N\left|\displaystyle\frac{ΔΦ}{Δt}\right|\)になります。
なお電流の向きについては、先ほど解説した通り、レンツの法則を利用して確認しましょう。
電磁誘導に関する練習問題
電磁誘導に関する練習問題を解くことで、どのように公式を利用すればいいのか学びましょう。以下の問題の答えは何でしょうか。
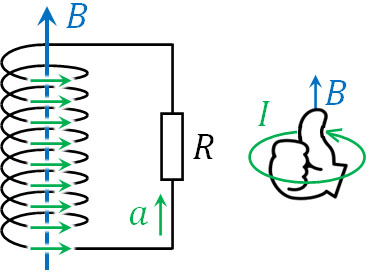
面積\(S\)、巻数\(N\)のコイルを利用して、抵抗\(R\)とつなぎました。磁束密度\(B\)を下のグラフのように変化させるとき、抵抗を流れる電流\(I\)と向き(\(a\)または\(b\))を求めましょう。
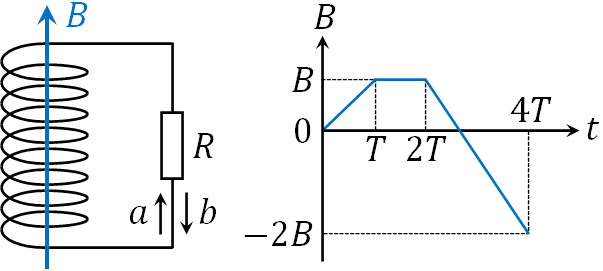
- \(0≦t≤T\)のときの電流\(I\)と向き
- \(T≦t≤2T\)のときの電流\(I\)と向き
- \(2T≦t≤4T\)のときの電流\(I\)と向き
1) \(0≦t≤T\)のときの電流\(I\)と向き
\(0≦t≤T\)のとき、時間変化は\(Δt=T\)です。また、磁束変化は\(ΔΦ=SB\)です。そのため、誘導起電力は\(V=\displaystyle\frac{NBS}{T}\)です。
オームの法則より、\(V=RI\)です。そのため、以下のように電流を計算できます。
\(V=RI\)
\(\displaystyle\frac{NBS}{T}=RI\)
\(I=\displaystyle\frac{NBS}{RT}\)
こうして、電流は\(I=\displaystyle\frac{NBS}{RT}\)とわかりました。
なお磁束密度\(B\)は下から上の向きであるため、電磁誘導ではその反対向きに磁場を発します。そこで右ねじの法則を利用すると、電流の向きは\(b\)とわかります。
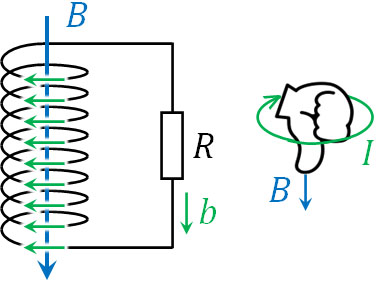
2) \(T≦t≤2T\)のときの電流\(I\)と向き
\(T≦t≤2T\)では磁場(磁束密度)の変化がないため、電流はゼロです。
3) \(2T≦t≤4T\)のときの電流\(I\)と向き
\(2T≦t≤4T\)のとき、時間変化は\(Δt=2T\)です。また、磁束変化は\(ΔΦ=-3SB\)です。そのため、誘導起電力は\(V=\displaystyle\frac{3NBS}{2T}\)です。
またオームの法則より、以下のように電流を計算できます。
\(V=RI\)
\(\displaystyle\frac{3NBS}{2T}=RI\)
\(I=\displaystyle\frac{3NBS}{2RT}\)
こうして、\(I=\displaystyle\frac{3NBS}{2RT}\)であると計算できました。
なお磁束密度の変化が\(-3B\)であるため、磁場は上から下の向きであるとわかります。そのため、磁場(磁束密度)による変化を和らげるためには、コイルは下から上の向きに磁場を発生させればいいとわかります。そのため、右ねじの法則より電流の向きは\(a\)です。
電磁誘導ではファラデーの電磁誘導の法則を利用して計算問題を解き、レンツの法則を利用して電流や電圧の向きを確認しましょう。
電磁誘導で重要なレンツの法則とファラデーの電磁誘導の法則
私たちは発電機によって得られた電気を利用しています。発電は電磁誘導によって行われており、磁石とコイルを用いて電気を発生させているのです。
コイルには、磁場の変化を嫌う性質があります。この性質を利用して電気を得るのが電磁誘導の原理です。レンツの法則を利用し、誘導電流と誘導起電力の向きを判断できるようになりましょう。このとき、必ず右ねじの法則を利用することになります。
また誘導起電力\(V\)を計算するとき、ファラデーの電磁誘導の法則を利用しましょう。コイルの巻数\(N\)、磁束変化\(ΔΦ\)、時間変化\(Δt\)を利用することにより、誘導起電力を得ることができます。
電磁誘導の基本がレンツの法則とファラデーの電磁誘導の法則です。磁石とコイルを利用することにより、どのように電気を生み出すのか理解しましょう。