私たちは車やバス、エレベーターなどの乗り物に乗ることが多いです。こうした乗り物は人を乗せて移動します。このとき、私たちが感じる力に慣性力があります。
乗り物が加速すると、私たちは逆向きで同じ加速度を受けます。つまり、乗り物が移動している向きとは反対方向に力が加わるのです。慣性力は私たちが日常的に経験している力であり、物理では慣性力を学びます。
乗り物の加速によって観測者に働く力であるため、慣性力は特殊です。ただ相対速度で考えれば、なぜ慣性力で負の加速度が働くのかわかります。
それではどのように慣性力を利用して式を作り、計算すればいいのでしょうか。慣性力の公式や計算式の作り方を解説していきます。
もくじ
乗り物が加速度\(a\)で移動すると、乗り物の中では\(-a\)の加速度が加わる
慣性力で重要になるのが乗り物です。乗り物が急発進したり、急停止したりすると、乗り物に乗っている人はよろめきます。
つまり、乗り物の急発進や急停止によって乗客に力が加わります。このとき乗客に加わる力が慣性力です。
重要なのは、観測者(乗客)が乗り物と共に動いているという事実です。乗り物と同じ加速度で観測者(乗客)の速度は上昇します。このような状況のとき、慣性力が働きます。具体的には、乗り物の加速度が\(a\)のとき、乗客に加わる加速度は\(-a\)です。言い換えると、反対向きに加速度\(a\)が加わります。
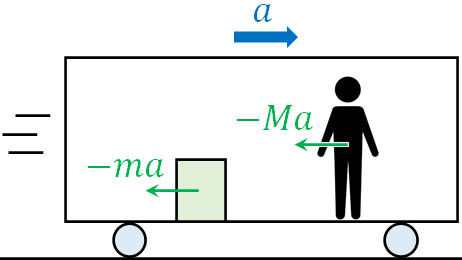
車が発進して加速していくとき、慣性力によってあなたには後ろ向きに力が加わります。一方で車が停止することで負の加速をしているとき、慣性力によってあなたは前向きに力が加わります。これら日常生活での経験を考えると、乗り物の向きと反対方向に力が加わる事実は納得できます。
慣性力とは、相対速度・相対加速度を意味する
それでは、なぜ慣性力は乗り物が加速する向きとは反対方向に加わるのでしょうか。相対速度・相対加速度で考えれば、この理由を理解できます。
物理で重要なのは相対速度です。例えばあなたが車を利用して50km/hで移動していても、ほかの車も49km/hで同方向に移動している場合、相対速度(速度の違い)は1km/hです。この場合、たとえ車同士が衝突しても損害は少ないです。これは相対速度が小さいからです。
相対速度では、仮に一方の物体を静止の状態と考えるとき、2つの物体の速度にどれだけの差があるのかを表します。先ほどの例では、一方の車を静止の状態と考えるとき、相対速度は1km/hというわけです。
それでは、あなたが乗り物の中にいるとき、相対速度はどのようになっているでしょうか。あなたは乗り物と一緒に動いています。そこで相対速度を考慮するため、仮にあなたが静止していると仮定しましょう。
あなたが乗り物に乗って移動しているとき、窓の景色はどのように見えるでしょうか。あなたがバスに乗り、窓から外を眺めると、景色は後ろへ流れていきます。つまりあなたを基準にすると(あなたが静止していると仮定すると)、外の世界は負の方向(後ろ向き)に動いています。

相対速度を利用し、あなたを基準にしてあなたが静止している場合、乗り物の外の世界は加速度\(-a\)によって時間経過と共に負の方向へ加速していることになります。
このように相対速度と相対加速度で考えれば、なぜ乗り物の中では逆方向に力が働くのかわかります。乗り物が速度\(v\)で走っている場合、乗客が窓から外を見ると\(-v\)の速度で外の世界が動いているように感じます。
同様に乗り物が加速度\(a\)にて速度を上げる場合、乗客を基準にすると\(-a\)の加速度にて外の世界が動くことになります。結果として、乗客には加速度\(-a\)による慣性力が働きます。
慣性力が働くときの運動
それでは、慣性力が働くときはどのように式を作ればいいのでしょうか。物理の計算ではベクトル(物体が進む向き)を考えなければいけません。
ただ物理で練習問題を解くとき、問題文を読んでも加速度の方向が不明なケースは多いです。その場合、実際にあなたが乗り物の中にいる場面を想像しましょう。そうすれば、加速度が加わる向きがわかります。
例えば、以下の問題の答えは何でしょうか。
- あなたはエレベーターに乗っており、天井に質量\(m\)の重りがつるされています。エレベーターが加速度\(a\)で上昇するとき、糸の張力\(T\)はいくらでしょうか。なお、重力加速度は\(g\)です。
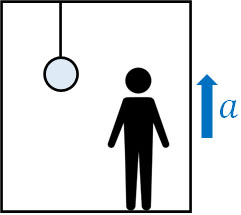
エレベーターが静止している場合、張力は\(T=mg\)です。ただエレベーターは上に移動しています。つまり慣性力による力を加えなければいけません。加速度は\(a\)であるため、慣性力は\(ma\)です。それでは、慣性力\(ma\)を張力\(T\)に対して足せばいいのでしょうか、それとも引けばいいのでしょうか。
あなたが実際にエレベーターに乗っているとき、エレベーターが速いスピードで上昇すると、あなたは下に押さえつけられます。そうした場面を想像することができれば、エレベーターが上昇するときは下向きに力が加わっているとわかります。
「エレベーターが加速度\(a\)で上昇しているため、そのた反対向きに慣性力が働く」と考えてもいいですが、応用問題になると慣性力の働く向きがわからず、多くの人が計算ミスをします。そこで実際に私たちに起こっている物理現象をイメージし、力が働く方向性を考えましょう。
なおエレベーターが上昇するとき、下向きに加速度\(a\)が加わるため、以下の図を作れます。
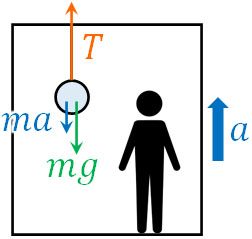
こうして、\(T=ma+mg\)とわかります。エレベーター内では、物体は静止しています。そこで、加速度\(a\)を考慮してつり合いの式を作りましょう。
乗り物の外から見る場合、運動方程式によって式を作れる
なお慣性力を利用しなくても、先ほどの式を作ることができます。エレベーターの中にあなたが立っている場合、重りは静止しているため、力のつり合いの式を作らなければいけません。一方でエレベーターの中ではなく、エレベーターの外にあなたが立っている場面を考えましょう。
この場合、物体(重り)は動いています。そこで、質量\(m\)の物体が加速度\(a\)で上昇するときの運動方程式を作りましょう。そうすると、重りが上昇するときの式は以下のようになります。
\(ma=T-mg\)
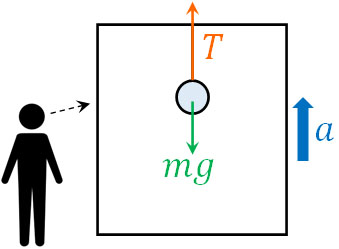
こうして、\(T=ma+mg\)と同じ式を作ることができました。加速度\(a\)は同じであるため、あなたがエレベーターの中にいても外にいても、当然ながら張力\(T\)は同じです。そのため、同じ式を作れるのです。
ただ式は同じであっても、式を作るときの考え方は異なります。そこであなたが実際に乗り物の中にいると仮定して、慣性力を用いた式を作れるようになりましょう。
糸を切るときの落下時間を求める練習問題
それでは、慣性力を用いる練習問題を解いてみましょう。以下の問題の答えは何でしょうか。
- 加速度\(a\)で下降するエレベーター内に質量\(m\)の重りがつるされています。エレベーターの床から重りまでの高さが\(h\)のとき、糸を切って床に落下するまでの時間を求めましょう。なお、重力加速度は\(g\)です。
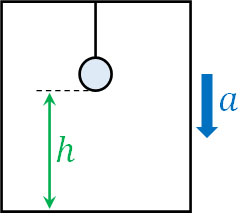
あなたがエレベーターの中にいて、仮にエレベーターが勢いよく下に落ちる場合、あなたは宙に浮きます。これは、あなたに対して上向きの力が加わるからです。上向きの力が働くからこそ、物体は宙に浮くのです。つまりエレベーターが加速度\(a\)で下降するというのは、エレベーター内では上向きに加速度\(a\)が加わります。
また、エレベーターが下に落ちているとき、エレベーターの床に到着するまでに時間がかかります。そのため、重りは通常よりも長い時間をかけて床に到着すると予想できます。
これらの内容を踏まえて式を作りましょう。エレベーターの中にあなたがいるとき、糸を切った後の重りの加速度\(a’\)を求めましょう。この場合、運動方程式は以下のようになります。
\(ma’=mg-ma\)
\(a’=g-a\)
エレベーターは下降しているため、あなたや物体にかかる力は小さくならなければいけません。このため、この式を作ることができます。
また通常よりも長い時間をかけて床に到着するため、加速度\(a’\)は重力加速度\(g\)よりも小さい値でなければいけません。そのため実際の物理現象を考えても、\(a’=g-a\)は正しい式であるとわかります。
なお重りが落ちるときの加速度がわかったため、等加速度直線運動の公式を利用して床までの到着時間を計算しましょう。\(x=v_0t+\displaystyle\frac{1}{2}at^2\)の公式に代入すると、以下のようになります。
\(h=0t+\displaystyle\frac{1}{2}(g-a)t^2\)
\(t^2=\displaystyle\frac{2h}{g-a}\)
\(t=\sqrt{\displaystyle\frac{2h}{g-a}}\) (\(t>0\))
こうして、床に到着するまでの時間は\(t=\sqrt{\displaystyle\frac{2h}{g-a}}\)とわかりました。
物体の落下と慣性力に関する練習問題
次に、応用力を必要とする練習問題を解きましょう。以下の問題の答えは何でしょうか。
- 地面との角度がθである斜面台が加速度\(a\)で左方向に動いています。斜面台に質量\(m\)の物体があり、物体が静止しているとき、加速度\(a\)を求めましょう。なお物体と斜面台に摩擦はなく、重力加速度は\(g\)です。
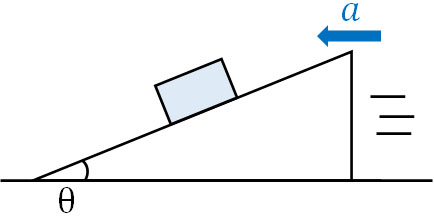
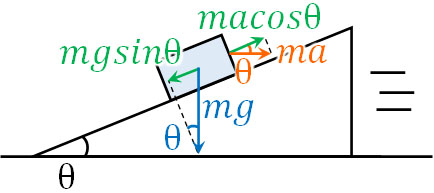
摩擦のない斜面に物体を置く場合、物体は下へ滑ります。しかし斜面台が動いている場合、慣性力によって物体は斜面の上を登ろうとする力が働きます。つまり物体が静止している状態では、重力による影響(物体が下に落ちる力)と慣性力(物体が上に登る力)が同じです。
そこで、以下の式を作りましょう。
\(mgsinθ=macosθ\)
\(a=\displaystyle\frac{gsinθ}{cosθ}\)
\(a=gtanθ\)
こうして、加速度\(a\)が\(gtanθ\)の場合、物体は斜面台で静止します。
物体に働く慣性力を計算する
加速している物体に乗っている場合、必ず進行方向とは逆向きの力が働きます。これが慣性力であり、私たちは日常的に慣性力を経験しています。
相対速度と相対加速度で考えると、なぜ慣性力が働くのか理解できます。乗り物に乗っているあなたを基準にすると、負の方向に加速度が働きます。そのため、進行方向とは逆向きに力が加わるのです。この性質を利用して式を作りましょう。
なお実際に式を作るとき、加速度の向きがわからないケースは多いです。そこで、実際に物理現象が起こっている場面を想像し、加速度が加わっている向きを判断しましょう。
物体が静止しているときは力のつり合いの式を作りましょう。また物体が移動している場合、運動方程式を利用して式を作りましょう。そうすれば、慣性力を用いる式を作れるようになります。






