位置ベクトルを利用することにより、点をベクトルで表すことができます。位置ベクトルはベクトルの一種であるため、ベクトルとしての性質を利用できます。
例えば2つのベクトルが直角の場合、内積はゼロになります。また角の二等分線であれば、内分点の公式とベクトルを利用することによって、向きとベクトルの大きさ(長さ)を表すことができます。
こうした性質を利用することにより、垂心・内心・外心の位置ベクトルに関する問題を解けるようになります。またベクトルでは証明問題が出されるため、ベクトルの性質を利用することによって証明できるようにならなければいけません。
それでは、どのように位置ベクトルを利用して垂心・内心・外心に関する問題を解けばいいのでしょうか。これらの問題の解き方や証明の方法を解説していきます。
もくじ
垂心では内積がゼロになる性質を利用する
垂心とは、三角形の頂点から辺に対して垂直に引いた線の交点を指します。そのため△OABについて、頂点から垂心Hに引く線と三角形の辺は必ず直角になります。
- \(OH⊥AB\)
- \(AH⊥OB\)
- \(BH⊥OA\)
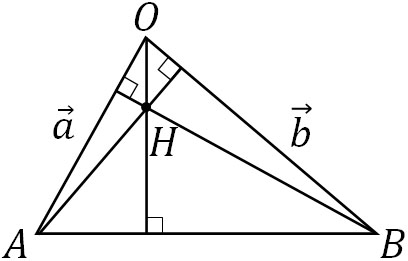
直角というのは、ベクトルの内積がゼロになることを意味します。また、もう一つ利用するべき性質があります。一つのベクトルを二つのベクトルに分解することができるのです。そこで、\(\overrightarrow{OH}\)を以下のように分解しましょう。
- \(\overrightarrow{OH}=s\overrightarrow{a}+t\overrightarrow{b}\)
\(s\)や\(t\)の値は不明です。ただ同じ平面上に存在するため、このようにベクトルを分解することが可能です。垂心の位置ベクトルでは、この性質を利用することで問題を解きましょう。それでは、以下の問題の答えは何でしょうか。
- △OABについて、\(OA(|\overrightarrow{a}|)=3\)、\(OB(|\overrightarrow{b}|)=2\)、\(∠AOB=60°\)です。△OABの垂心をHとするとき、\(\overrightarrow{a}\)と\(\overrightarrow{b}\)を用いて\(\overrightarrow{OH}\)を表しましょう。
図を描くと以下のようになります。
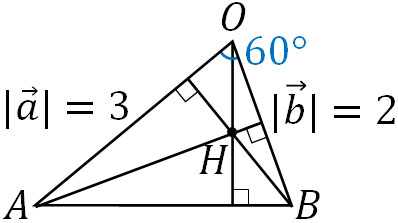
先ほど解説した通り、\(\overrightarrow{OH}=s\overrightarrow{a}+t\overrightarrow{b}\)と表すことができます。また\(OH⊥AB\)であるため、以下のように計算しましょう。
\(\overrightarrow{OH}·\overrightarrow{AB}=0\)
\((s\overrightarrow{a}+t\overrightarrow{b})(\overrightarrow{OB}-\overrightarrow{OA})=0\)
\((s\overrightarrow{a}+t\overrightarrow{b})(\overrightarrow{b}-\overrightarrow{a})=0\)
\(-s|\overrightarrow{a}|^2+t|\overrightarrow{b}|^2+(s-t)\overrightarrow{a}·\overrightarrow{b}=0\)
\(-9s+4t+(s-t)\overrightarrow{a}·\overrightarrow{b}=0\)
なお\(∠AOB=60°\)であるため、内積を利用して以下のように計算できます。
\(\overrightarrow{a}·\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cos60°\)
\(\overrightarrow{a}·\overrightarrow{b}=3×2×\displaystyle\frac{1}{2}\)
\(\overrightarrow{a}·\overrightarrow{b}=3\)
そのため、\(\overrightarrow{a}·\overrightarrow{b}=3\)を先ほどの式に代入しましょう。
\(-9s+4t+(s-t)\overrightarrow{a}·\overrightarrow{b}=0\)
\(-9s+4t+3(s-t)=0\)
\(-6s+t=0\)
\(t=6s\)
次に、\(AH⊥OB\)を利用して式を作りましょう。
\(\overrightarrow{AH}·\overrightarrow{OB}=0\)
\((\overrightarrow{OH}-\overrightarrow{OA})\overrightarrow{b}=0\)
\((\overrightarrow{OH}-\overrightarrow{a})\overrightarrow{b}=0\)
\(\overrightarrow{OH}·\overrightarrow{b}-\overrightarrow{a}·\overrightarrow{b}=0\)
\((s\overrightarrow{a}+t\overrightarrow{b})\overrightarrow{b}-3=0\)
\(s\overrightarrow{a}·\overrightarrow{b}+t|\overrightarrow{b}|^2-3=0\)
\(3s+4t=3\)
\(t=6s\)であるため、式に代入しましょう。
\(3s+24s=3\)
\(27s=3\)
\(s=\displaystyle\frac{1}{9}\)
\(s=\displaystyle\frac{1}{9}\)であるため、\(t=\displaystyle\frac{2}{3}\)です。こうして、\(\overrightarrow{OH}=\displaystyle\frac{1}{9}\overrightarrow{a}+\displaystyle\frac{2}{3}\overrightarrow{b}\)とわかりました。
内心の位置ベクトルでは角の二等分線の定理を使う
次に、内心の位置ベクトルに関する問題の解き方を学びましょう。三角形に存在する三つの角について、角の二等分線の交点を内心といいます。内心は三角形の内接円の中心でもあります。
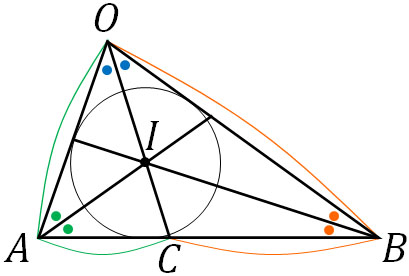
この定義を理解すれば、内心の位置ベクトルに関する問題を解くことができます。角の二等分線の定理より、上図で\(OA:OB=AC:BC\)です。点Cは線分ABの内分点であるため、OAとOBの長さがわかれば、\(\overrightarrow{OA}\)と\(\overrightarrow{OB}\)を利用して\(\overrightarrow{OC}\)を表すことができます。
さらに、\(∠OAB\)の二等分線に着目することにより、\(\overrightarrow{OI}\)を表すことができます。これが、内心の位置ベクトルに関する問題を解くときの考え方です。それでは、以下の問題を解いてみましょう。
- △OABについて、\(OA(|\overrightarrow{a}|)=5\)、\(OB(|\overrightarrow{b}|)=6\)、\(AB=7\)です。△OABの内心をIとするとき、\(\overrightarrow{a}\)と\(\overrightarrow{b}\)を用いて\(\overrightarrow{OI}\)を表しましょう。
図を作ると以下のようになります。
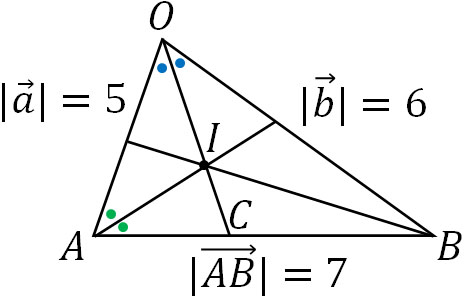
角の二等分線の定理より、以下の関係が成り立ちます。
- \(OA:OB=AC:BC=5:6\)
そのため内分点の公式を利用すると、以下のように\(\overrightarrow{OC}\)を表すことができます。
- \(\overrightarrow{OC}=\displaystyle\frac{6\overrightarrow{a}+5\overrightarrow{b}}{5+6}=\displaystyle\frac{6\overrightarrow{a}+5\overrightarrow{b}}{11}\)
次にACの長さを計算しましょう。\(AC:BC=5:6\)であるため、ACの長さは\(\displaystyle\frac{35}{11}\)です。
\(7×\displaystyle\frac{5}{11}=\displaystyle\frac{35}{11}\)
そこで\(∠OAB\)の二等分線に着目しましょう。点Iは線分OCの内分点であるため、\(AO:AC=OI:CI\)になります。つまり、OIの長さを得ることができます。以下のように計算しましょう。
\(AO:AC=OI:CI=5:\displaystyle\frac{35}{11}\)
\(OI:CI=11:7\)
\(OI:CI=11:7\)であるため、\(OI=\displaystyle\frac{11}{18}\overrightarrow{OC}\)です。\(\overrightarrow{OC}=\displaystyle\frac{6\overrightarrow{a}+5\overrightarrow{b}}{11}\)であるため、以下のように計算しましょう。
\(\overrightarrow{OI}=\displaystyle\frac{11}{18}\overrightarrow{OC}\)
\(\overrightarrow{OI}=\displaystyle\frac{11}{18}×\displaystyle\frac{6\overrightarrow{a}+5\overrightarrow{b}}{11}\)
\(\overrightarrow{OI}=\displaystyle\frac{6\overrightarrow{a}+5\overrightarrow{b}}{18}\)
こうして、\(\overrightarrow{a}\)と\(\overrightarrow{b}\)を用いて\(\overrightarrow{OI}\)を表すことができました。
外心の位置ベクトルでは内積を利用する
それでは、外心の位置ベクトルはどのように考えればいいのでしょうか。三角形に存在する3つの辺について、それぞれの辺の垂直二等分線の交点を外心といいます。また外心というのは、三角形の外接円の中心でもあります。
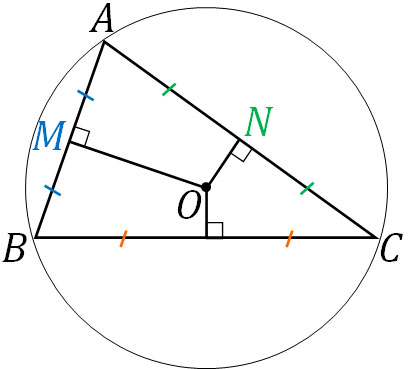
そこでABとACの中点をそれぞれ点M、点Nとすると、上図では以下の関係が成り立ちます。
- \(AB⊥MO\)
- \(AC⊥NO\)
つまり、ベクトルの内積がゼロになります。外心の位置ベクトルでは、この性質を利用して問題を解きましょう。なお外心では、円の性質を利用することにより、\(OA=OB=OC\)となります。この性質を利用することにより、問題を解くケースもあります。
それでは、以下の問題の答えは何でしょうか。
- △ABCについて、\(AB=5\)、\(BC=7\)、\(CA=8\)、三角形の外心を点Oとします。\(\overrightarrow{AB}\)と\(\overrightarrow{AC}\)を利用して、\(\overrightarrow{AO}\)を表しましょう。
AMとACの中点をそれぞれ点M、点Nとすると、図は以下のようになります。
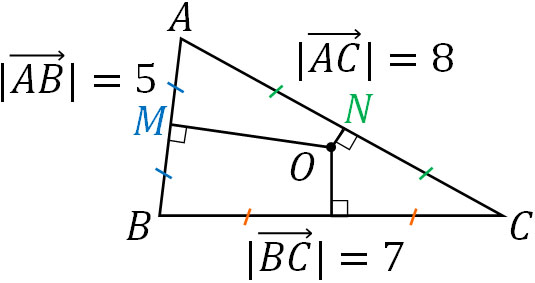
余弦定理より、\(cosA\)を計算しましょう。
\(7^2=5^2+8^2-2×5×8×cosA\)
\(-cosA=-\displaystyle\frac{49-25-64}{80}\)
\(cosA=\displaystyle\frac{1}{2}\)
cosAがわかったため、以下のように内積を計算しましょう。
\(\overrightarrow{AB}·\overrightarrow{AC}=|\overrightarrow{AB}||\overrightarrow{AC}|cosA\)
\(\overrightarrow{AB}·\overrightarrow{AC}=5×8×\displaystyle\frac{1}{2}\)
\(\overrightarrow{AB}·\overrightarrow{AC}=20\)
ここで、\(\overrightarrow{AO}=s\overrightarrow{AB}+t\overrightarrow{AC}\)とします。また\(\overrightarrow{AB}·\overrightarrow{MO}=0\)であり、\(\overrightarrow{AC}·\overrightarrow{NO}=0\)であるため、内積がゼロである性質を利用して2つの式を作りましょう。
・\(\overrightarrow{AB}·\overrightarrow{MO}=0\)より
\(\overrightarrow{AB}·\overrightarrow{MO}=0\)
\(\overrightarrow{AB}(\overrightarrow{AO}-\overrightarrow{AM})=0\)
\(\overrightarrow{AB}(\overrightarrow{AO}-\displaystyle\frac{1}{2}\overrightarrow{AB})=0\)
\(-\displaystyle\frac{1}{2}|\overrightarrow{AB}|^2+\overrightarrow{AB}·\overrightarrow{AO}=0\)
\(\overrightarrow{AB}(s\overrightarrow{AB}+t\overrightarrow{AC})=\displaystyle\frac{25}{2}\)
\(s|\overrightarrow{AB}|^2+t\overrightarrow{AB}·\overrightarrow{AC}=\displaystyle\frac{25}{2}\)
\(25s+20t=\displaystyle\frac{25}{2}\)
\(10s+8t=5\) – ①
・\(\overrightarrow{AC}·\overrightarrow{NO}=0\)より
\(\overrightarrow{AC}·\overrightarrow{NO}=0\)
\(\overrightarrow{AC}(\overrightarrow{AO}-\overrightarrow{AN})=0\)
\(\overrightarrow{AC}(\overrightarrow{AO}-\displaystyle\frac{1}{2}\overrightarrow{AC})=0\)
\(-\displaystyle\frac{1}{2}|\overrightarrow{AC}|^2+\overrightarrow{AC}·\overrightarrow{AO}=0\)
\(-32+\overrightarrow{AC}(s\overrightarrow{AB}+t\overrightarrow{AC})=0\)
\(s\overrightarrow{AB}·\overrightarrow{AC}+t|\overrightarrow{AC}|^2=32\)
\(20s+64t=32\)
\(5s+16t=8\) – ②
\(①-②×2\)をすると、以下のように計算できます。
\(-24t=-11\)
\(t=\displaystyle\frac{11}{24}\)
\(t=\displaystyle\frac{11}{24}\)であるため、以下のように\(s\)を計算できます。
\(10s+8×\displaystyle\frac{11}{24}=5\)
\(10s+\displaystyle\frac{11}{3}=5\)
\(30s+11=15\)
\(s=\displaystyle\frac{4}{30}\)
\(s=\displaystyle\frac{2}{15}\)
こうして、\(\overrightarrow{AO}=\displaystyle\frac{2}{15}\overrightarrow{AB}+\displaystyle\frac{11}{24}\overrightarrow{AC}\)とわかりました。
ベクトルが関わる証明問題を解く
三角形の性質を利用することで証明問題を解かなければいけないことは多いです。そこで、ここまで解説した知識を利用することにより、ベクトルを用いて証明できるようになりましょう。二乗したり、内積を利用したりして証明するのです。
それでは、以下の証明問題を解いてみましょう。
- △ABCで外接円の中心をOとします。\(\overrightarrow{OH}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\)となる点Hについて、点Hは△ABCの垂心であることを証明しましょう。
ベクトルでは図を描かないと問題を解くのが難しいです。そこで、以下のように図を描きましょう。
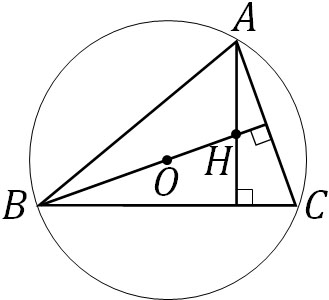
点Hが垂心である場合、以下の関係が成り立ちます。
- \(AH⊥BC\):\(\overrightarrow{AH}·\overrightarrow{BC}=0\)
- \(BH⊥AC\):\(\overrightarrow{BH}·\overrightarrow{AC}=0\)
また点Oは外心であるため、\(OA=OB=OC\)となります。これらの性質を利用して証明問題を解きましょう。
\(\overrightarrow{OH}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\)
\(\overrightarrow{AH}-\overrightarrow{AO}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\)
\(\overrightarrow{AH}+\overrightarrow{OA}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\)
\(\overrightarrow{AH}=\overrightarrow{OB}+\overrightarrow{OC}\)
そこで、\(\overrightarrow{AH}·\overrightarrow{BC}\)を計算します。
\(\overrightarrow{AH}·\overrightarrow{BC}\)
\(=(\overrightarrow{OB}+\overrightarrow{OC})(\overrightarrow{OC}-\overrightarrow{OB})\)
\(=|\overrightarrow{OC}|^2-|\overrightarrow{OB}|^2\)
\(=0\)
\(OA=OB=OC\)であるため、\(|\overrightarrow{OB}|^2-|\overrightarrow{OC}|^2=0\)になります。同様の方法で\(\overrightarrow{BH}·\overrightarrow{AC}=0\)を確認しましょう。
\(\overrightarrow{OH}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\)
\(\overrightarrow{BH}-\overrightarrow{BO}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\)
\(\overrightarrow{BH}+\overrightarrow{OB}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\)
\(\overrightarrow{BH}=\overrightarrow{OA}+\overrightarrow{OC}\)
そこで、\(\overrightarrow{BH}·\overrightarrow{AC}\)を計算します。
\(\overrightarrow{BH}·\overrightarrow{AC}\)
\(=(\overrightarrow{OA}+\overrightarrow{OC})(\overrightarrow{OC}-\overrightarrow{OA})\)
\(=|\overrightarrow{OC}|^2-|\overrightarrow{OA}|^2\)
\(=0\)
\(\overrightarrow{AH}≠0\)、\(\overrightarrow{BC}≠0\)、\(\overrightarrow{BH}≠0\)、\(\overrightarrow{AC}≠0\)であるため、\(AH⊥BC\)、\(BH⊥AC\)です。そのため、点Hは△ABCの垂心です。
垂心・内心・外心の性質と位置ベクトルを利用する
ベクトルを利用するとき、三角形の性質を学ぶことは重要です。特に垂心・内心・外心については、それぞれ何を意味しているのか知っていないと問題を解くことができません。
そこで、それぞれの定義を学びましょう。また、どのような性質があるのか覚えましょう。ベクトルの性質に加えて、垂心・内心・外心の性質を利用することによって答えを得られるようになります。そこで、ベクトルの内積や垂直二等分線の定理を利用できるようになりましょう。
また、垂心・内心・外心の性質を利用して証明問題を解かなければいけないこともあります。それぞれの性質を覚えていないと、当然ながら証明することはできません。
図形が関わる問題で三角形はひんぱんに利用されます。そこで三角形の性質を復習し、ベクトルに関わる問題を解けるようになりましょう。