平面の方程式と空間の直線の方程式：ベクトル方程式

私たちは線や面の計算方法を数学で学びます。ただ、これらは平面での計算です。それでは、空間座標で線や面の計算をするにはどうすればいいのでしょうか。

立体図形の計算では、空間ベクトルを利用できます。空間ベクトルを利用することにより、立体座標での平面の方程式と直線の方程式を得ることができます。

また方程式を利用して平面や空間の直線を表現できるだけでなく、応用問題を解けるようにならなければいけません。球面と平面の交点を計算したり、平面と直線によるなす角を得たりするのです。これらの計算には、平面の方程式と直線の方程式の両方を利用することになります。

それでは、空間ベクトルを利用してどのように方程式を導出すればいいのでしょうか。平面の方程式と空間の直線の方程式について、使い方を解説していきます。

1 空間座標での平面の方程式と公式
- 1.1 平面のベクトル方程式を法線ベクトルで表す
- 1.2 3つのベクトルを用いるベクトル方程式
2 空間の直線のベクトル方程式
- 2.1 一つの点を通る空間の直線の方程式
- 2.2 二つの点を通る空間の直線の方程式
3 直線と平面のなす角：法線ベクトルの利用
- 3.1 球面と平面によって作られる円の方程式
4 空間図形での平面と直線の方程式を利用する

空間座標での平面の方程式と公式

まず、平面の方程式を確認しましょう。\(ax+by+c=0\)により、二次元での直線を表せることはすでに知っていると思います。ただ空間座標での平面は二次元ではなく三次元であるため、\(z\)軸を加える必要があります。

そのため、空間座標での平面の方程式は以下のようになります。

\(ax+by+cz+d=0\)

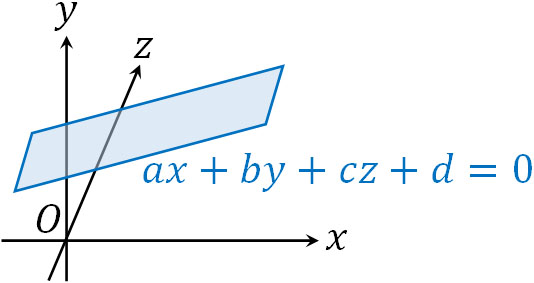
このように二次元での直線の方程式に対して、\(z\)軸の要素を加えることで平面の方程式となります。

平面のベクトル方程式を法線ベクトルで表す

それでは、空間座標で平面の方程式をどのように導出するのでしょうか。平面の方程式を得るとき、空間ベクトルが便利です。そこで、まずは平面のベクトル方程式を学びましょう。

三次元空間に存在する平面について、法線ベクトル\(\overrightarrow{n}\)を用いて表せます。特定のベクトルに対して、垂直なベクトルが法線ベクトルです。なぜ法線ベクトルを利用するかというと、平面では特定の法線ベクトルに対してすべての位置で垂直だからです。

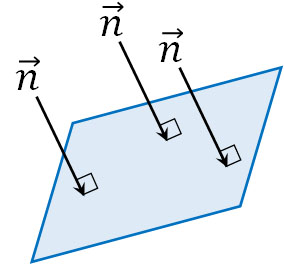
そこで平面上に存在する点Aと点Pに対して、垂直な法線ベクトル\(\overrightarrow{n}\)を考えましょう。点Aと点Pが平面上のどこに存在していたとしても、法線ベクトル\(\overrightarrow{n}\)に垂直なので以下の関係が成り立ちます。

\(\overrightarrow{AP}·\overrightarrow{n}=0\)

\((\overrightarrow{p}-\overrightarrow{a})·\overrightarrow{n}=0\)

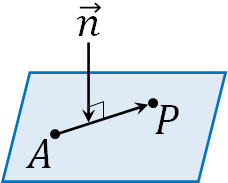
こうして、平面のベクトル方程式を得ることができました。

それでは定点Aを\(\overrightarrow{a}=(x_1,y_1,z_1)\)、平面上の任意の点Pを\(\overrightarrow{p}=(x,y,z)\)、法線ベクトルを\(\overrightarrow{n}=(a,b,c)\)とします。この場合、先ほどのベクトル方程式より以下の式を作ることができます。

\((x-x_1)a+(y-y_1)b+(z-z_1)c\)\(=0\)

\(ax+by+cz-(ax_1+by_1+cz_1)\)\(=0\)

Aは定点であるため、座標は明確にわかります。また、法線ベクトルもわかっています。そのため、\(ax_1+by_1+cz_1\)は定数です。そこで\(ax_1+by_1+cz_1=-d\)としましょう。これにより、先ほど記した平面の方程式を得ることができます。

\(ax+by+cz+d=0\)

それでは、以下の問題を解いてみましょう。

ベクトル方程式を用いて、A\((1,1,-1)\)、B\((0,2,3)\)、C\((-1,0,4)\)を通る平面の方程式を求めましょう。

\(ax+by+cz+d=0\)へ代入し、連立方程式を解くことによって答えを得ることができます。そこで、以下の式を作りましょう。

\(a+b-c+d=0\) – ①
\(2b+3c+d=0\) – ②
\(-a+4c+d=0\) – ③

・\(①-②\)より

\(a-b-4c=0\) – ④

・\(②-③\)より

\(a+2b-c=0\) – ⑤

・\(④-⑤×4\)より

\(-3a-9b=0\)

\(b=-\displaystyle\frac{1}{3}a\)

・\(④×2+⑤\)より

\(3a-9c=0\)

\(c=\displaystyle\frac{1}{3}a\)

それでは、①へ\(b=-\displaystyle\frac{1}{3}a\)と\(c=\displaystyle\frac{1}{3}a\)を代入しましょう。

\(a+b-c+d=0\)

\(a-\displaystyle\frac{1}{3}a-\displaystyle\frac{1}{3}a+d=0\)

\(\displaystyle\frac{1}{3}a+d=0\)

\(d=-\displaystyle\frac{1}{3}a\)

そのため、平面の方程式へ\(b=-\displaystyle\frac{1}{3}a\)、\(c=\displaystyle\frac{1}{3}a\)、\(d=-\displaystyle\frac{1}{3}a\)を代入すると以下の式を作れます。

\(ax-\displaystyle\frac{1}{3}ay+\displaystyle\frac{1}{3}az-\displaystyle\frac{1}{3}a\)\(=0\)

\(3ax-ay+az-a=0\)

\(a≠0\)であるため、両辺を\(a\)で割りましょう。

\(3x-y+z-1=0\)

こうして、平面の方程式を得ることができました。

3つのベクトルを用いるベクトル方程式

なお空間座標の平面を決めるとき、法線ベクトルを利用しない方法もあります。2つの点（点Aと点B）を通る空間の平面では、特定の平面を指定できません。辺ABを軸に回転できるからです。

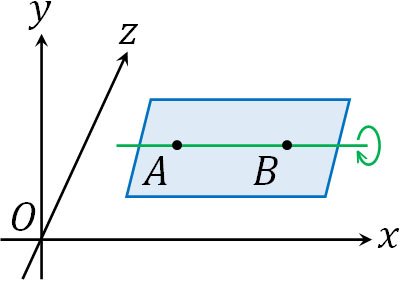
そのため法線ベクトルを利用しない場合、ABに加えて点Cを利用しましょう。立体では、3つの点を通る場合、一つの平面を特定できます。

また空間ベクトルでは、「共面条件を利用することにより、A、B、Cの3点を通る平面上の点Pを表せる」ことをすでに学んでいると思います。つまり、空間ベクトルでの共面条件というのは、立体座標での平面のベクトル方程式でもあるのです。

そこで点A（\(\overrightarrow{a}\)）、点B（\(\overrightarrow{b}\)）、点C（\(\overrightarrow{c}\)）を通る平面について、平面上にある任意の点をP（\(\overrightarrow{p}\)）とするとき、以下のベクトル方程式が成り立ちます。

\(\overrightarrow{p}=s\overrightarrow{a}+t\overrightarrow{b}+u\overrightarrow{c}\)
\(s+t+u=1\)

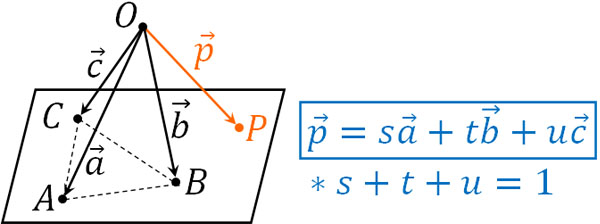
空間ベクトルでの共面条件と立体座標での平面のベクトル方程式が同じであることを学べば、ベクトルが何を意味しているのかより理解できます。

空間の直線のベクトル方程式

次に、空間の直線のベクトル方程式を学びましょう。空間の直線のベクトル方程式は、平面ベクトルでの直線のベクトル方程式と公式が同じです。定点A（\(\overrightarrow{a}\)）を通り、特定の方向をもつベクトル\(\overrightarrow{d}\)に平行な点P（\(\overrightarrow{p}\)）は以下のように表すことができます。

\(\overrightarrow{p}=\overrightarrow{a}+t\overrightarrow{d}\)

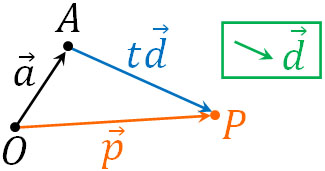
\(t\)は実数であり、さまざまな値になることができます。そのため点Pがつながることによって直線になります。

また異なる2点（AとB）を通る空間の直線については、位置ベクトルを利用することで以下のように表せます。

\(\overrightarrow{p}=(1-t)\overrightarrow{a}+t\overrightarrow{b}\)

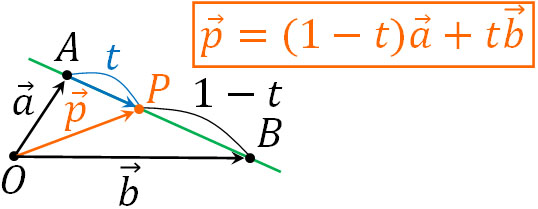
2点を通る必要があるため、ベクトルの係数を足すと必ず1になります。この公式についても、平面ベクトルでの直線の方程式と同じです。平面ベクトルであっても空間ベクトルであっても、直線のベクトル方程式は変わりません。

一つの点を通る空間の直線の方程式

それでは、先ほどの知識を利用して立体座標での直線の方程式を導出しましょう。ベクトル方程式では公式が同じであるものの、立体座標では\(z\)軸が加わるため、平面座標と立体座標では直線の方程式が異なります。

そこで、定点Aを\(\overrightarrow{a}=(x_1,y_1,z_1)\)、直線上の任意の点Pを\(\overrightarrow{p}=(x,y,z)\)、\(\overrightarrow{d}=(l,m,n)\)とします。そうすると\(\overrightarrow{p}=\overrightarrow{a}+t\overrightarrow{d}\)であるため、以下の式を作れます。

\((x,y,z)=(x_1+tl,y_1+tm,z_1+tn)\)

こうして\(x=x_1+tl\)、\(y=y_1+tm\)、\(z=z_1+tn\)とわかります。そこで\(t\)の式にそろえるため、以下のように式を変形しましょう。

\(t=\displaystyle\frac{x-x_1}{l}\)
\(t=\displaystyle\frac{y-y_1}{m}\)
\(t=\displaystyle\frac{z-z_1}{n}\)

同じベクトルでは、当然ながら\(t\)の値が同じであるため、以下の関係が成り立ちます。

\(\displaystyle\frac{x-x_1}{l}=\displaystyle\frac{y-y_1}{m}=\displaystyle\frac{z-z_1}{n}\)

これが空間での直線の方程式です。ベクトル方程式を利用することにより、直線の方程式を導出できるのです。

二つの点を通る空間の直線の方程式

一方、二つの点を通る場合では、空間の直線の方程式をどのように計算すればいいのでしょうか。点Aを\(\overrightarrow{a}=(x_1,y_1,z_1)\)、点Bを\(\overrightarrow{a}=(x_2,y_2,z_2)\)とします。

このとき先ほどの\(\overrightarrow{d}\)について、\(\overrightarrow{d}=\overrightarrow{AB}\)と考えることができます。また、\(\overrightarrow{AB}=(x_2-x_1,y_2-y_1,z_2-z_1)\)です。\(\overrightarrow{d}=(l,m,n)\)なので、以下の関係が成り立ちます。

\(l=x_2-x_1\)
\(m=y_2-y_1\)
\(n=z_2-z_1\)

そこで\(l=x_2-x_1\)、\(m=y_2-y_1\)、\(n=z_2-z_1\)を\(\displaystyle\frac{x-x_1}{l}\)\(=\displaystyle\frac{y-y_1}{m}\)\(=\displaystyle\frac{z-z_1}{n}\)に代入しましょう。

\(\displaystyle\frac{x-x_1}{x_2-x_1}=\displaystyle\frac{y-y_1}{y_2-y_1}=\displaystyle\frac{z-z_1}{z_2-z_1}\)

こうして、2点を通る空間の直線の方程式を得ることができました。

直線と平面のなす角：法線ベクトルの利用

それでは、ここまで解説した内容を利用して応用問題を解けるようになりましょう。以下の問題の答えは何でしょうか。

平面\(x-4y+z=0\)と直線\(\displaystyle\frac{x-2}{4}\)\(=\displaystyle\frac{y+1}{-1}\)\(=z-3\)によって作られるなす角を求めましょう。

直線\(\displaystyle\frac{x-2}{4}\)\(=\displaystyle\frac{y+1}{-1}\)\(=z-3\)というのは、定点\((2,-1,3)\)を通り、\(\overrightarrow{d}=(4.-1,1)\)に平行な直線を指します。

なお空間座標で平面と直線の角度を計算するとき、法線ベクトルを利用しましょう。平面に対して、必ず垂直になるのが法線ベクトルです。法線ベクトルと直線の角度がわかれば、平面と直線の角度がわかるのです。

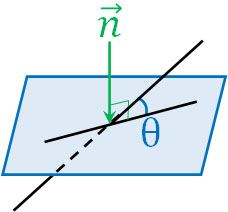
平面\(ax+by+cz+d=0\)について、\(\overrightarrow{n}=(a,b,c)\)は必ず法線ベクトルになります。つまり、\(x-4y+z=0\)の法線ベクトルは\(\overrightarrow{n}=(1,-4,1)\)です。方程式と法線ベクトルの関係は覚えましょう。

それでは、\(\overrightarrow{d}=(4.-1,1)\)と法線ベクトル\(\overrightarrow{n}=(1,-4,1)\)によって作られるなす角はいくらでしょうか。ベクトルの内積を利用することにより、角度を計算しましょう。まず、ベクトルの長さは以下のようになります。

\(|\overrightarrow{d}|=\sqrt{4^2+(-1)^2+1^2)}\)\(=3\sqrt{2}\)
\(|\overrightarrow{n}|=\sqrt{1^2+(-4)^2+1^2)}\)\(=3\sqrt{2}\)

また、内積は以下のようになります。

\(\overrightarrow{d}·\overrightarrow{n}\)

\(=4×1+(-1)×-4+1×1\)

\(=9\)

そこで、以下のように角度を計算します。

\(\overrightarrow{d}·\overrightarrow{n}=|\overrightarrow{d}||\overrightarrow{n}|cosθ\)

\(9=3\sqrt{2}×3\sqrt{2}×cosθ\)

\(cosθ=\displaystyle\frac{1}{2}\)

こうして、\(θ=60°\)とわかります。

ただ、\(\overrightarrow{d}\)と\(\overrightarrow{n}\)のなす角が60°です。そのため、直線と平面のなす角は\(90-60=30°\)です。

球面と平面によって作られる円の方程式

それでは、もう一つ問題を解きましょう。球面と平面が交わるとき、交点によって作られる円の方程式を得るのです。それでは、以下の問題の答えは何でしょうか。

中心Cが\((-1,2,3)\)であり、半径が6の球について、平面\(x-2y-4z-4=0\)との交点によって作られる円の中心Hの座標と半径を求めましょう。

中心Cが\((-1,2,3)\)であり、半径が6の球であるため、球面の方程式は以下になります。

\((x+1)^2+(y-2)^2+(z-3)^2=36\)

また、球の中心から平面に対して垂直に線を下ろすとき、交点をHとします。交点Hは球面と平面の交点によって作られる円の中心でもあります。

平面\(x-2y-4z-4=0\)に対して垂直な法線ベクトルは\(\overrightarrow{n}=(1,-2,-4)\)です。そのため球の中心\((-1,2,3)\)を通り、\(\overrightarrow{n}=(1,-2,-4)\)に平行な直線（辺CH）は以下のように表すことができます。