位置ベクトル：内分点・外分点・重心と共線条件・共点条件

平面ベクトルで学ぶ内容に位置ベクトルがあります。原点を基準にベクトルを考えることにより、計算するのです。

位置ベクトルの概念は座標とほぼ同じです。位置ベクトルでは原点を始点とするため、座標と同様に考えることで計算できます。図形では内分点や外分点、重心なども学びます。そのため位置ベクトルについても、内分点や外分点、重心の計算が可能です。また、利用する公式はほぼ同じです。

なお同じ直線上に存在することを証明したり、一つの点で交わることを示したりするときも位置ベクトルを利用できます。

それでは、どのように考えて位置ベクトルを利用し、計算問題を解けばいいのでしょうか。位置ベクトルの概念や計算方法、公式の使い方を解説していきます。

1 原点を始点とするベクトルが位置ベクトル
- 1.1 位置ベクトルによる内分点と外分点
- 1.2 三角形の重心の位置ベクトル
2 ベクトルを用いる共線条件
- 2.1 位置ベクトルが等しいと共点となる：共点条件
3 位置ベクトルを利用し、内分点や外分点を計算する

原点を始点とするベクトルが位置ベクトル

例えば\(\overrightarrow{AB}\)というのは、点Aから点Bを結ぶときの大きさ（長さ）と向きを表します。一方で原点Oを始点とするベクトルを位置ベクトルといいます。

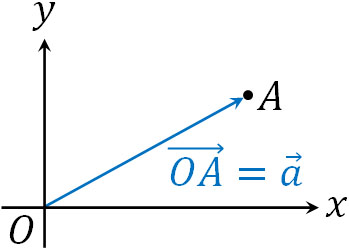
点Aがある場合、点Aの位置ベクトルは\(\overrightarrow{OA}\)を指します。このときOを省き、\(\overrightarrow{a}\)と位置ベクトルを記すこともひんぱんにあります。

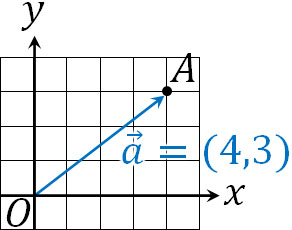
位置ベクトルというのは、要は座標と概念がほぼ同じです。例えば点A\((4,3)\)がある場合、\(\overrightarrow{OA}=\overrightarrow{a}=(4,3)\)となります。位置ベクトルが便利なのは、座標の計算と同じように扱えるからです。

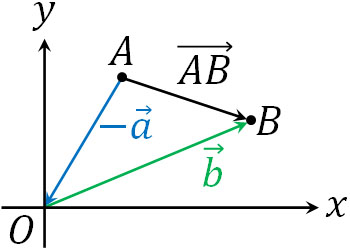
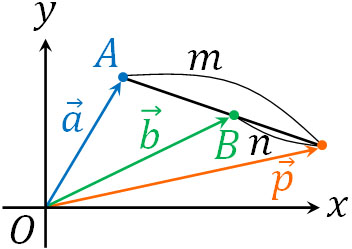
なお位置ベクトルを利用すれば、2つの点をつなぐベクトルについても表現できます。例えば、\(\overrightarrow{AB}=\overrightarrow{b}-\overrightarrow{a}\)です。以下のように図を作ると、\(\overrightarrow{a}\)の逆ベクトルと\(\overrightarrow{b}\)をつなぐことにより、\(\overrightarrow{AB}\)になるとわかります。

\(\overrightarrow{AB}=\overrightarrow{O\color{red}{B}}-\overrightarrow{O\color{red}{A}}=\overrightarrow{b}-\overrightarrow{a}\)

数学で計算をするとき、後から前を引くことで結果を得られます。ベクトルでも同様であり、後ろの位置ベクトルから前の位置ベクトルを引くことで表現しましょう。

位置ベクトルによる内分点と外分点

位置ベクトルを図形での座標と同様に扱えることを理解すれば、位置ベクトルであっても図形で利用される性質を利用できるとわかります。以下が図形の計算で利用される内分点の公式です。

\(x=\displaystyle\frac{na+mb}{m+n}\)

ベクトルを利用する内分点の公式はこれと同じであり、点Aの位置ベクトル\(\overrightarrow{a}\)と点Bの位置ベクトル\(\overrightarrow{b}\)について、線分ABを\(m:n\)に内分する位置ベクトル\(\overrightarrow{p}\)は以下のように表されます。

\(\overrightarrow{p}=\displaystyle\frac{n\overrightarrow{a}+m\overrightarrow{b}}{m+n}\)

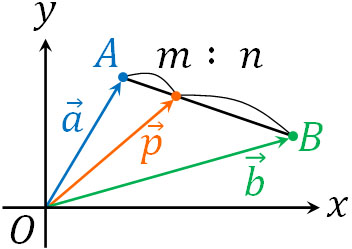
このように、内分点の公式はほぼ同じです。公式が同じ理由は単純であり、先ほど解説した通り、位置ベクトルは原点Oを始点とするからです。座標についても、原点Oを基準に考えます。そのため、座標利用でもベクトル利用でも内分点の公式はほぼ同じです。

なお内分点の公式がほぼ同じなのであれば、外分点の公式もほぼ同じです。位置ベクトルを利用するとき、外分点の公式は以下になります。

\(\overrightarrow{p}=\displaystyle\frac{-n\overrightarrow{a}+m\overrightarrow{b}}{m-n}\)

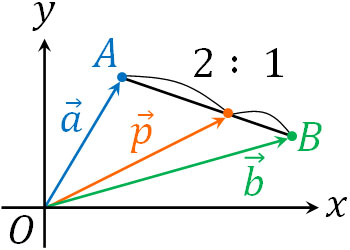
それでは、以下の問題の答えは何でしょうか。

点A（\(\overrightarrow{a}\)）と点B（\(\overrightarrow{b}\)）を結ぶ線分ABを\(2:1\)で内分する位置ベクトル\(\overrightarrow{p}\)を表しましょう。

先ほどの公式を利用すると、以下のように\(\overrightarrow{p}\)を表すことができます。

\(\overrightarrow{p}=\displaystyle\frac{\overrightarrow{a}+2\overrightarrow{b}}{3}\)

このように、公式を利用することで内分点を得られます。また、考え方は外分点も同じです。図形の問題で内分点と外分点の計算ができる場合、容易に理解できると思います。

三角形の重心の位置ベクトル

図形で内分点と外分点の公式を学ぶとき、同時に三角形の重心を得る公式も学びます。そこで、位置ベクトルを用いて重心を得る公式も覚えましょう。以下が位置ベクトルを用いて三角形の重心を得る公式です。

\(\displaystyle\frac{\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}}{3}\)

前述のとおり、位置ベクトルの考え方は座標と同じです。重心を得るとき、図形では\(x\)座標と\(y\)座標に分けて計算します。ベクトルには\(x\)成分と\(y\)成分が含まれているため、上記の公式になります。

なお、ベクトル成分を利用するときは\(x\)成分と\(y\)成分に分けて計算しましょう。それでは、以下の問題の答えは何でしょうか。

A:\(\overrightarrow{a}=(1,1)\)、B:\(\overrightarrow{b}=(-3,-4)\)、C:\(\overrightarrow{c}=(5,7)\)について、△ABCの重心の位置ベクトルG:\(\overrightarrow{g}\)を求めましょう。

公式を利用して計算すると以下のようになります。

\(x\)成分：\(\displaystyle\frac{1-3+5}{3}=1\)
\(y\)成分：\(\displaystyle\frac{1-4+7}{3}=\displaystyle\frac{4}{3}\)

こうして、三角形の重心の位置ベクトル\(\overrightarrow{g}=\left(1,\displaystyle\frac{4}{3}\right)\)を得ることができました。次に、証明問題を解いてみましょう。

△ABCの重心Gについて、\(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=0\)であることを示しましょう。

公式より、重心は\(\displaystyle\frac{\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}}{3}\)です。また\(\overrightarrow{GA}\)、\(\overrightarrow{GB}\)、\(\overrightarrow{GC}\)はそれぞれ以下のように表すことができます。

\(\overrightarrow{GA}=\overrightarrow{a}-\overrightarrow{g}\)
\(\overrightarrow{GB}=\overrightarrow{b}-\overrightarrow{g}\)
\(\overrightarrow{GC}=\overrightarrow{c}-\overrightarrow{g}\)

そこで\(\overrightarrow{g}=\displaystyle\frac{\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}}{3}\)を代入すると以下のようになります。

\(\overrightarrow{GA}=\displaystyle\frac{2\overrightarrow{a}-\overrightarrow{b}-\overrightarrow{c}}{3}\)
\(\overrightarrow{GB}=\displaystyle\frac{-\overrightarrow{a}+2\overrightarrow{b}-\overrightarrow{c}}{3}\)
\(\overrightarrow{GC}=\displaystyle\frac{-\overrightarrow{a}-\overrightarrow{b}+2\overrightarrow{c}}{3}\)

そのため、以下のように計算できます。

\(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\)

\(=\displaystyle\frac{2\overrightarrow{a}-\overrightarrow{b}-\overrightarrow{c}}{3}\)\(+\displaystyle\frac{-\overrightarrow{a}+2\overrightarrow{b}-\overrightarrow{c}}{3}\)\(+\displaystyle\frac{-\overrightarrow{a}-\overrightarrow{b}+2\overrightarrow{c}}{3}\)

\(=0\)

こうして、証明をすることができました。

ベクトルを用いる共線条件

位置ベクトルを用いる計算では、共線条件と共点条件も重要です。ベクトルには向きがあります。また位置ベクトルは原点Oを始点とするため、位置ベクトルを利用すると特定の点を指定できます。つまり、ベクトルの向きだけでなく場所も明確に決まります。

このとき点A、点B、点Pが同じ直線上に存在する場合、以下の関係が成り立ちます。

\(\overrightarrow{AP}=k\overrightarrow{AB}\)

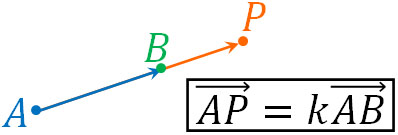
これが共線条件です。点Aが始点であり、\(\overrightarrow{AB}\)を実数倍して\(k\overrightarrow{AP}\)になれば、3点が一つの直線上に存在するのは当然です。それでは、以下の証明問題を解いてみましょう。

△ABCについて、辺ABを\(2:3\)に内分する点をP、辺ACを\(4:3\)に内分する点をQ、辺BCを\(2:1\)に外分する点をRとするとき、3点P、Q、Rが一直線上に存在することを示しましょう。

共線条件より、\(\overrightarrow{PR}=k\overrightarrow{PQ}\)を示すことができれば証明できます。それでは、内分点と外分点の公式を利用して\(\overrightarrow{PQ}\)と\(\overrightarrow{PR}\)を表しましょう。

図を描くと以下のようになります。

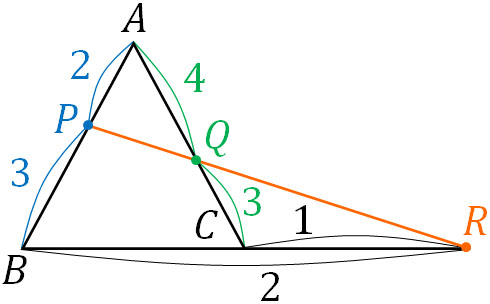
点A、点B、点Cの位置ベクトルを\(\overrightarrow{a}\)、\(\overrightarrow{b}\)、\(\overrightarrow{c}\)とすると、位置ベクトルを以下のように表現できます。

\(\overrightarrow{p}=\displaystyle\frac{3\overrightarrow{a}+2\overrightarrow{b}}{2+3}=\displaystyle\frac{3\overrightarrow{a}+2\overrightarrow{b}}{5}\)
\(\overrightarrow{q}=\displaystyle\frac{3\overrightarrow{a}+4\overrightarrow{c}}{4+3}=\displaystyle\frac{3\overrightarrow{a}+4\overrightarrow{c}}{7}\)
\(\overrightarrow{r}=\displaystyle\frac{-\overrightarrow{b}+2\overrightarrow{c}}{2-1}=-\overrightarrow{b}+2\overrightarrow{c}\)

それでは、位置ベクトルを用いて\(\overrightarrow{PQ}\)と\(\overrightarrow{PR}\)を表しましょう。

\(\overrightarrow{PQ}=\overrightarrow{q}-\overrightarrow{p}\)\(=\displaystyle\frac{3\overrightarrow{a}+4\overrightarrow{c}}{7}-\displaystyle\frac{3\overrightarrow{a}+2\overrightarrow{b}}{5}\)\(=-\displaystyle\frac{6}{35}\overrightarrow{a}-\displaystyle\frac{2}{5}\overrightarrow{b}+\displaystyle\frac{4}{7}\overrightarrow{c}\)

\(\overrightarrow{PR}=\overrightarrow{r}-\overrightarrow{p}\)\(=-\overrightarrow{b}+2\overrightarrow{c}-\displaystyle\frac{3\overrightarrow{a}+2\overrightarrow{b}}{5}\)\(=-\displaystyle\frac{3}{5}\overrightarrow{a}-\displaystyle\frac{7}{5}\overrightarrow{b}+2\overrightarrow{c}\)

こうして、\(\overrightarrow{PR}=\displaystyle\frac{7}{2}\overrightarrow{PQ}\)になるとわかります。そのため3点P、Q、Rは一直線上に存在します。

位置ベクトルが等しいと共点となる：共点条件

位置ベクトルを用いて証明する方法に共点もあります。同じ点であることを証明するためには、位置ベクトルが等しいことを証明すればいいです。位置ベクトルが同じ場合、同じ点を示していることになるからです。これが共点条件です。

それでは、以下の問題を証明しましょう。

△ABCについて、辺AB、BC、CAを\(2:1\)に内分する点をそれぞれD、E、Fとします。△ABCの重心Gと△DEFの重心Hが一致することを証明しましょう。

2つの点が同じであることを証明するため、位置ベクトルを用いて計算しましょう。図を描くと以下のようになります。

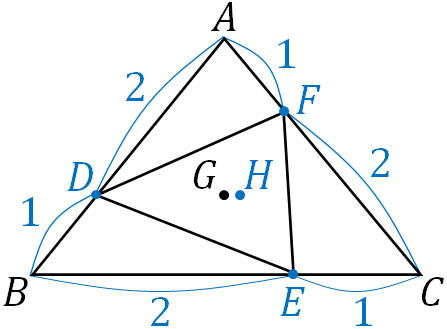
点D、E、Fを位置ベクトルで表すと以下のようになります。

\(\overrightarrow{d}=\displaystyle\frac{\overrightarrow{a}+2\overrightarrow{b}}{2+1}=\displaystyle\frac{\overrightarrow{a}+2\overrightarrow{b}}{3}\)
\(\overrightarrow{e}=\displaystyle\frac{\overrightarrow{b}+2\overrightarrow{c}}{2+1}=\displaystyle\frac{\overrightarrow{b}+2\overrightarrow{c}}{3}\)
\(\overrightarrow{f}=\displaystyle\frac{\overrightarrow{c}+2\overrightarrow{a}}{2+1}=\displaystyle\frac{\overrightarrow{c}+2\overrightarrow{a}}{3}\)

そのため、△DEFの重心Hの位置ベクトルは以下のように計算できます。

\(\overrightarrow{h}=\displaystyle\frac{\displaystyle\frac{\overrightarrow{a}+2\overrightarrow{b}}{3}+\displaystyle\frac{\overrightarrow{b}+2\overrightarrow{c}}{3}+\displaystyle\frac{\overrightarrow{c}+2\overrightarrow{a}}{3}}{3}\)

\(=\displaystyle\frac{\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}}{3}\)

なお、公式より△ABCの重心Gの位置ベクトルは\(\overrightarrow{g}=\displaystyle\frac{\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}}{3}\)です。こうして\(\overrightarrow{g}=\overrightarrow{h}\)となり、重心Gと重心Hは同じ点と証明できました。