高校数学で学ぶ内容に三角形の角の二等分線があります。角を半分にする線を利用して、辺の比を求めるのです。
このとき重要な概念として内分と外分があります。線分の内側に点がある場合、内分点となります。一方、線分の外側に点がある場合は外分点となります。ただ三角形の角の二等分線では、内分でも外分でも公式は同じです。
なお、三角形の角の二等分線を学ぶとき、証明問題がひんぱんに出されます。そこで、角の二等分線の性質を利用して証明できるようにしましょう。
それでは、三角形の角の二等分線を利用してどのように辺の比を求めればいいのでしょうか。線分を内分または外分するときの辺の比と証明方法を解説していきます。
もくじ
線分の内分と外分
線分ABを利用して点Pを置くとき、多くの人は線分AB上の内側に点を置きます。このとき、点Pを内分点といいます。例えば点Pが線分ABを2:3で内分する場合、AP:PB=2:3となります。
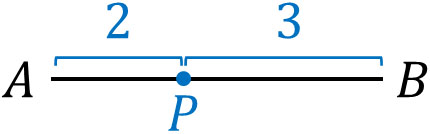
一方、線分ABの延長線上に点Pが存在する場合、点Pを外分点といいます。線分AB上に点Pがないため、以下のようになります。
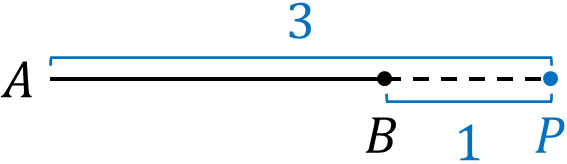
この場合、AP:PB=3:1になります。三角形の角の二等分線を学ぶとき、内分と外分の概念を事前に理解しなければいけません。
三角形の角の二等分線と辺の比には、内分と外分の2種類がある
高校数学では、三角形について内分点や外分点を利用して辺の比を計算します。特に、三角形の角の二等分線を利用します。このとき、以下の2つの定理を理解しましょう。
- 内角の二等分線の定理
- 外角の二等分線の定理
外角の二等分線については少し理解が難しいです。ただ三角形の辺の比を求めたり、証明をしたりする場合、両方の定理を理解しなければいけません。それぞれの定理を確認していきましょう。
内角の二等分線の定理と証明
△ABCについて、∠Aの二等分線と辺BCとの交点をPとします。このとき、AB:AC=BP:CPとなります。これが内角の二等分線の定理です。
例えばAB:AC=3:2の場合、BP:CP=3:2になります。
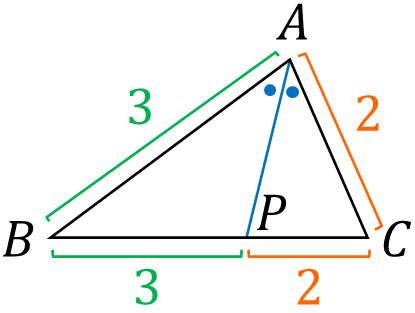
それでは、なぜ内角の二等分線の定理が成り立つのでしょうか。内角の二等分線の定理を証明してみましょう。
証明をするため、点Cを通るAPと平行な線を引きましょう。以下のようになります。
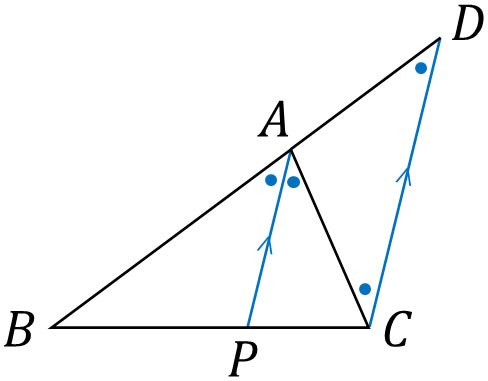
AP//DCより、∠BAP=∠ADC(同意角は等しい)、∠PAC=∠ACD(錯覚は等しい)となります。つまり△ACDは二等辺三角形であり、AC=ADです。
AP//DCなので、BA:AD=BP:CPです(平行線と線分の比)。前述の通りAC=ADなので、BA:AD=BP:CPをBA:AC=BP:CPに変えることができます。こうして、AB:AC=BP:CPを証明することができました。
外角の二等分線の定理と証明
次に外角の二等分線の定理を学びましょう。三角形の内角に対して、内角の外側にあるのが外角です。
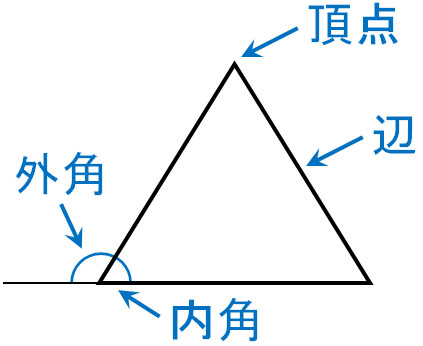
そこで、三角形の外角の二等分線を考えましょう。
△ABCについて、∠Aの外角の二等分線と辺BCの延長線との交点をPとします。この場合、AB:AC=BP:CPとなります。例えばAB:AC=3:2の場合、BP:CP=3:2になります。
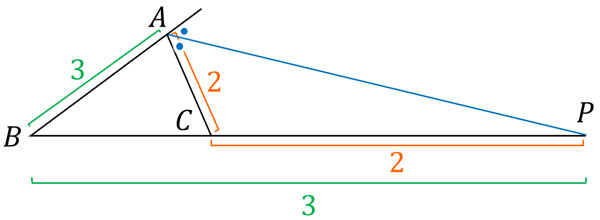
三角形の外角の二等分線と外分点Pには、こうした関係があります。
それでは、外角の二等分線の定理が成り立つことを証明しましょう。先ほどと同じように、点Cを通るように辺APと平行な線を引きましょう。

上図について、AP//DCより、∠ADC=∠EAP(同意角は等しい)、∠ACD=∠CAP(錯覚は等しい)となります。つまり△ACDは二等辺三角形であり、AC=ADです。
AP//DCなので、AB:AD=BP:CPです。またAC=ADなので、AB:ADをAB:ACに入れ替えましょう。そうすると、AB:AC=BP:CPです。こうして、外角の二等分線の定理を証明することができました。
三角形の二等分線について、辺の比を求める
なお三角形の角の二等分線について、内分点であっても外分点であっても、AB:AC=BP:CPとなるのは両方とも共通しています。
内分点であって外分点であっても、角の二等分線では必ず出発点に着目しましょう。その後、到着点と点Pを比較します。例えば△ABCでAB:ACを比較したい場合、∠Aが基準になります。そこで∠Aを出発点とするとき、到着点は点Bと点Cです。このため、AB:ACを作ります。
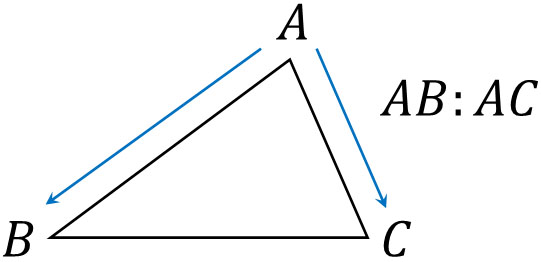
次に、到着点である点Bと点Cについて、点Pを利用してBP:CPを作ります。この場合、内角の二等分線でも外角の二等分線でも、AB:AC=BP:CPとなります。
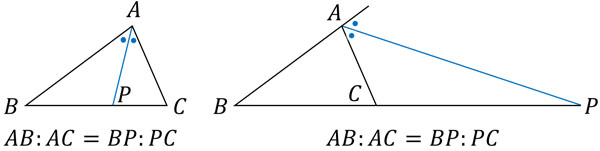
そのため、実質的に内角の二等分線の定理と外角の二等分線の定理は同じ内容と理解していいです。
・三角形の角の二等分線を利用し、辺の比を得る
それでは、実際に問題を解いてみましょう。以下の△ABCについて、∠Aの内角の二等分線と辺BCの交点をD、∠Aの外角の二等分線と辺BCの延長線上との交点をEとするとき、線分DEの長さはいくらでしょうか。
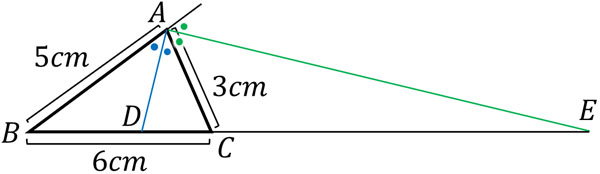
まず、内角の二等分線を利用して線分BDの長さを出しましょう。AB:AC=5:3なので、BD:DC=5:3です。そのため\(BD=a\)とすると、\(5:3=a:6-a\)です。これを解くと、\(a=\displaystyle\frac{15}{4}\)cmです。
\(5:3=a:6-a\)
\(3a=5(6-a)\)
\(3a=30-5a\)
\(8a=30\)
\(a=\displaystyle\frac{15}{4}\)
次に、外角の二等分線を利用してBEの長さを出しましょう。AB:AC=5:3なので、BE:CE=5:3です。\(BE=b\)とすると、\(CE=b-6\)です。そのため、\(5:3=b:b-6\)となります。これを解くと、\(b=15\)になります。
\(5:3=b:b-6\)
\(3b=5(b-6)\)
\(3b=5b-30\)
\(2b=30\)
\(b=15\)
こうして\(BD=\displaystyle\frac{15}{4}\)、\(BE=15\)とわかります。そのため、線分DEの長さは\(\displaystyle\frac{45}{4}\)です。
\(15-\displaystyle\frac{15}{4}=\displaystyle\frac{45}{4}\)
角の二等分線の定理の逆ではどのように問題を解くのか
ここまで解説した内容は角の二等分線の定理です。次に、角の二等分線の定理の逆を解いてみましょう。三角形の辺の比を利用した内分点Pと頂点を結んだ点について、角の二等分線であることを証明するのです。
そこで角の二等分線の定理の逆について、以下の証明問題を解いてみましょう。
- △ABCについて、辺BCをAB:ACの割合に内分する点をPとする。APは∠Aの二等分線であることを証明しましょう。
まず、ABの延長線上にAC=ADとなる線を引きましょう。つまり、二等辺三角形である△ACDを作ります。以下のようになります。
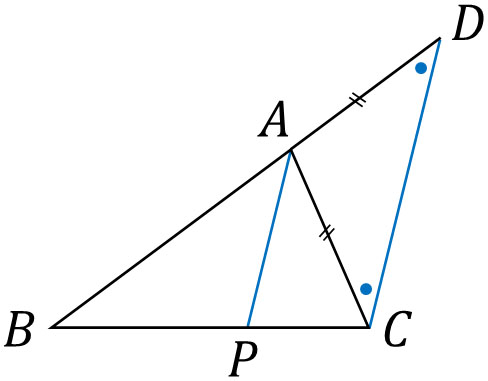
点Pは辺BCをAB:ACの割合に内分するため、AB:AC=BP:PCです。AC=ADなので、ACをADに変えましょう。そうすると、AB:AD=BP:PCになります。AB:AD=BP:PCなので、APとDCは平行です。
AP//DCより、∠BAP=∠ADCであり、∠PAC=∠ACDです。△ACDは二等辺三角形なので、∠ADC=∠ACDです。そのため∠BAP=∠PACであり、APは∠Aの二等分線であることを証明できました。
角の二等分線の定理を利用し、辺の比と証明問題を解く
角の二等分線を利用して問題を解くことがあります。このとき、内分点と外分点を利用して問題を解くようにしましょう。
内分点であっても外分点であっても、考え方は同じです。今回提示した図の場合、両方ともAB:AC=BP:CPになります。そのため外角の二等分線の定理を忘れたとしても、内角の二等分線の定理を利用することによって、辺の比を出すことができます。
また、高校数学で角の二等分線の定理を学ぶとき、証明問題がひんぱんに出されます。そこで、証明問題を解けるようになりましょう。
内分と外分を学ぶとき、最も基本的な定理の一つが角の二等分線の定理です。内分点と外分点の性質を理解し、辺の比を計算し、証明問題を解けるようにしましょう。






