二次曲線と直線：判別式での共有点の個数、弦の長さ

曲線と直線を用いるとき、交点（共有点）の座標を計算しなければいけないことは多いです。そこで放物線や楕円、双曲線について、直線との交点を計算できるようになりましょう。

なお共有点の個数を確認するとき、判別式\(D\)が有効です。判別式は二次関数だけでなく、放物線や楕円、双曲線についても利用できるのです。

また曲線と直線によって交点が作られる場合、弦が作られます。そこで、弦の中点や長さを計算できるようになりましょう。解と係数の関係を利用することにより、弦の中点と長さを得ることができます。

それでは、どのように二次曲線と直線の関係を利用することで計算すればいいのでしょうか。二次曲線と直線を利用して計算問題を解く方法を解説していきます。

1 二次曲線と直線の交点（共有点）の座標を得る
- 1.1 判別式\(D\)を利用して共有点の個数を判断する
2 弦の中点と長さを計算する
- 2.1 弦の中点の軌跡を用いて二次曲線を得る
3 放物線、楕円、双曲線と直線の関係を把握する

二次曲線と直線の交点（共有点）の座標を得る

二次関数は二次曲線と性質がほぼ同じです。実際、放物線の特殊なケースが二次関数です。そのため、二次曲線で共有点の座標を得る方法は二次関数の場合と同じです。

二次関数と直線の交点座標を得たい場合、代入することで計算をします。同じように、二次曲線についても、直線の式を変形後に代入することで座標を計算しましょう。それでは、以下の問題の答えは何でしょうか。

\(y^2=x\)と\(x-2y-3=0\)の交点座標を求めましょう。

\(x-2y-3=0\)を変形すると\(x=2y+3\)です。そこで\(x=2y+3\)を\(y^2=x\)へ代入しましょう。

\(y^2=x\)

\(y^2=2y+3\)

\(y^2-2y-3=0\)

\((y-3)(y+1)=0\)

こうして、\(y=-1,3\)とわかりました。また\(y=-1,3\)であるため、交点座標は\((1,-1)\)と\((9,3)\)です。

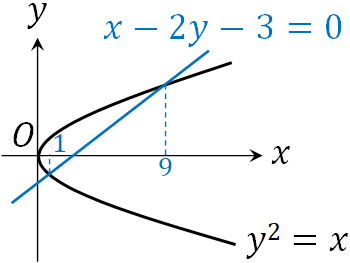
代入して計算すればいいだけなので、交点座標を得るのは簡単です。

判別式\(D\)を利用して共有点の個数を判断する

二次関数と性質が同じであるため、二次曲線では判別式\(D\)を利用することで共有点の個数を判断できます。2つの方程式を連立させた後、判別式\(D\)の値によって共有点の個数を以下のように判断します。

判別式\(D\)が正の値：2つの共有点をもつ
判別式\(D\)が0：1つの共有点をもつ（重解）
判別式\(D\)が負の値：共有点がない

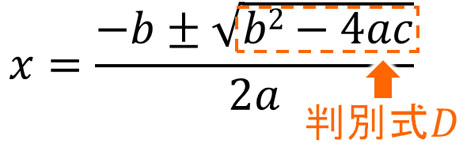
それでは、以下の問題の答えは何でしょうか。

\(x^2+4y^2=20\)と\(y=x+k\)について、共有点の個数を求めましょう。なお、\(k\)は実数です。

\(y=x+k\)を\(x^2+4y^2=20\)に代入しましょう。

\(x^2+4y^2=20\)

\(x^2+4(x+k)^2=20\)

\(5x^2+8kx+4k^2-20=0\)

次に、判別式を用いて計算しましょう。

\(\displaystyle\frac{D}{4}=16k^2-5(4k^2-20)\)

\(=-4k^2+100\)

\(=-4(k^2-25)\)

\(=-4(k+5)(k-5)\)

そのため、答えは以下になります。

\(-5<k<5\)のとき、共有点は2つ
\(k=-5,5\)のとき、共有点は1つ
\(k<-5\)、\(5<k\)のとき、共有点なし

こうして、答えを得ることができました。二次関数と比べて解き方は同じなので、答えを得るのは難しくありません。

弦の中点と長さを計算する

次に、弦の中点を用いて長さを計算しましょう。曲線と直線で2つの共有点がある場合、弦が生成されます。以下の問題の答えは何でしょうか。

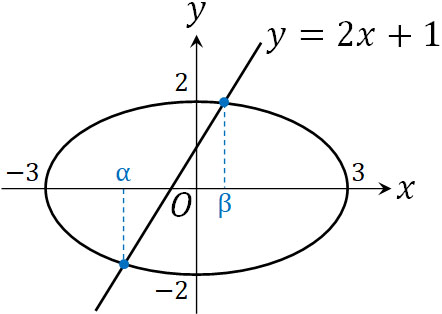
楕円\(\displaystyle\frac{x^2}{9}+\displaystyle\frac{y^2}{4}=1\)と直線\(y=2x+1\)が交わってできる弦の中点の座標と弦の長さを求めましょう。

まず、\(y=2x+1\)を\(\displaystyle\frac{x^2}{9}+\displaystyle\frac{y^2}{4}=1\)へ代入しましょう。

\(\displaystyle\frac{x^2}{9}+\displaystyle\frac{y^2}{4}=1\)

\(4x^2+9y^2=36\)

\(4x^2+9(2x+1)^2=36\)

\(4x^2+9(4x^2+4x+1)=36\)

\(40x^2+36x-27=0\)

\(x\)と\(y\)の値を計算してもいいですが、計算が複雑になるため、解と係数の関係を利用しましょう。2つの解を\(α,β\)とすると以下の関係が成り立ちます。

\(α+β=-\displaystyle\frac{36}{40}=-\displaystyle\frac{9}{10}\)
\(αβ=-\displaystyle\frac{27}{40}\)

中点の\(x\)座標は\(\displaystyle\frac{α+β}{2}\)です。そのため、弦の中点の\(x\)座標は\(-\displaystyle\frac{9}{20}\)とわかります。なお\(y=2x+1\)に代入すると\(y\)座標がわかるため、この式に\(x=-\displaystyle\frac{9}{20}\)を代入しましょう。

\(y=2×-\displaystyle\frac{9}{20}+1\)

\(y=\displaystyle\frac{1}{10}\)

こうして、弦の中点座標は\(\left(-\displaystyle\frac{9}{20},\displaystyle\frac{1}{10}\right)\)とわかります。

なお楕円と直線について、\(x\)軸の交点は\(α,β\)であるため、交点座標は\((α,2α+1)\)と\((β,2β+1)\)です。そこで、座標を用いて以下のように「2つの交点の距離」である弦の長さを計算しましょう。

\(\sqrt{(α-β)^2+\{(2α+1)-(2β+1)\}^2}\)

\(=\sqrt{(α-β)^2+(2α-2β)^2}\)

\(=\sqrt{5(α-β)^2}\)

\(=\sqrt{5\{(α+β)^2-4αβ\}}\)

\(=\displaystyle\sqrt{5\left(\displaystyle\frac{81}{100}+\displaystyle\frac{27}{10}\right)}\)

\(\displaystyle\frac{3\sqrt{195}}{10}\)

こうして、弦の長さを計算することができました。二次関数と二次曲線（放物線、楕円、双曲線）は性質が同じであるため、二次関数の問題を解くときと同じ手順によって計算できます。

弦の中点の軌跡を用いて二次曲線を得る

次に、弦の中点の軌道を用いて二次曲線の方程式を計算しましょう。二次関数でも似た問題を解いたことがあると思いますが、放物線や楕円、双曲線についても軌道の方程式を計算するのです。それでは、以下の問題の答えは何でしょうか。

楕円\(\displaystyle\frac{x^2}{9}+\displaystyle\frac{y^2}{4}=1\)と直線\(y=x-k\)が異なる2点で共有点をもつとき、\(k\)の範囲を求めましょう。また、楕円と直線の共有点によって作られる線分の中点Pの軌道を計算しましょう。

まず、\(y=x-k\)を\(\displaystyle\frac{x^2}{9}+\displaystyle\frac{y^2}{4}=1\)に代入しましょう。

\(\displaystyle\frac{x^2}{9}+\displaystyle\frac{y^2}{4}=1\)

\(4x^2+9y^2=36\)

\(4x^2+9(x-k)^2=36\)

\(13x^2-18kx+9k^2-36=0\)

楕円と直線によって2つの交点が作られるため、判別式を利用することによって\(k\)の範囲がわかります。

\(\displaystyle\frac{D}{4}=81k^2-13(9k^2-36)\)

\(=-36k^2+468\)

\(=-36(k^2-13)\)

\(\displaystyle\frac{D}{4}=-36(k+\sqrt{13})(k-\sqrt{13})\)

こうして、\(k\)の範囲は\(-\sqrt{13}<k<\sqrt{13}\)とわかりました。次に、楕円と直線の共有点によって作られる線分の中点Pの軌道を求めましょう。

2つの共有点の\(x\)座標を\(α,β\)とすると、解と係数の関係より、\(α+β=\displaystyle\frac{18k}{13}\)が成り立ちます。また点Pは中点であるため、点Pの\(x\)座標は以下のようになります。

\(x=\displaystyle\frac{α+β}{2}=\displaystyle\frac{9k}{13}\)

なお点Pは\(y=x-k\)上に存在するため、\(x=\displaystyle\frac{9k}{13}\)を代入すると\(y\)座標を得られます。

\(y=x-k\)

\(y=\displaystyle\frac{9k}{13}-k\)

\(y=-\displaystyle\frac{4k}{13}\)

次に、\(x=\displaystyle\frac{9k}{13}\)と\(y=-\displaystyle\frac{4k}{13}\)を利用して\(k\)を消しましょう。

\(y=-\displaystyle\frac{4k}{13}\)

\(y=-\displaystyle\frac{4}{13}×\displaystyle\frac{13}{9}x\)

\(y=-\displaystyle\frac{4}{9}x\)

こうして、点Pによる軌跡の方程式を得ることができました。

なお\(-\sqrt{13}<k<\sqrt{13}\)であるため、\(-\displaystyle\frac{9\sqrt{13}}{13}<x<\displaystyle\frac{9\sqrt{13}}{13}\)です。この範囲での\(y=-\displaystyle\frac{4}{9}x\)が正解です。