2つの円が平面上に存在するとき、どのような位置関係になるのか理解しましょう。円の半径と中心間の距離を確認することにより、2つの円がどのような位置関係になるのかわかります。2つの円が共有点をもったり、接したりするなど、これらの関係を見分けるのです。
なお円の方程式を利用すれば、2つの円の交点を通る直線を計算したり、2つの円の交点を通る円を得たりすることができます。これらの応用問題を解く方法を学ばなければいけません。
また2つの円の位置関係によって、共通接線の数が変化します。共通接線の数がどのように変わるのかを学び、さらには共通接線の方程式を導き出せるようになりましょう。
数学で2つの円を学ぶとき、位置関係が重要になります。そこで、どのように2つの円に関する図形の問題を解けばいいのか解説していきます。
もくじ
2つの円の位置関係:半径と中心間の距離
2つの円が存在するとき、位置関係には5つのパターンがあります。以下の位置関係になります。
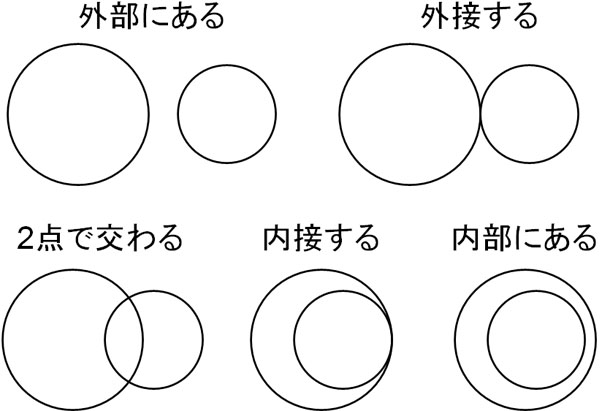
位置関係により、共有点の数が異なります。また、2つの円が外側にあるのか、それとも内側にあるのかも異なります。
それでは、どのようにしてこれらの円の位置関係を把握すればいいのでしょか。円には半径があります。そこで、それぞれの円の半径を\(r_1\)、\(r_2\)とします。また、円の中心間の距離を\(d\)としましょう。
この場合、半径と円の中心間の距離によって以下のように位置関係を分類できます。
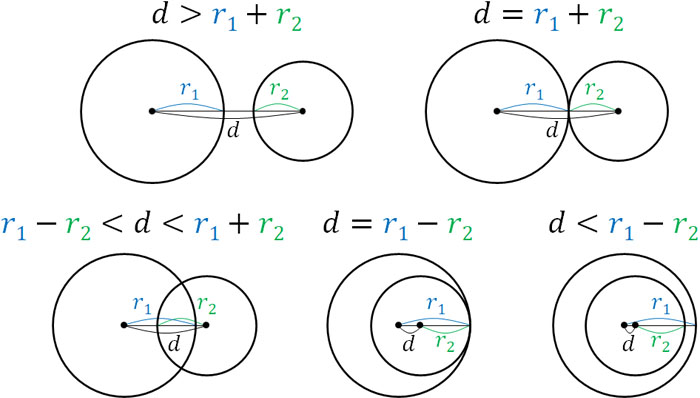
このように、半径と中心間の距離を比較することにより、図形の位置関係がわかります。それでは、以下の問題の答えは何でしょうか。
- \(x^2+y^2=1\)と\((x-a)^2+(y-2)^2=4\)が異なる2点で交わるとき、\(a\)の条件を求めましょう。
\(x^2+y^2=1\)の中心は\((0,0)\)であり、半径は1です。また\((x-a)^2+(y-2)^2=4\)の中心は\((a,2)\)であり、半径は2です。そのため、中心間の距離は以下のように計算できます。
\(\sqrt{(a-0)^2+(2-0)^2}\)
\(=\sqrt{a^2+4}\)
また、2つの円が2点で交わるときは以下の条件を満たす必要があります。
\(2-1<\sqrt{a^2+4}<2+1\)
\(1<\sqrt{a^2+4}<3\)
\(1<a^2+4<9\)
必ず\(1<a^2+4\)となるため、\(a^2+4<9\)に着目すればいいとわかります。\(a^2+4<9\)を解くと、\(-\sqrt{5}<a<\sqrt{5}\)が答えです。
2円の交点を通る円の計算
曲線の方程式として\(f(x)\)と\(g(x)\)がある場合、連立させることによって、2つの曲線の交点を通る曲線(または直線)を得ることができます。言い換えると、定数\(k\)を用いて\(k·f(x)+g(x)=0\)とすると、曲線\(f(x)\)と曲線\(g(x)\)をすべて通る曲線(または直線)を表すことができます。
曲線というのは、円や放物線を含みます。そこで2つの円を利用して、2円の交点を通る円を計算する場合、\(k·f(x)+g(x)=0\)を利用しましょう。それでは、以下の問題の答えは何でしょうか。
- 2円\(x^2+y^2=4\)と\((x+2)^2+(y-2)^2=9\)があります。
- 2つの共有点を通る直線の方程式は何ですか。
- 2つの円の共有点と点\((0,-3)\)を通る円の方程式は何ですか。
1) 2つの共有点を通る直線の方程式は何ですか
\((x+2)^2+(y-2)^2=9\)を以下のように変形しましょう。
\((x+2)^2+(y-2)^2=9\)
\(x^2+y^2+4x-4y-1=0\)
そこで、\(x^2+y^2-4=0\)と\(x^2+y^2+4x-4y-1=0\)を連立させましょう。\(x^2+y^2+4x-4y-1=0\)から\(x^2+y^2-4=0\)を引くと、以下のようになります。
\(4x-4y+3=0\)
\(4x-4y+3=0\)というのは、\(x^2+y^2-4=0\)と\(x^2+y^2+4x-4y-1=0\)による2つの共有点を通る直線を表しています。そのため、答えは\(4x-4y+3=0\)です。
2) 2つの円の共有点と点\((0,-3)\)を通る円の方程式は何ですか
前述の通り、\(k·f(x)+g(x)=0\)によって、\(f(x)\)と\(g(x)\)を通るすべての曲線(または直線)を表すことができます。そこで\(x^2+y^2-4=0\)と\(x^2+y^2+4x-4y-1=0\)について、以下の式を作りましょう。
\(k(x^2+y^2-4)\)\(+(x^2+y^2+4x-4y-1)\)\(=0\)
\(k=-1\)の場合、\(4x-4y+3=0\)を得ることができます。つまり、先ほど計算した「2つの共有点を通る直線」を計算できます。ただ、私たちが得たいのは2つの共有点を通り、点\((0,-3)\)を通る円です。\(k≠-1\)の場合、2つの共有点を通る曲線(今回の問題では円)を得ることができます。
そこで、\(k\)の値が何であれば点\((0,-3)\)を通るのか計算しましょう。点\((0,-3)\)を通るため、先ほどの式に\((0,-3)\)を代入すると以下のようになります。
\(k(x^2+y^2-4)\)\(+(x^2+y^2+4x-4y-1)\)\(=0\)
\(k(0+9-4)+(0+9+0+12-1)=0\)
\(5k+20=0\)
\(k=-4\)
点\((0,-3)\)を通るためには、\(k=-4\)であればいいです。そこで、\(k=-4\)を代入しましょう。
\(-4(x^2+y^2-4)\)\(+(x^2+y^2+4x-4y-1)\)\(=0\)
\(-3x^2-3y^2+4x-4y+15=0\)
\(3x^2+3y^2-4x+4y-15=0\)
こうして、ひとつの点と2つの共有点を通る円の方程式を得ることができました。
円と直線の交点を通る円
先ほど、2つの円に対する共有点を利用し、共有点を通る円の方程式を計算しました。それでは、円と直線の共有点に対して、共有点を通る円はどのように計算すればいいのでしょうか。方法は同じであり、\(k·f(x)+g(x)=0\)を利用しましょう。
以下の問題の答えは何でしょうか。
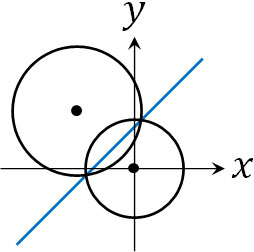
- 円\(x^2+y^2=25\)と直線\(y=x+1\)について、2つの交点と原点Oを通る円の方程式を求めましょう。
\(f(x)=x-y+1\)、\(g(x)=x^2+y^2-25\)とすると、円と直線の交点を通る曲線を以下のように表すことができます。
\(k(x-y+1)+(x^2+y^2-25)=0\)
原点を通るため、\((0,0)\)を代入しましょう。すると、\(k=25\)となります。\(k=25\)を代入すると以下のようになります。
\(25(x-y+1)+(x^2+y^2-25)=0\)
\(x^2+y^2+25x-25y=0\)
こうして、2つの共有点を通り、かつ原点Oを通る円の方程式を得ることができました。
2つの円に対する共通接線の本数
2つの円の位置関係については、共有接線の本数を考えるときも重要です。以下のように、円の位置関係によって共有接線の数が変化するからです。
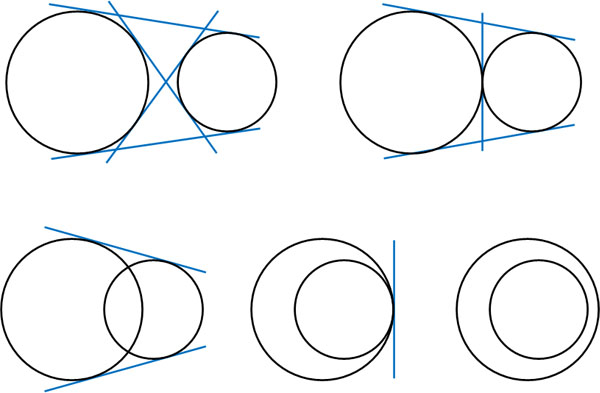
このように、共通接線の数は1つずつ変化します。2つの円について、共有接線の最大数は4であり、最小数は0です。
数学で問題を解くとき、事前に答えの数を知っていると便利です。そこで、円の位置関係と共有接線の数を把握しましょう。
共通接線を得る練習問題
それでは2つの円について、共有接線を得るにはどのように計算すればいいのでしょうか。実際に問題を解くことにより、共有接線を得る方法を確認しましょう。
- 2円\(x^2+y^2=4\)と\((x-4)^2+y^2=1\)の共有接線の方程式を求めましょう。
図を描くと、以下のように共有接線は4つであるとわかります。
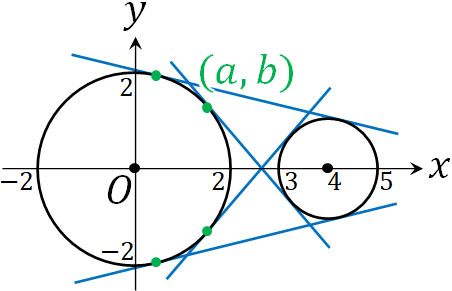
まず、円\(x^2+y^2=4\)と共有接線の交点座標を\((a,b)\)としましょう。\((a,b)\)は円上の点であるため、\(a^2+b^2=4\)が成り立ちます。
また公式を利用すると、円\(x^2+y^2=4\)上の点\((a,b)\)の接線は\(ax+by=4\)となります。なお接線と円の中心との距離は円の半径です。つまり、\(ax+by-4=0\)と円\((x-4)^2+y^2=1\)の中心\((4,0)\)との距離は1となる必要があるため、点と直線の距離を得る公式を利用して以下のように計算しましょう。
\(\displaystyle\frac{|4a+0-4|}{\sqrt{a^2+b^2}}=1\)
\(\displaystyle\frac{|4a-4|}{\sqrt{a^2+b^2}}=1\)
\(a^2+b^2=4\)であるため、以下のように計算しましょう。
\(\displaystyle\frac{|4a-4|}{\sqrt{4}}=1\)
\(|4a-4|=2\)
\(|2a-2|=1\)
\(2a-2=±1\)
\(a=\displaystyle\frac{1}{2},\displaystyle\frac{3}{2}\)
・\(a=\displaystyle\frac{1}{2}\)の場合
\(a^2+b^2=4\)より、以下のように計算しましょう。
\(\displaystyle\frac{1}{4}+b^2=4\)
\(b^2=\displaystyle\frac{15}{4}\)
\(b=±\displaystyle\frac{\sqrt{15}}{2}\)
\(a=\displaystyle\frac{1}{2}\)、\(b=±\displaystyle\frac{\sqrt{15}}{2}\)であるため、接線の方程式は以下のようになります。
\(ax+by=4\)
\(\displaystyle\frac{x}{2}±\displaystyle\frac{\sqrt{15y}}{2}=4\)
\(x±\sqrt{15}y=8\)
・\(a=\displaystyle\frac{3}{2}\)の場合
\(a^2+b^2=4\)より、以下のように計算しましょう。
\(\displaystyle\frac{9}{4}+b^2=4\)
\(b^2=\displaystyle\frac{7}{4}\)
\(b=±\displaystyle\frac{\sqrt{7}}{2}\)
\(a=\displaystyle\frac{3}{2}\)、\(b=±\displaystyle\frac{\sqrt{7}}{2}\)であるため、接線の方程式は以下のようになります。
\(ax+by=4\)
\(\displaystyle\frac{3x}{2}±\displaystyle\frac{\sqrt{7y}}{2}=4\)
\(3x±\sqrt{7}y=8\)
こうして、4つの接線の方程式を得ることができました。答えの数を事前に予測できているため、答えが4つあっても問題ないとわかります。
2つの円を利用する問題を解けるようになる
2つの円が関わる問題では、円の位置関係を把握しましょう。円の半径と中心との距離を比較することによって、どのような位置関係になっているのかわかるのです。
また2つの曲線の交点を通る曲線や直線について、定数\(k\)を利用することで表せます。2つの曲線の方程式がそれぞれ\(f(x)\)と\(g(x)\)なのであれば、\(k·f(x)+g(x)=0\)を利用することで計算しましょう。
なお2つの円がある場合、共通接線を引くことができます。ただ、2つの円の位置関係によって共通接線の数が変化します。そこで、共通接線の数が何本になるのか把握できるようになりましょう。これにより、共通接線の方程式を計算するとき、答えの数を事前に予想できます。
2つの円を利用する問題では、円の位置関係が重要であり、解き方があります。そこで、どのように計算すればいいのか学びましょう。






