位置ベクトルを利用することにより、特定の点を表すことができます。このとき、ベクトルの終点がどこに存在するのか把握できるようになりましょう。
ベクトルの終点の存在範囲では、いくつかのパターンに分けて考える必要があります。また、ベクトルの性質を学ぶことにより、終点の存在範囲がわかるようになります。係数の和が1になるようにしたり、式を変形したりすることで計算できるようにするのです。
なおベクトルの終点の存在範囲では、三角形だけでなく、平行四辺形での範囲を計算しなければいけないこともあります。
それでは、ベクトルの終点の存在範囲を知るにはどのようにすればいいのでしょうか。ベクトルの終点を得る方法を解説していきます。
もくじ
直線AB上に点Pが存在するケース
ベクトルの終点の存在範囲を学ぶとき、重要な考え方に「係数の和を1にする」ことがあります。ベクトル方程式を含め、係数を1にすることは重要です。
2つのベクトルを利用すれば、あらゆるベクトルを表現できます。例えば、以下のように3つのベクトルがあるとします。

\(\overrightarrow{a}\)を作るとき、\(\overrightarrow{b}\)を\(k\)倍、\(\overrightarrow{c}\)を\(l\)倍すると以下のようになります。
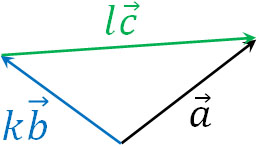
2つのベクトルを利用すれば、すべてのベクトルを表現できることは問題なく理解できると思います。このとき、特定のベクトルを表したいときは条件を加えましょう。
ベクトル方程式を学ぶとき、直線を表せるベクトル方程式の公式を覚えることになります。このとき、点A(\(\overrightarrow{a}\))と点B(\(\overrightarrow{b}\))を結ぶ辺AB上に点P(ベクトルの終点)が存在するのであれば、ベクトルの終点である点P(\(\overrightarrow{p}\))を以下のように表現します。
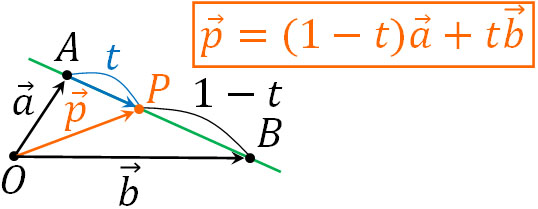
重要なのは、点A(\(\overrightarrow{a}\))の位置ベクトルと点B(\(\overrightarrow{b}\))の位置ベクトルについて、係数を足すと1になるという事実です。上図では、\(\overrightarrow{a}\)の係数は\(1-t\)であり、\(\overrightarrow{b}\)の係数は\(\overrightarrow{t}\)です。そのため、足すと1になります。
なお、辺AB上にある点P(\(\overrightarrow{p}\))をほかの方法で表すと以下のようになります。
- \(\overrightarrow{p}=s\overrightarrow{a}+t\overrightarrow{b}\)
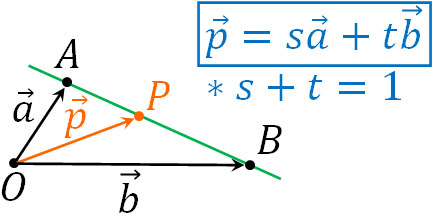
この式について、必ず\(s+t=1\)となります。要は、「2つの位置ベクトルについて、係数を足して1になる場合、必ず2点を結ぶ線上に点P(ベクトルの終点)が存在する」と理解しましょう。
内分点の公式を利用して計算するときであっても、2つの係数を足すと必ず1になります。これは、2つの点を結ぶ線上に点Pが存在するからなのです。
三角形の辺上にベクトルの終点が存在する場合
なお、場合によっては以下の条件が提示されることがあります。
- \(\overrightarrow{p}=s\overrightarrow{a}+t\overrightarrow{b}\)
- \(s+t=1\)、\(s≧0\)、\(t≧0\)
\(s+t=1\)に加えて、\(s≧0\)と\(t≧0\)も満たす必要があります。そのため言い換えると、以下の条件になります。
- \(\overrightarrow{p}=s\overrightarrow{a}+t\overrightarrow{b}\)
- \(s+t=1\)、かつ\(0≦s≦1\)、\(0≦t≦1\)
例えば\(s=0,t=1\)のとき、点Pは\(\overrightarrow{p}=\overrightarrow{b}\)となります。これはつまり、点Pが点Bの上に存在することを意味しています。また\(s=1,t=0\)のとき、点Pは\(\overrightarrow{p}=\overrightarrow{a}\)となります。そのため、点Pは点Aの上にあります。
そのため\(s+t=1\)、\(s≧0\)、\(t≧0\)となる場合、以下のようにベクトルの終点は線分AB上になります。
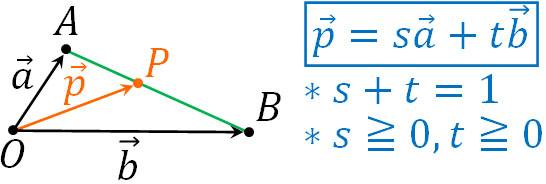
条件が\(s+t=1\)だけの場合、点Pは線分ABの外に存在することがひんぱんにあります。辺ABの直線上であれば、どこに点Pが存在してもいいのです。一方で\(s≧0\)と\(t≧0\)が条件に加わると、点Pは線分AB上に存在することになります。
三角形の周または内部に点Pが存在するケース
不等号を用いて、ベクトルの終点の存在範囲を表すケースもあります。以下がこれに該当します。
- \(\overrightarrow{p}=s\overrightarrow{a}+t\overrightarrow{b}\)
- \(s+t≦1\)、\(s≧0\)、\(t≧0\)
\(s+t=1\)では、前述のとおり点Pは線分AB上に存在します。それに対して\(s+t<1\)の場合、点Pは三角形の内部に存在することになります。
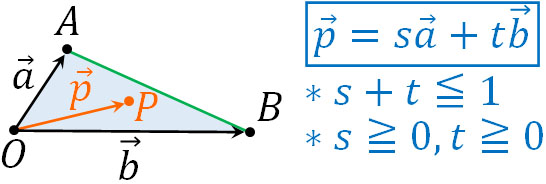
例えば\(\overrightarrow{p}=\displaystyle\frac{1}{4}\overrightarrow{a}+\displaystyle\frac{1}{4}\overrightarrow{b}\)では以下のようになります。
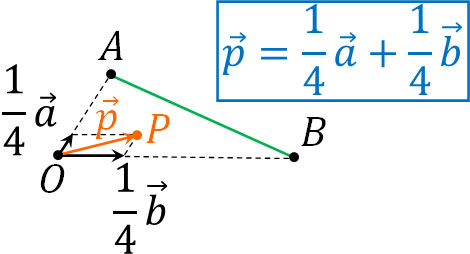
\(s+t≦1\)が条件の場合、点は辺の上だけでなく、内部に存在する可能性があります。
係数を確認し、ベクトルの存在範囲を得る
それでは、実際に練習問題を解いてみましょう。以下の問題の答えは何でしょうか。
- △OABについて、\(\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}\)です。実数\(s,t\)が\(2s+t=3\)を満たすとき、点Pの存在範囲を図示しましょう。
先ほどとは異なり、\(2s+t=3\)となっています。つまり係数が異なりますし、足しても1になりません。そこで、係数を足して1になるように式を変えましょう。両辺を3で割れば、以下のように右辺に1を作ることができます。
- \(\displaystyle\frac{2}{3}s+\displaystyle\frac{1}{3}t=1\)
ただ式を確認すると\(\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}\)であるため、\(\displaystyle\frac{2}{3}s\)や\(\displaystyle\frac{1}{3}t\)は存在しません。そこで以下のように式を変形することで、\(\displaystyle\frac{2}{3}s\)と\(\displaystyle\frac{1}{3}t\)を作りましょう。
- \(\overrightarrow{OP}=\color{red}{\displaystyle\frac{2}{3}s}·\displaystyle\frac{3}{2}\overrightarrow{OA}+\color{red}{\displaystyle\frac{1}{3}t}·3\overrightarrow{OB}\)
\(\displaystyle\frac{2}{3}s+\displaystyle\frac{1}{3}t=1\)となり、上のように変形することで、ベクトルの係数と式を合わせることができました。
仮に\(\displaystyle\frac{2}{3}s=1\)のとき、点Pは\(\displaystyle\frac{3}{2}\overrightarrow{OA}\)の場所にあります。また\(\displaystyle\frac{1}{3}t=1\)のとき、点Pは\(3\overrightarrow{OB}\)の場所にあります。つまり、点Pは\(\displaystyle\frac{3}{2}\overrightarrow{OA}\)と\(3\overrightarrow{OB}\)を結ぶ直線上に存在します。

ベクトルの終点の存在範囲を得たいとき、係数を足して1になるように式を調節しましょう。その後、式の中に新たな係数を作りましょう。これにより、点Pの存在範囲がわかるようになります。
平行四辺形の周または内部に点Pが存在するケース
ここまで、三角形を利用する場合について、ベクトルの終点の存在範囲を確認しました。次に、平行四辺形となるベクトルの終点の存在範囲を確認しましょう。以下の条件がこれに該当します。
- \(\overrightarrow{p}=s\overrightarrow{a}+t\overrightarrow{b}\)
- \(0≦s≦1\)、\(0≦t≦1\)
先ほどとは異なり、\(s+t=1\)が条件に存在しません。つまり\(s=1,t=1\)となることが可能であり、この場合は\(s+t=2\)となります。この条件では、三角形ではなく以下のような平行四辺形がベクトルの終点の存在範囲です。

それでは、以下の問題の答えは何でしょうか。
- △OABについて、\(\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}\)、\(1≦s≦2\)、\(0≦t≦1\)を満たす点Pの存在範囲を図示しましょう。
\(s+t\)の範囲は記されていません。また、\(s\)と\(t\)は独立しています。そこで、まずは\(1≦s≦2\)となる範囲を考えましょう。\(1≦s≦2\)であるため、下図では点Aから点Dまでが範囲です。
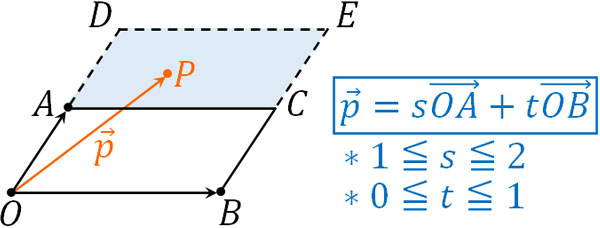
一方、\(0≦t≦1\)であるため、\(t\overrightarrow{OB}\)は原点から点Bまでが範囲です。ただ前述のとおり、\(1≦s≦2\)であるため、点Pの始点は点Aです。そこで、点Aを基準にして\(\overrightarrow{OB}\)の範囲を確認すると、上図の平行四辺形ADECが点Pの存在範囲になります。
係数が複雑な場合のベクトルの終点の存在範囲
次に、係数が少し複雑になっている場合の終点の存在範囲を確認しましょう。以下の問題の答えは何でしょうか。
- △OABについて、\(\overrightarrow{OP}=s\overrightarrow{OA}+(s+t)\overrightarrow{OB}\)、\(0≦s≦1\)、\(0≦t≦1\)を満たす点Pの存在範囲を図示しましょう。
以下のように式を変形しましょう。
\(\overrightarrow{OP}=s\overrightarrow{OA}+(s+t)\overrightarrow{OB}\)
\(\overrightarrow{OP}=s(\overrightarrow{OA}+\overrightarrow{OB})+t\overrightarrow{OB}\)
なお\(\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{OC}\)とすると、式を以下のように変形できます。
- \(\overrightarrow{OP}=s\overrightarrow{OC}+t\overrightarrow{OB}\)
こうして、平行四辺形でのベクトルの終点の存在範囲と同じ式を作ることができました。\(\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{OC}\)であるため、図を作ると、平行四辺形OACBにて、点Cは点Oの反対側にあるとわかります。

そこで△OBCについて、以下の条件での点Pの存在範囲を図示しましょう。
- \(\overrightarrow{OP}=s\overrightarrow{OC}+t\overrightarrow{OB}\)
- \(0≦s≦1\)、\(0≦t≦1\)
そうすると、△OBCを利用して作ることのできる以下の図(平行四辺形)が答えであるとわかります。
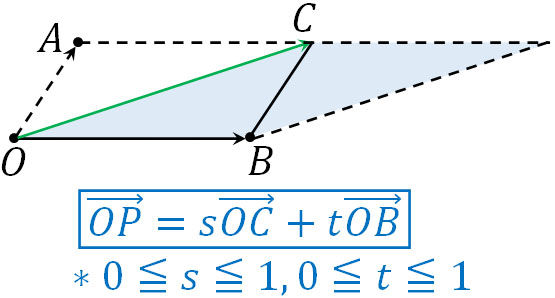
こうして、\(\overrightarrow{OB}\)と\(\overrightarrow{OC}\)を2辺とする平行四辺形がベクトルの終点の存在範囲とわかりました。
ベクトルの終点の存在範囲を計算する
点として位置ベクトルを表すとき、点がどの場所に存在する可能性があるのか学びましょう。ベクトルの終点の存在範囲というのは、どの場所に点Pが存在できるのかを意味します。
ベクトルの終点の存在範囲では複数のパターンを覚えましょう。条件によって、点Pが存在する場所が異なります。条件が違えば、辺ABではなく、線分AB上に点Pが存在するようになります。場合によっては、ベクトルの終点の存在範囲が平行四辺形になることもあります。
なおベクトルの終点の存在範囲を計算するとき、係数の和が1にならないケースがひんぱんにあります。そこで係数の和を1に変え、式を変形することで点Pの存在範囲を確認しましょう。
解き方を覚えていないと、点Pの範囲を図示するのは難しいです。そこで\(s\)や\(t\)の条件や係数を確認することで答えを得ましょう。