ベクトルを利用することで円を表現することができます。そこで円の方程式だけでなく、円のベクトル方程式を利用できるようになりましょう。
直線のベクトル方程式と同じように、円をベクトルで表す方法はいくつかあります。そのため、すべての方法を利用できるようにならなければいけません。また、円のベクトル方程式を円の方程式へ変換できるようになりましょう。
なお円の方程式を利用するとき、接線を利用して計算するケースがあります。ベクトル方程式についても、円で利用される性質を用いて接線に関わる計算問題を解ける必要があります。
それでは、円のベクトル方程式の公式はどのようになっているのでしょうか。また、どのように計算問題を解けばいいのでしょうか。円のベクトル方程式を解説していきます。
もくじ
円のベクトル方程式の公式
それでは、どのように円のベクトル方程式を利用すればいいのでしょうか。点Cが円の中心であり、点Pの位置が円周上の場合、\(\overrightarrow{CP}\)と記すことで円の中心Cから円周上までのベクトルを記すことができます。
また、CPの長さは半径\(r\)になります。そこで、線分CPの長さを表す\(|\overrightarrow{CP}|\)を利用して以下のように式を作りましょう。
- \(|\overrightarrow{CP}|=r\)
なお、位置ベクトルを利用すると式を以下のように変形できます。
- \(|\overrightarrow{p}-\overrightarrow{c}|=r\)

こうして、円のベクトル方程式を導出できました。円のベクトル方程式をどのように導き出せるのか学べば、公式を覚える必要はありません。図形を利用して公式を作ることができます。
それでは次に、両辺を二乗してみましょう。
\(|\overrightarrow{p}-\overrightarrow{c}|^2=r^2\)
\((\overrightarrow{p}-\overrightarrow{c})^2=r^2\)
こうして、2つ目の公式である\((\overrightarrow{p}-\overrightarrow{c})^2=r^2\)を得ることができました。二乗するだけであるため、簡単に公式を導出できます。
それでは、以下の問題を解いてみましょう。
- 点C(\(\overrightarrow{c}\))を中心とする半径\(r\)の円について、任意の点をP(\(\overrightarrow{p}\))とするとき、\(|3\overrightarrow{p}-\overrightarrow{c}|=6\)はどのような円でしょうか。
\(\overrightarrow{p}\)は中心からの距離を表し、基準になります。そこで、\(\overrightarrow{p}\)の係数を1にしましょう。そうすると、以下のようになります。
- \(\left|\overrightarrow{p}-\displaystyle\frac{1}{3}\overrightarrow{c}\right|=2\)
つまり、以下の図で線分OCを\(\displaystyle\frac{1}{3}\)倍した場所が中心であり、半径2の円であるとわかります。
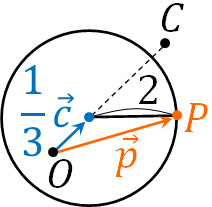
点Cの場所によって、円の場所は変化します。ただいずれにしても、ベクトル方程式を利用することで円の性質がわかります。
ベクトル方程式を円の方程式に変換する
円のベクトル方程式は円の方程式に変換することができます。一つの円について、円の方程式でもベクトル方程式でも表現できるのです。
中心Cの座標を\((a,b)\)、点Pの座標を\((x,y)\)とします。この場合、\(\overrightarrow{CP}=\overrightarrow{p}-\overrightarrow{c}\)を成分で表すと以下のようになります。
- \(x\)成分:\((x-a)\)
- \(y\)成分:\((y-b)\)
そのため、以下のように式を変形できます。
\((\overrightarrow{p}-\overrightarrow{c})^2=r^2\)
\((x-a,y-b)^2=r^2\)
\((x-a)^2+(y-b)^2=r^2\)
こうして、円の方程式を作ることができました。円の方程式と円のベクトル方程式について、どちらを利用するほうが最適なのかは問題によって異なります。ただいずれにしても、ベクトル方程式と円の方程式の変換を行えるようになることは重要です。
直径の両端がわかっている場合のベクトル方程式
なお場合によっては、直径の両端がわかっているケースがあります。円の中心を通る直線(直径)について、両端の点をそれぞれA(\(\overrightarrow{a}\))、B(\(\overrightarrow{b}\))とします。円周上の任意の点をP(\(\overrightarrow{p}\))とすると、APとBPは垂直であるため、ベクトルの内積はゼロになります。
\(\overrightarrow{AP}·\overrightarrow{BP}=0\)であるため、以下の式を作りましょう。
- \((\overrightarrow{p}-\overrightarrow{a})·(\overrightarrow{p}-\overrightarrow{b})=0\)
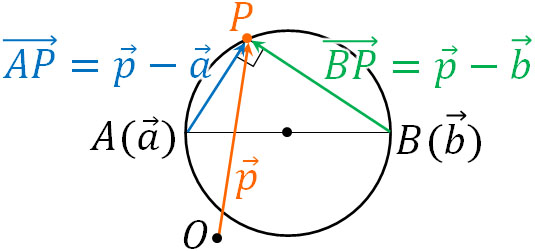
こうして、円のベクトル方程式の公式を導出できました。この公式についても覚える必要はなく、どのように円のベクトル方程式を作ればいいのか学びましょう。
それでは、例題として以下の問題を解きましょう。
- 2点\((2,3)\)、\((4,1)\)が直径の両端であるとき、円の方程式を求めましょう。
ベクトル方程式を利用しなくても円の方程式を得ることができます。ただ、ここでは円のベクトル方程式を用いて円の方程式を計算しましょう。円周上の点をP\((x,y)\)とすると、以下のようになります。
- \(\overrightarrow{AP}=\overrightarrow{p}-\overrightarrow{a}=(x-2,y-3)\)
- \(\overrightarrow{BP}=\overrightarrow{p}-\overrightarrow{b}=(x-4,y-1)\)
そこで、以下のように計算しましょう。
\(\overrightarrow{AP}·\overrightarrow{BP}=0\)
\((\overrightarrow{p}-\overrightarrow{a})·(\overrightarrow{p}-\overrightarrow{b})=0\)
\((x-2)(x-4)+(y-3)(y-1)=0\)
\((x^2-6x+8)+(y^2-4y+3)=0\)
\((x-3)^2+(y-2)^2=2\)
こうして、円のベクトル方程式を利用することによって円の方程式を得ることができました。
円の接線とベクトル方程式
円では接線に関する問題もひんぱんに出題されます。そこで、円の接線のベクトル方程式を学びましょう。
円の中心をC(\(\overrightarrow{c}\))、接線との円周上の接点をP0(\(\overrightarrow{p_0}\))、接線上の任意の点をP(\(\overrightarrow{p}\))とします。この場合、\(\overrightarrow{CP_0}·\overrightarrow{P_0P}\)\(=0\)となるため、以下の関係が成り立ちます。
- \(\overrightarrow{CP_0}·\overrightarrow{P_0P}=(\overrightarrow{p_0}-\overrightarrow{c})·(\overrightarrow{p}-\overrightarrow{p_0})\)\(=0\)
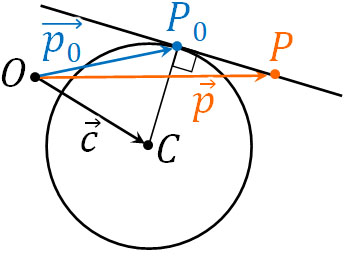
こうして、円の接線のベクトル方程式を得ることができました。
次に、円の接線をほかのベクトル方程式で表しましょう。先ほどの条件に加えて、半径を\(r\)とします。また下図のように角度\(θ\)を加えます。
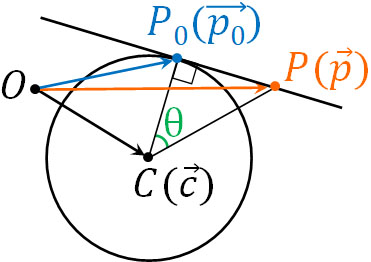
上図より、\(|\overrightarrow{CP}|cosθ=|\overrightarrow{CP_0}|\)です。そこで、両辺に\(|\overrightarrow{CP_0}|\)をかけましょう。
- \(|\overrightarrow{CP}||\overrightarrow{CP_0}|cosθ=|\overrightarrow{CP_0}|^2\)
ベクトルの内積の公式より、\(\overrightarrow{CP}·\overrightarrow{CP_0}=|\overrightarrow{CP}||\overrightarrow{CP_0}|cosθ\)です。そこで、この式を代入して計算しましょう。
\(|\overrightarrow{CP}||\overrightarrow{CP_0}|cosθ=|\overrightarrow{CP_0}|^2\)
\(\overrightarrow{CP}·\overrightarrow{CP_0}=|\overrightarrow{CP_0}|^2\)
\((\overrightarrow{p}-\overrightarrow{c})·(\overrightarrow{p_0}-\overrightarrow{c})=|\overrightarrow{CP_0}|^2\)
なお\(|\overrightarrow{CP_0}|\)は半径\(r\)であるため、以下の式を得られます。
- \((\overrightarrow{p}-\overrightarrow{c})·(\overrightarrow{p_0}-\overrightarrow{c})=r^2\)
こうして、円の接線に関する2つ目のベクトル方程式を得ることができました。
ベクトル方程式から、円の接線の方程式に関する公式を導出する
それでは円の接線のベクトル方程式を利用して、円の接線を得る方程式を計算しましょう。ベクトル方程式を\(x\)成分、\(y\)成分に分けて計算することにより、円の接線の公式を得ることができます。
接点P0を\(\overrightarrow{p_0}=(x_0,y_0)\)、接線上の点Pを\(\overrightarrow{p}=(x,y)\)、中心Cを\(\overrightarrow{c}=(a,b)\)とします。そうすると、以下のようになります。
- \(\overrightarrow{p}-\overrightarrow{c}=(x-a,y-b)\)
- \(\overrightarrow{p_0}-\overrightarrow{c}=(x_0-a,y_0-b)\)
前述のとおり、\((\overrightarrow{p}-\overrightarrow{c})·(\overrightarrow{p_0}-\overrightarrow{c})=r^2\)です。そこで、先ほど計算した\(x\)成分、\(y\)成分を代入しましょう。
- \((x-a)(x_0-a)+(y-b)(y_0-b)\)\(=r^2\)
こうして、円の接線の方程式を得ることができました。参考までに、中心が原点のときは\(\overrightarrow{c}=(0,0)\)です。この場合、以下の公式となります。
- \(xx_0+yy_0=r^2\)
このように円の接線のベクトル方程式を利用することにより、円の接線の方程式を得るための公式を導出できました。
円のベクトル方程式を利用する
直線のベクトル方程式だけでなく、円のベクトル方程式を覚えなければいけません。ただ直線のベクトル方程式よりも、円のベクトル方程式のほうが公式の作り方は簡単です。公式の暗記は意味がなく、図形を利用して公式を作れるようになりましょう。
円のベクトル方程式には主に2種類あります。このとき中心や半径がわかっていなくても、直径の両端の位置ベクトルがわかっていれば円のベクトル方程式を利用できます。
なおベクトルの性質を利用して、円の接線のベクトル方程式を導出できるようになりましょう。また円のベクトル方程式を利用することにより、円の接線のベクトル方程式を得られるだけでなく、円の方程式を作ることもできます。
円のベクトル方程式を利用することにより、どのような形状の円なのか把握できるようになりましょう。円のベクトル方程式と円の方程式の両方を利用できるようになれば、さまざまな方法で問題を解けるようになります。