図形では、円と直線に関する問題を出題されることがあります。円と直線の位置関係や距離を計算するのです。
判別式を利用することにより、円と直線が共有点をもつかどうかを判断できます。直線の方程式を円の方程式へ代入することにより、解を得たり、共有点の数を把握したりできるのです。また、円と直線の位置関係も理解できます。
場合によっては、直線が円に対して接線となるケースがあります。円の接線については、公式があります。そこで、円の接線の方程式を得る公式を利用することによって問題を解けるようになりましょう。
それでは、円と直線の関係を利用してどのように計算問題を解けばいいのでしょうか。直線と円の方程式を利用して問題を解く方法を解説していきます。
もくじ
直線の方程式を円の方程式に代入し、解を得る
2つの直線の交点を得るためには、連立方程式を解けばいいです。言い換えると、一方の式に代入することによって答えを得ることができます。
直線と円の交点についても、直線の方程式を円の方程式に代入することで解を計算できます。代入することにより、2つの方程式を満たす解を得ることができるのです。それでは、以下の問題の答えは何でしょうか。
- 円\(x^2+y^2=4\)と直線\(y=x+2\)の交点座標を求めましょう。
答えを得るため、直線の方程式を円の方程式に代入しましょう。
\(x^2+(x+2)^2=4\)
\(2x^2+4x=0\)
\(x(x+2)=0\)
こうして、\(x=-2,0\)で円と直線が交わるとわかりました。また\(x\)座標を利用して\(y\)座標を計算しましょう。そうすると、\((-2,0)\)と\((0,2)\)が答えとわかります。
円と直線の位置関係:判別式を利用して解の数を確認する
場合によっては、交点の座標を計算する必要はなく、円と直線の位置関係を知ることができれば十分なケースもあります。その場合、判別式を利用しましょう。
円と直線の位置関係では、主に以下の3種類があります。
- 円と直線が2点で交わる
- 円と直線が1点で交わる:円と直線が接する
- 円と直線は共有点をもたない
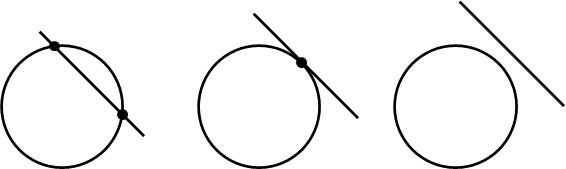
このように、それぞれ位置関係が異なります。また直線の方程式を円の方程式に代入すると、二次方程式を得られます。このとき、二次方程式の解があるかどうかを確認する方法として判別式\(D\)が利用されます。そのため、判別式と解の数には以下の関係があります。
- \(D>0\):円と直線が2点で交わる
- \(D=0\):円と直線が1点で交わる:円と直線が接する
- \(D<0\):円と直線は共有点をもたない
それでは、以下の問題を解いてみましょう。
- 円\(x^2+y^2=4\)と直線\(y=2x+k\)が2つの共有点をもつとき、定数\(k\)の範囲を求めましょう。
円と直線の交点を計算するためには、前述の通り直線の方程式を円の方程式に代入する必要があります。そこで、以下のように計算しましょう。
\(x^2+(2x+k)^2=4\)
\(5x^2+4kx+k^2-4=0\)
この二次方程式が解を2つもてば、円と直線は2つの共有点をもつことになります。そこで、判別式を利用しましょう。
\((4k)^2-4×5×(k^2-4)>0\)
\(16k^2-20k^2+80>0\)
\(-k^2+20>0\)
\(k^2<20\)
\(-2\sqrt{5}<k<2\sqrt{5}\)
こうして、\(-2\sqrt{5}<k<2\sqrt{5}\)のときに円と直線は2つの共有点をもつとわかります。
・円の中心と直線との距離の関係
なお場合によっては、判別式を利用しなくても円と直線の位置関係を把握できるケースがあります。具体的には、円の半径\(r\)と円と直線の距離\(d\)を比較します。円の半径\(r\)と円と直線の距離\(d\)には以下の関係があります。
- \(d<r\):円と直線が2点で交わる
- \(d=r\):円と直線が1点で交わる:円と直線が接する
- \(d>r\):円と直線は共有点をもたない
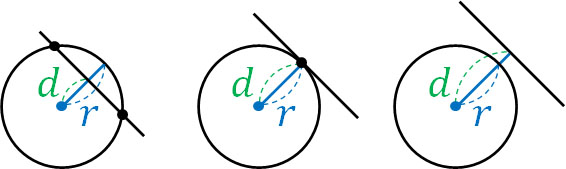
当たり前の内容ではありますが、この関係を理解しましょう。
点と直線の距離を利用して計算する
円と直線を利用するため、点と直線の距離を利用して計算問題を解くケースは多いです。円の中心から直線の距離であったり、円上の点から直線との距離であったり、これらの距離を利用して問題を解きましょう。
点と直線の距離については既に学んでいると思いますが、以下の公式によって距離\(d\)を得ることができます。
- \(d=\displaystyle\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}\)
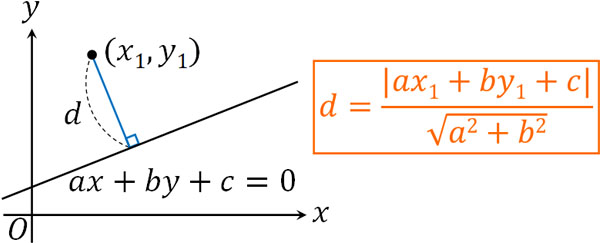
それでは、以下の問題を解きましょう。
- 直線\(y=x+2\)について、円\(x^2+y^2=5\)の内部に存在する弦(直線)の長さを求めましょう。
\(y=x+2\)は\(x-y+2=0\)に変形できます。また円の中心は\((0,0)\)です。そこで公式を利用して、円の中心と直線の距離\(d\)を計算しましょう。
\(d=\displaystyle\frac{|0-0+2|}{\sqrt{1^2+(-1)^2}}\)
\(d=\sqrt{2}\)
また円の中心をO、円と直線の共有点をそれぞれA、Bとすると、OAの距離は円の半径と同じなので\(\sqrt{5}\)です。
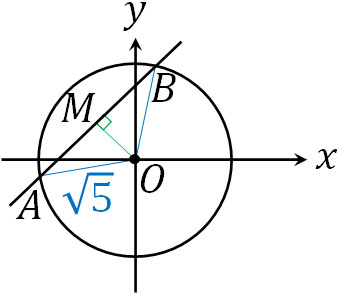
またABの中点をMとすると、三平方の定理より、以下のようにAMの距離を計算できます。
\(AM^2=(\sqrt{5})^2-(\sqrt{2})^2\)
\(AM=\sqrt{3}\)
求める弦(直線)ABの長さはAMの長さの2倍であるため、答えは\(2\sqrt{3}\)と計算できます。
円の接線の方程式と公式
場合によっては、直線は円に接します。それでは、円の接線の方程式を計算なしに得る方法はないのでしょうか。円の接線の方程式については公式が存在します。公式を覚える必要はあるものの、公式を利用すれば、計算なしに円の接線を求めることができます。
円\(x^2+y^2=r^2\)の上に存在する点\((x_1,y_1)\)について、接線の方程式を得る公式は以下になります。
- \(x_1x+y_1y=r^2\)
例えば円\(x^2+y^2=5\)の上に存在する点\((1,2)\)について、接線の方程式は\(x+2y=5\)です。
ただ中心が原点ではない円は多いです。そこで、中心が原点ではない場合に接線の方程式を得る公式を覚えましょう。円\((x-a)^2+(y-b)^2=r^2\)の上に存在する点\((x_1,y_1)\)について、接線の方程式を得る公式は以下になります。
- \((x_1-a)(x-a)+(y_1-b)(y-b)=r^2\)
それでは、以下の問題を解きましょう。
- 円\((x-2)^2+(y-3)^2=25\)について、円の上に存在する点\((5,7)\)を通る接線の方程式を求めましょう。
公式を利用することにより、以下のように計算できます。
\((5-2)(x-2)+(7-3)(y-3)=25\)
\(3x-6+4y-12=25\)
\(3x+4y-43=0\)
こうして、円の接線の方程式は\(3x+4y-43=0\)とわかりました。
円外の点から円に引いた接線の方程式
それでは先ほどの公式を利用して、円外の点から円に向けて引いた接線の方程式を計算しましょう。円の上に存在する点Aの接線ではなく、円外の点Aから円に向けて引いた接線であることに注意しましょう。以下の問題の答えは何でしょうか。
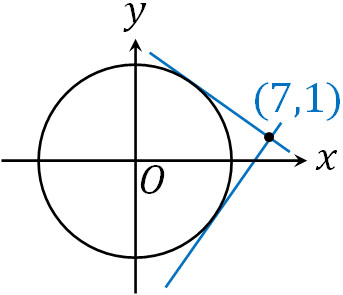
- 点\((7,1)\)から円\(x^2+y^2=25\)に向けて接線を引く場合、接点の座標を求めましょう。
まず、接点を\((a,b)\)としましょう。公式を利用すると、接線の方程式は\(ax+by=25\)となります。直線\(ax+by=25\)は点\((7,1)\)を通るため、\(7a+b=25\)となります。
また接点\((a,b)\)は円上の点であるため、\(a^2+b^2=25\)です。そこで、2つの式を連立させることで答えを得ましょう。\(7a+b=25\)であるため、\(b=-7a+25\)です。そこで、\(b=-7a+25\)を\(a^2+b^2=25\)に代入しましょう。
\(a^2+b^2=25\)
\(a^2+(-7a+25)^2=25\)
\(50a^2-350a+600=0\)
\(a^2-7a+12=0\)
\((a-3)(a-4)=0\)
\(a=3,4\)
\(a=3\)のとき、\(b=4\)です。また\(a=4\)のとき、\(b=-3\)です。そのため、答えは\((3,4)\)と\((4,-3)\)です。
こうして、2つの答えを得ることができました。なお接線の方程式を得たい場合、座標を利用して計算しましょう。
ちなみにこの問題について、中心と直線の距離を利用することによっても答えを得ることができます。さらには、重解をもつと考え、判別式が\(D=0\)となる性質を利用することによっても答えを計算できます。複数の計算方法があるため、すべての方法によって計算できることが望ましいです。
円と直線の関係を利用して距離を計算する
円と直線について、方程式を連立させることによって交点の座標を得ることができます。座標を知る必要がなく、円と直線の位置関係を知りたい場合、判別式を利用することによって共有点の数を知れます。また判別式を利用しなくても、円の半径\(r\)と円と直線の距離\(d\)を確認することによっても、交点の数がわかります。
点と直線の距離を計算するとき、公式を利用しましょう。円と直線の関係では、点と直線の距離を計算できるようになる必要があります。
また、円の接線の方程式を得る公式を覚えましょう。公式を利用することにより、計算なしに接線の方程式を得ることができます。
判別式や点と直線の距離など、円と直線の関係では、これまで学んだ内容を利用します。それに加えて、円の接線の方程式を得る公式を覚えるといいです。