数列で学ぶ内容に漸化式があります。多くの人が苦手とする内容が漸化式です。漸化式は解き方が決まっています。そのため、答えを得られるかどうかというのは、問題の解き方を知っているかどうかにかかっています。
漸化式の中でも、基本的な内容に等差数列、等比数列、階差数列が関わる漸化式があります。漸化式の応用問題というのは、これら基本的な数列の内容を利用して計算しなければいけません。
つまり、漸化式で等差数列、等比数列、階差数列を理解していないと、漸化式の問題を解くことができません。そのため、必ず解き方を覚えましょう。
それでは、漸化式の基本である等差数列、等比数列、階差数列はどのような内容なのでしょうか。漸化式の基本を解説していきます。
もくじ
以前の結果を利用して計算する漸化式
まず、漸化式とは何でしょうか。漸化式とは、以前の結果を利用することによって新たな結果を得られる式を指します。
例えば、毎月おこづかいを3000円もらえるとします。この場合、一か月が経過するごとに3000円ずつ貯金が増えます。つまり、いまの貯金額\(a_n\)に対して3000円を足すと、来月の貯金額\(a_{n+1}\)になります。
- \(a_{n+1}=a_n+3000\)
また再来月の貯金額\(a_{n+2}\)については、来月の貯金額\(a_{n+1}\)を利用することで計算できます。
- \(a_{n+2}=a_{n+1}+3000\)
このように、以前の結果を利用することによって次の結果を得ることができます。これが漸化式です。
漸化式の基本を学ぶ
漸化式で最も基本的な内容が等差数列、等比数列、階差数列です。公差を\(d\)、公比を\(r\)、数列の一般項を\(f(n)\)とすると、それぞれ以下のようになります。
- 等差数列型:\(a_{n+1}-a_n=d\)
- 等比数列型:\(a_{n+1}=ra_n\)
- 階差数列型:\(a_{n+1}-a_n=f(n)\)
これらの公式を覚える必要はありません。数列の性質を理解していれば、この公式になるのは当然だからです。それでは、それぞれの漸化式を確認していきましょう。
等差数列を利用する漸化式の計算
まず、等差数列の漸化式を確認しましょう。公差\(d\)が同じである場合、その数列は等差数列です。以下のように、公差\(d\)ずつ増えていきます。

これが等差数列の性質であるため、両隣の項の差は必ず公差\(d\)になります。そのため、以下の公式が成り立ちます。
- \(a_{n+1}-a_n=d\)
この性質を利用して、等差数列の漸化式を解きましょう。以下の問題の答えは何でしょうか。
- \(a_1=5\)、\(a_{n+1}-a_n-2=0\)のとき、数列の一般式\(a_n\)を求めましょう。
\(a_{n+1}-a_n-2=0\)より、\(a_{n+1}-a_n=2\)であるため、公差は2です。つまり、この数列は初項5、公差2の等差数列です。そのため、以下の式になります。
\(a_n=5+(n-1)2\)
\(a_n=2n+3\)
こうして、漸化式を利用することによって等差数列の一般式を得ることができました。
等比数列での漸化式と計算
同様に考えて、等比数列の漸化式に関する問題を解けるようになりましょう。公比が\(r\)の場合、等比数列では以下のように必ず\(r\)の掛け算になります。
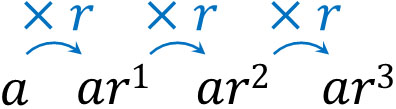
そのため\(a_n\)に対して\(r\)をかけると、\(a_{n+1}\)になります。つまり、以下の公式を作れます。
- \(a_{n+1}=ra_n\)
それでは、以下の問題の答えは何でしょうか。
- \(a_1=3\)、\(a_{n+1}+2a_n=0\)のとき、数列の一般式\(a_n\)を求めましょう。
以下のように計算しましょう。
\(a_{n+1}+2a_n=0\)
\(a_{n+1}=-2a_n\)
こうして初項3、公比\(-2\)の等比数列とわかります。そのため、一般式は以下のようになります。
\(a_n=3·(-2)^{n-1}\)
公比数列の漸化式を利用することにより、一般項を得ることができました。
式\(f(n)\)を含む場合、階差数列を利用する
2つの項を利用して差を計算するとき、式\(f(n)\)が含まれることもあります。2つの項の差によって得られる式というのは、階差数列の一般項を指します。階差数列を学ぶとき、階差数列の一般項\(b_n\)は以下の計算によって得られるとすでに学んでいると思います。
- \(b_n=a_{n+1}-a_n\)
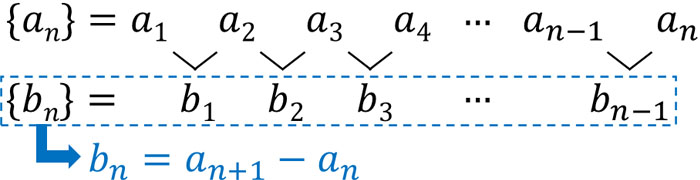
漸化式の計算では、階差数列の一般項を\(b_n\)ではなく、\(f(n)\)と表しましょう。そうすると、以下の公式を得ることができます。
- \(a_{n+1}-a_n=f(n)\)
階差数列の性質を理解していれば、なぜこの公式を得られるのか容易にわかります。なお階差数列ですでに学んでいる通り、以下が階差数列を利用して一般項を得られる公式です。
- \(a_n=a_1+\displaystyle\sum_{k=1}^{n-1}{b_k}\)
- ※\(n≧2\)のとき
\(b_n\)を\(f(n)\)に変えると、以下の表記になります。
- \(a_n=a_1+\displaystyle\sum_{k=1}^{n-1}{f(k)}\)
- ※\(n≧2\)のとき
そこで、この公式を利用することで一般項を計算しましょう。以下の問題の答えは何でしょうか。
- \(a_1=4\)、\(a_{n+1}=a_n+2n+1\)のとき、数列の一般式\(a_n\)を求めましょう。
\(a_{n+1}-a_n=2n+1\)であるため、階差数列の一般項は\(2n+1\)です。そこで、階差数列の公式を利用することで元の数列の一般項を計算しましょう。
\(a_n=4+\displaystyle\sum_{k=1}^{n-1}{(2k+1)}\)
\(a_n=4+2·\displaystyle\frac{1}{2}(n-1)n\)\(+(n-1)\)
\(a_n=n^2+3\)
なお\(n=1\)のとき、\(a_1=4\)です。\(a_1\)のときも成り立つため、\(a_n=n^2+3\)です。こうして、一般式を得ることができました。階差数列を理解しているのであれば、漸化式に階差数列の一般式が含まれる場合であっても、計算は難しくありません。
漸化式の解き方を覚えるべき
数学で漸化式は難しい内容の一つです。そのため多くの人が苦手としますが、漸化式では等差数列、等比数列、階差数列を利用して計算することになります。
ここまで解説した内容は難しくなく、等差数列や等比数列、階差数列を利用することで一般項を得ることができます。そこで、漸化式の意味や公式が成り立つ理由を学びましょう。そうすれば、応用問題を解けるようになります。
ただ、基本を理解していないと漸化式の問題を解くことができません。そこで公式を暗記するのではなく、なぜ公式が成り立つのか理解しましょう。
基本を学ぶことにより、応用問題を解けるようになります。そこで等差数列、等比数列、階差数列の漸化式を解けるようになりましょう。






