数列には複数の種類があります。最も重要な数列は等差数列と等比数列です。ただ、これらの数列を知っていても解けない問題は多いです。
特殊な数列には複数の種類があり、その一つに階差数列があります。一見すると規則性のない数列であるものの、2つの項の差を利用することにより、規則性を得ることができます。このとき項数と初項に気を付けて計算しなければいけません。
解き方を理解していないと、階差数列の答えを得るのは難しいです。また場合によっては、階差数列を2回利用しなければいけないこともあります。
それでは、どのように階差数列に関する問題を解けばいいのでしょうか。階差数列の概要や公式、一般項の計算方法を解説していきます。
もくじ
階差数列では両隣にある2つの項の引き算をする
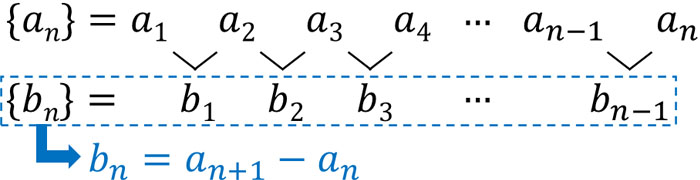
一見すると、規則性のない数列が階差数列です。階差数列では、隣り合う2つの項の差を計算します。そこで数列\(\{a_n\}\)について、階差数列を\(\{b_n\}\)とするとき、以下のように階差数列を表すことができます。
- \(b_n=a_{n+1}-a_n\)
例えば、以下の数列はどのように考えればいいでしょうか。
- \(4,7,12,19,28…\)
そこで、以下のように階差数列を作りましょう。
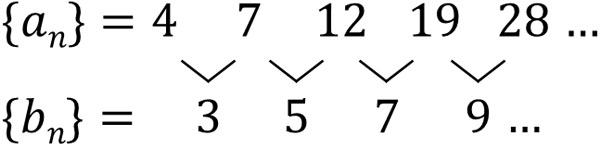
このように確認すると、階差数列は初項3、公差2の等差数列とわかります。そのため、以下のように階差数列の一般項を得ることができます。
\(b_n=3+(n-1)2\)
\(b_n=2n+1\)
こうして、階差数列の一般項\(b_n\)を計算できました。
階差数列を利用して一般項\(a_n\)を得る公式
それでは、階差数列の一般項\(b_n\)を利用して\(a_n\)を得るにはどうすればいいのでしょうか。階差数列を利用して\(a_n\)を計算するとき、利用する公式は以下になります。
\(a_n=a_1+(b_1+b_2+…+b_{n-1})\)
\(a_n=a_1+\displaystyle\sum_{k=1}^{n-1}{b_k}\)
※\(n≧2\)のとき
証明方法は簡単であり、数列\(\{a_n\}\)と階差数列\(\{b_n\}\)を以下のように表し、足し算をしましょう。
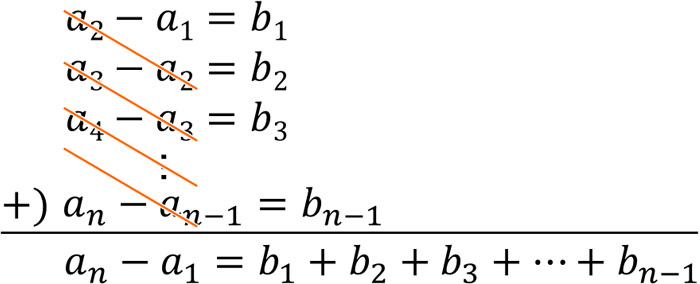
こうして、先ほど記した公式を得ることができます。
\(a_n-a_1=(b_1+b_2+…+b_{n-1})\)
\(a_n=a_1+(b_1+b_2+…+b_{n-1})\)
\(a_n=a_1+\displaystyle\sum_{k=1}^{n-1}{b_k}\)
階差数列の公式は覚えましょう。
項数に注意して計算し、初項を確認する
なお足し算をするとき、\(b_k\)の項数は\(n\)ではなく、\(n-1\)までの項数を足すことに注意しましょう。先ほどの公式を確認すると、\(a_n=a_1+\displaystyle\sum_{k=1}^{\color{red}{n-1}}{b_k}\)となっており、これは\(k=1\)から\(k=n-1\)までの和を意味します。
もう一つの注意点として、\(n≧2\)であり、\(n=1\)を含みません。先ほど説明した通り、シグマの計算は\(k=1\)から\(k=n-1\)までの和であり、\(n=1\)だと計算できません。そのため、\(n=1\)が成り立つかどうかは別途確認しなければいけません。
階差数列というのは、先ほど解説した通り、2つの項の差を利用します。項が一つでは階差を得ることができないため、\(n=1\)の場合と\(n≧2\)の場合を分けて考える必要があります。
それでは先ほど記した以下の数列について、\(a_n\)の一般項を求めましょう。
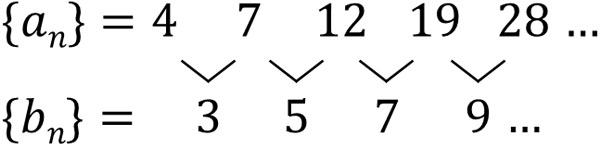
前述の通り、階差数列の一般項は\(b_n=2n+1\)です。そこで、以下のように\(a_n\)を計算します。
\(a_n=4+\displaystyle\sum_{k=1}^{n-1}{(2k+1)}\)
\(a_n=4+2\displaystyle\sum_{k=1}^{n-1}{k}\)\(+\displaystyle\sum_{k=1}^{n-1}{1}\)
\(a_n=4+2·\displaystyle\frac{1}{2}(n-1)n+(n-1)\)
\(a_n=n^2+3\)
こうして\(n≧2\)のとき、\(a_n=n^2+3\)とわかりました。なお\(n=1\)のとき、\(a_1=4\)であるため、この一般項は\(n=1\)のときも成り立ちます。そのため、\(a_n=n^2+3\)です。
\(n=1\)のときも一般項が成り立つかどうか確認しなければ、すべての自然数\(n\)について、一般項\(a_n\)が成り立つかどうかわかりません。そのため階差数列では、この確認が必要です。
第2階差数列を利用して一般項を得る
なお階差数列の計算では、階差数列を2回利用することで一般項\(a_n\)を得られるケースもあります。そのため一回目の階差数列\(b_n\)で規則性を得られない場合、さらに階差数列を確認しましょう。この階差数列\(c_n\)を第2階差数列といいます。
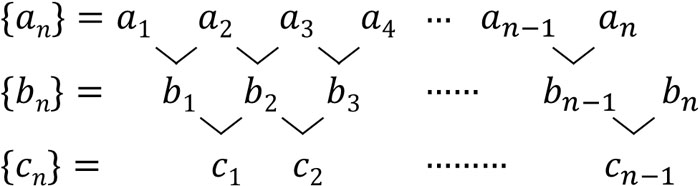
第2階差数列\(c_n\)を利用して一般項を得る方法はこれまで解説した公式と同じであり、以下の公式を利用します。
- \(b_n=b_1+\displaystyle\sum_{k=1}^{n-1}{c_k}\)
※\(n≧2\)のとき
階差数列であるため、項数は\(n-1\)になります。また\(n≧2\)のときに成り立つ公式であるため、\(n=1\)のときの確認を必ず行わなければいけません。
第2階差数列の練習問題
それでは、第2階差数列の練習問題を解きましょう。以下の数列の一般項\(\{a_n\}\)を求めましょう。
- \(0,6,24,60,120,210…\)
階差数列\(\{b_n\}\)と第2階差数列\(\{c_n\}\)を計算すると、以下のようになります。
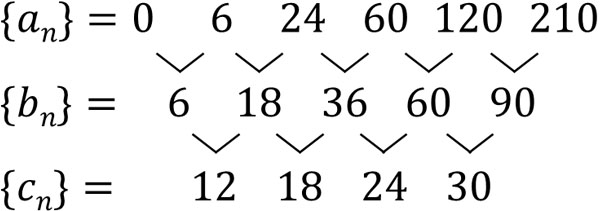
第2階差数列\(\{c_n\}\)は初項12、公差6の等差数列です。そのため、一般項は以下のようになります。
\(c_n=12+(n-1)6\)
\(c_n=6n+6\)
次に、階差数列\(\{b_n\}\)の一般項を計算しましょう。
\(b_n=6+\displaystyle\sum_{k=1}^{n-1}{(6k+6)}\)
\(b_n=6+6·\displaystyle\frac{1}{2}(n-1)n\)\(+6(n-1)\)
\(b_n=3n^2+3n\)
\(n=1\)を代入すると\(b_1=6\)であり、\(n=1\)のときも成り立ちます。そのため、一般項は\(b_n=3n^2+3n\)です。そこで\(b_n\)を利用して\(a_n\)を計算しましょう。
\(a_n=0+\displaystyle\sum_{k=1}^{n-1}{(3k^2+3k)}\)
\(a_n=3·\displaystyle\frac{1}{6}(n-1)n(2n-1)\)\(+3·\displaystyle\frac{1}{2}(n-1)n\)
\(a_n=\displaystyle\frac{1}{2}(n-1)n(2n-1)\)\(+\displaystyle\frac{3}{2}(n-1)n\)
\(a_n=\displaystyle\frac{1}{2}(n-1)n(2n-1+3)\)
\(a_n=\displaystyle\frac{1}{2}(n-1)n(2n+2)\)
\(a_n=(n-1)n(n+1)\)
\(n=1\)を代入すると\(a_1=0\)であり、\(n=1\)のときも成り立ちます。そのため、一般項は\(a_n=(n-1)n(n+1)\)です。こうして、第2階差数列を利用することで一般項\(a_n\)を得ることができました。
階差数列を用いて一般項を得る
数列を確認して規則性を確認できない場合、階差数列を利用しましょう。2つの項の差を確認することにより、規則性を見つけられるケースがあります。場合によっては、2回の階差を利用することで規則性を得られるケースもあります。
階差数列を用いて一般項を計算するとき、公式を利用しましょう。このとき、項数が\(n-1\)になることに注意が必要です。
また、階差数列の公式が成り立つのは\(n≧2\)のときです。そこで、\(n=1\)のときも成り立つかどうか必ず確認しましょう。\(n≧2\)を考慮せずに階差数列の公式を利用して計算する場合、それは間違いになります。
階差数列を利用して計算をするとき、独自の注意点があります。これらを把握し、公式を活用して一般項を計算しましょう。