すべての人が経験したことのある自然現象にドップラー効果があります。救急車が大きな音で近づいてくるとき、あなたに向かってくるときの音は高いものの、あなたから遠ざかるときの音は低くなります。この現象がドップラー効果です。
なぜ、ドップラー効果が起こるのでしょうか。音は波の一種であるため、物理で波動を学ぶことによってドップラー効果を理解できます。
なおドップラー効果には複数の種類があります。音源があなたに近づくケースがあれば、あなたが音源に近づくケースもあります。場合によっては、音源(またはあなた)が斜めに移動することもあります。風が吹いている場面も想定できます。
これらの場面について、振動数の計算を行えるようにしましょう。そこで、ドップラー効果の概念や公式の意味、計算方法を解説していきます。
もくじ
移動によって振動数が変化するドップラー効果の概要
救急車のサイレンはドップラー効果の例としてひんぱんに利用されます。それでは、救急車の音が高くなったり低くなったりするのはなぜなのでしょうか。
ドップラー効果を学ぶとき、「振動数が多いと音が高くなる」という事実を覚えましょう。ドップラー効果に関する問題を解くとき、この事実が役に立ちます。
例えば、糸(弦)を引っ張って音をならす場面をイメージしましょう。このとき、糸を強く引っ張ったほうが高い音を生じるのは容易に想像できると思います。
張力が強い場合、糸を弾いたときに元の状態に戻る力が強いため、結果として素早く振動します。言い換えると、振動数(1秒間に振動する回数)が多くなります。振動数が多いと、高い音になるのです。
・移動すると振動数が変化する
また物体が移動すると、振動数が変化します。音源と音を聞く人が両方とも静止している場合、音は音速で移動します。音波は空気を伝わるため、音の速度が変化することはありません。そのため静止している場合、音は同心円状に広がります。
一方、音源またはあなたが移動する場合は振動数が変化します。例えば音源(救急車)が移動する場面を考えましょう。音速は変化しないものの、救急車があなたに向かって移動している場合、救急車があなたに近づいた分だけ、あなたは多くの波を聞くことになります。
通常よりも聞き取る波の数が多いというのは、振動数(1秒間に振動する回数=1秒間にあなたが聞き取る波の数)が増えることを意味します。言い換えると、音が高くなります。
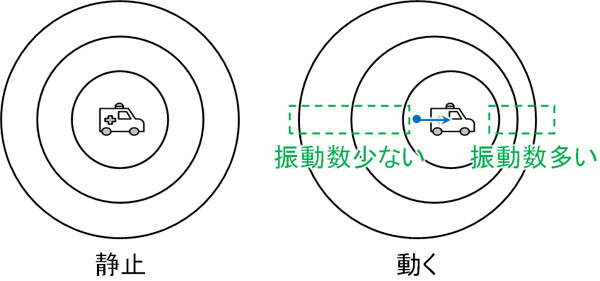
一方、救急車が遠ざかる場合、音源が遠ざかる分だけあなたが聞き取れる波の数は少なくなります。つまり振動数が少なくなり、結果として音が低くなります。これがドップラー効果の概要です。
音源が動く場合のドップラー効果:波長\(λ\)の変化
それでは、ドップラー効果が起こるときの振動数を計算できるようになりましょう。公式を暗記しても意味がないため、公式を作れるようにしましょう。そうすれば、応用問題が出されても問題を解けるようになります。
音源の振動数が\(f\)Hzの場合、あなたは1秒間に\(f\)回の波を聞き取ることになります(音源とあなたが静止している場合)。このとき基準となるのが音速です。前述の通り、音速が変化することはありません。空気を伝わる音の速度は常に一定です。
そこで、音速を\(V\)m/sとします。前述の通り、1秒間に存在する波の数が振動数\(f\)です。そのため1秒間には、\(V\)mの間に\(f\)個の波が存在することになります。言い換えると、あなたは\(V\)mの間に存在する\(f\)個の波を1秒で聞くことになります。
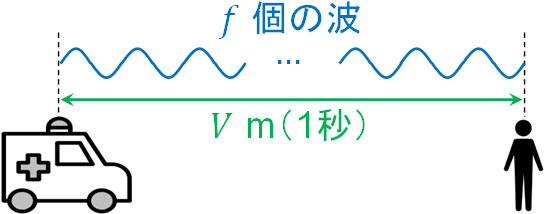
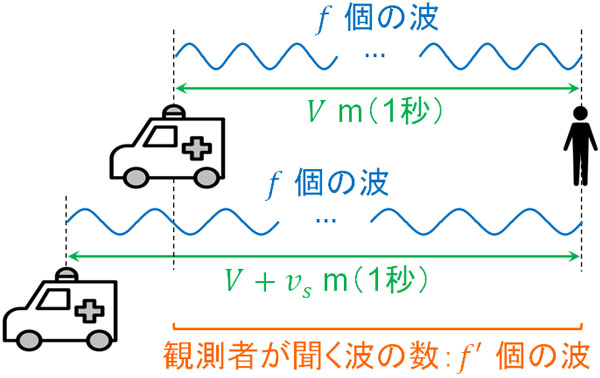
それでは、音源(救急車)があなたに向かって速さ\(v_s\)m/sで近づいてくる場合、どのようになるでしょうか。
音源が発する波の数は\(f\)個であり、変化はありません。一方で音源は動いており、1秒後には\(v_s\)mあなたに近づくことになります。この場合、\(V-v_s\)mの間に\(f\)個の波が存在することになります。
\(f\)個の波が\(V\)mの間に存在するのか、それとも\(V-v_s\)mの間に存在するのかが異なります。
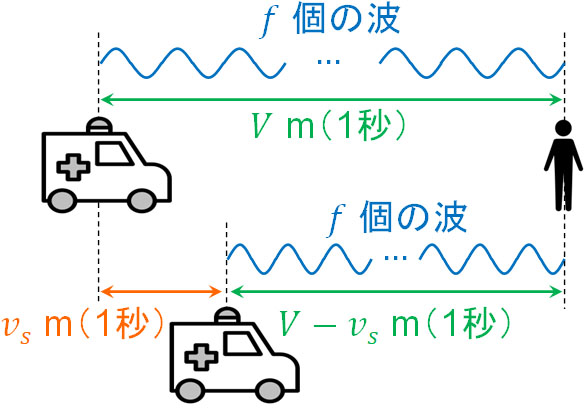
音源が動く場合、短い距離に\(f\)個の波が存在することになるため、その分だけ波長\(λ\)は短くなります。
静止している場合、1秒間に\(f\)個の波が存在し、1個の波の長さ(波長)は\(λ\)です。そのため、音速\(V\)を用いて以下のように表すことができます。
- \(V=fλ\)
つまり、\(λ=\displaystyle\frac{V}{f}\)となります。
一方、音源が移動している場合はどうでしょうか。この場合、1秒間では\(V-v_s\)mの間に、1個の長さ(波長)が\(λ’\)である波が\(f\)個存在することになります。そのため、以下の式を作れます。
- \(V-v_s=fλ’\)
つまり、\(λ’=\displaystyle\frac{V-v_s}{f}\)です。音源があなたに向かってくる場合、短い距離の間に多くの波が存在することになるため、波長が圧縮されて短くなるのは容易に想像できると思います。
・音の速さ\(V\)は変わらない
参考までに、音源が速さ\(v_s\)で動いても音の速さ\(V\)は変わりません。つまり、音の速さが\(V+v_s\)になることはありません。音は空気によって伝わり、空気に伝わった瞬間に音源の影響を受けなくなるからです。
ベルトコンベアーを想像すると、理由を理解しやすいです。音は常に一定の速さで波を運んでいるベルトコンベアーです。ベルトコンベアーが速さ\(V\)で物を運ぶとします。あなたが止まっている状態で物をベルトコンベアーに乗せると、速さ\(V\)で物が運ばれます。
それでは、あなたが速さ\(v_s\)で走りながらベルトコンベアーに物を置く場合、物の速さはどうなるでしょうか。ベルトコンベアーは一定の速さ\(V\)で物を運ぶため、あなたが静止している状態で物を置いても、走っている状態で物を置いても、ベルトコンベアーが物を運ぶ速度は\(V\)です。
観測者が感じる振動数\(f’\)を得る
次に、観測者を中心に考えて振動数の計算をしましょう。両者が静止している場合、前述の通り観測者は1秒で\(V\)m分の波を聞きます。また音源が動いている場合であっても、観測者は動いていないため、同様に1秒で\(V\)m分の波を聞きます。
このとき、音源は速さ\(v_s\)m/sで観測者に近づきながら動いているため、その分だけ波長\(λ\)が短くなっており、波長は\(λ’\)になっています。つまり、音源が動いて観測者が静止している場合、観測者は多くの波を聞くことになります。
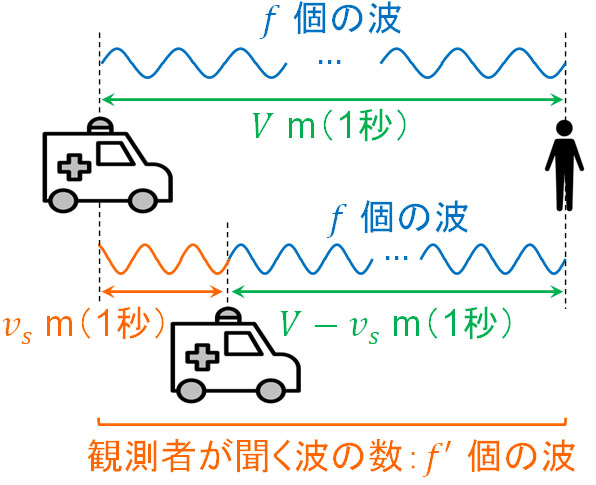
それでは、音源が発する振動数\(f\)ではなく、観測者が聞く波の振動数\(f’\)はどのように計算すればいいのでしょうか。言い換えると、観測者が1秒間に聞く波の数\(f’\)はいくらでしょうか。
音源があなたに近づいているとき、一つの波の長さは\(λ’\)であり、1秒に\(f’\)個の波があります。そのため\(λ’×f’\)により、音速\(V\)と等しくなります。つまり、波の公式でひんぱんに利用される以下の公式を利用しましょう。
- \(V=λ’f’\)
なお、先ほど解説した通り\(λ’=\displaystyle\frac{V-v_s}{f}\)です。そこで、\(λ’=\displaystyle\frac{V-v}{f}\)を代入しましょう。
\(V=λ’f’\)
\(V=\displaystyle\frac{V-v_s}{f}f’\)
\(Vf=(V-v_s)f’\)
\(f’=\displaystyle\frac{V}{V-v_s}f\)
こうして、音源があなたに近づくときのドップラー効果の公式である\(f’=\displaystyle\frac{V}{V-v_s}f\)を得ることができました。観測者はこの振動数を聞くことになります。
なお分母に音源が近づく速度\(v_s\)があるため、公式を利用して計算すると\(f’\)の値は\(f\)よりも大きくなります。つまり高い音をあなたは聞くことになり、公式は間違っていないとわかります。
音源が遠ざかる場合のドップラー効果
なお音源が近づく場合ではなく、音源が遠ざかるケースもあります。この場合、先ほどの公式を以下のように変えましょう。
- \(f’=\displaystyle\frac{V}{V+v_s}f\)
音源が遠ざかるため、観測者が聞く振動数\(f’\)の値は小さくならなければいけません。そこで、先ほどとは逆に、速さ\(v_s\)で遠ざかる場合は分母に\(v_s\)を足しましょう。
それでは、先ほどと同じように公式を証明しましょう。波の公式より、音速\(V\)、振動数\(f\)、波長\(λ\)の場合、\(V=fλ\)が成り立ちます。
それに対して音源が速さ\(v_s\)で遠ざかる場合、1秒では\(V+v_s\)mの間に\(f\)個の波が存在することになります。そのため、音源が遠ざかる場合の波長を\(λ’\)とすると、以下の関係が成り立ちます。
- \(V+v_s=fλ’\)
長さ\(λ’\)の波が\(f\)個あると、長さは\(V+v_s\)mになります。こうして、\(λ’=\displaystyle\frac{V+v_s}{f}\)になるとわかります。
なお、1秒間に観測者が聞く波は\(V\)m分で共通しています。音源が遠ざかることによる波長が\(λ’\)、振動数が\(f’\)の場合、\(V=f’λ’\)になります。そこで、\(λ’=\displaystyle\frac{V+v_s}{f}\)を代入しましょう。
\(V=f’λ’\)
\(V=\displaystyle\frac{V+v_s}{f}f’\)
\(Vf=(V+v_s)f’\)
\(f’=\displaystyle\frac{V}{V+v_s}f\)
こうして、音源が遠ざかる場合の公式を得ることができました。音源が近づく場合と遠ざかる場合を比較すると、\(v_s\)の前の符号が違うだけです。
符号がマイナスになるのか、それともプラスになるのかについて、音源が近づく場合は振動数の値が大きくなって音が高くなる必要があるため\(v_s\)の符号はマイナスになります。一方、音源が遠ざかる場合は音が低くなり、振動数の値は小さくなる必要があるため、\(v_s\)の符号はプラスになります。
観測者が動く場合のドップラー効果
それでは、観測者が動く場合はどのように考えて計算すればいいのでしょうか。先ほどとは異なり、音源(救急車)を静止させ、あなたが動く場面を考えましょう。
音源とあなたの両方が静止している場合、1秒間であなたが聞く波の数は\(f\)個です。それに対して、あなたが\(v_o\)の速さで音源に向かって走る場面を考えましょう。
この場合、あなたは音源に対して走るため、通常よりも多くの波を聞き取ることになります。静止している状態では、\(V\)mに含まれている波を1秒で聞くことになります。ただあなたは走っているため、\(V+v_o\)mに含まれている波を1秒間で聞くことになります。
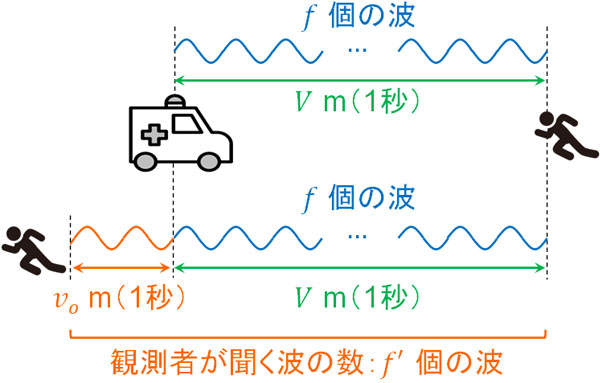
音源は動かないため、波長\(λ\)に変化はありません。ただ相対速度で考えると、音速\(V\)とあなたが走る速度\(v_o\)が組み合わさり、あなたにとって音の相対速度は\(V+v_o\)となります。そこで相対速度\(V+v_o\)を用いると、観測者(あなた)が聞く波の振動数\(f’\)は公式より以下のようになります。
\(V+v_o=f’λ\)
なお前述の通り\(V=fλ\)であり、\(λ=\displaystyle\frac{V}{f}\)です。そこで、\(λ=\displaystyle\frac{V}{f}\)を代入しましょう。
\(V+v_o=f’λ\)
\(V+v_o=\displaystyle\frac{V}{f}f’\)
\(f’=\displaystyle\frac{V+v_o}{V}f\)
こうして、あなたが音源に向かって走るときに聞こえる波の振動数は\(f’=\displaystyle\frac{V+v_o}{V}f\)と計算できます。
観測者が音源に向かって走る場合、多くの波を聞くことになるため、音は高くなります。また公式を確認すると、分子に\(v_o\)を加えることになるため、振動数は大きくなり、音が高くなるとわかります。そのため、公式は間違っていないと判断できます。
・観測者が音源から遠ざかるケース
一方、あなたが音源から遠ざかる場合、先ほどとは逆に考えましょう。音源は静止しており、波長\(λ\)は一定です。しかし、あなたは速さ\(v_o\)で音源から遠ざかっているため、1秒間では\(v_o\)mに含まれている波の数を聞き逃していることになります。つまり、その分だけ振動数は小さくなり、聞こえる音は低くなります。

相対速度で考えると、あなたにとって音の速さは\(V-v_o\)です。波長は\(λ\)であり、観測者が聞く振動数は\(f’\)です。そのため、以下の式を作れます。
\(V-v_o=f’λ\)
そこで、先ほどと同じように\(λ=\displaystyle\frac{V}{f}\)を代入しましょう。
\(V-v_o=f’λ\)
\(V-v_o=\displaystyle\frac{V}{f}f’\)
\(f’=\displaystyle\frac{V-v_o}{V}f\)
こうして、観測者が音源から遠ざかる場合の公式を得ることができました。物理では、公式を暗記しても意味がありません。必ず公式が何を表しているのか学び、公式を導き出せるようにしましょう。
音源と観測者が動く場合のドップラー効果
なお物理でドップラー効果の問題が出されるとき、音源と観測者の両方が動くケースがあります。この場合、2つの公式を組み合わせましょう。音源が速さ\(v_s\)で動き、観測者が速さ\(v_o\)で動く場合、公式は以下になります。
- \(f’=\displaystyle\frac{V±v_o}{V±v_s}f\)
音源が動く場合、先ほどの説明より、分母が変化します。音源があなたに近づく場合、音は高くなり、振動数は大きくならなければいけません。そこで、\(v_s\)を引くことで分母を小さくしましょう。音源が遠ざかる場合、反対に\(v_s\)を足します。
一方、観測者が動く場合、分子が変化します。あなたが音源に向かって走る場合、多くの波を聞くことになり、振動数は大きくなります。そこで、分子に\(v_o\)を足します。あなたが音源から遠ざかる場合、反対に分子から\(v_o\)を引きましょう。
それでは、練習問題を解いてみましょう。以下の問題の答えは何でしょうか。
- 振動数600Hzの音源があり、観測者に向かって速さ40m/sで動いています。一方、観測者は速さ10m/sで音源に向かって動いています。音速を340m/sとするとき、観測者が感じる振動数を計算しましょう。
音源は観測者に向かって動いているため、振動数は大きくなり、音は高くなります。また観測者は音源に向かって動いているため、同様に振動数は大きく、音は高くなります。そこで分母では引き算を行い、分子では足し算をしましょう。
\(f=\displaystyle\frac{340+10}{340-40}×600\)
\(=700\)
こうして、観測者には700Hzの音が聞こえるとわかります。
斜めに動く場合のドップラー効果は角度を考慮する
ここまで、ドップラー効果の基本を解説してきました。次に、音源または観測者が斜めに動く場合のドップラー効果を確認していきましょう。
力学では、斜めに働く力は角度を利用します。つまり、sinθまたはcosθを利用してそれぞれのベクトルに分解して計算します。同様に、ドップラー効果でも角度を利用してベクトルに分解しましょう。
・音源が近づく場合
斜めの状態では、直線状態ではないので速度をそのまま利用することはできません。そのため、角度を利用しましょう。考え方は難しくなく、力学の問題を解くことができる場合、ドップラー効果の問題を解くのは容易です。
下図のように、音源と観測者との角度をθとします。速さ\(v_s\)で動くとき、観測者に対して速さ\(v_scosθ\)のスピードで移動していることになります。
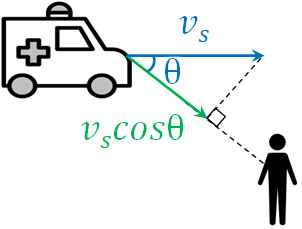
そのため音源が観測者に斜めで近づく場合、公式を以下のように変形しましょう。
- \(f’=\displaystyle\frac{V}{V-v_scosθ}f\)
角度を考慮するだけなので、理解するのは難しくありません。なお音源が観測者から遠ざかる場合、利用する公式は\(f’=\displaystyle\frac{V}{V+v_scosθ}f\)となります。
・観測者が斜めに動く場合
それでは、下図のように観測者が斜めに動く場合はどのように考えればいいのでしょうか。この場合、先ほどと同様に角度を利用してベクトルを分解しましょう。
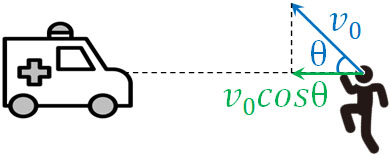
このように考えると、観測者が斜めに動く場合は以下の公式に変化するとわかります。
- \(f’=\displaystyle\frac{V+v_ocosθ}{V}f\)
一方、観測者が音源から遠ざかる場合、公式は\(f’=\displaystyle\frac{V-v_ocosθ}{V}f\)となります。いずれにしても、角度を利用することによって振動数を計算しましょう。
風がある場合のドップラー効果
次に、風がある場合のドップラー効果を解説します。前述の通り、音は空気を伝わります。音が空気を伝わる速度は一定です。
ただ風があると、風によって空気が移動します。つまり音に対して追い風があると、空気が観測者に向かって移動するため、その分だけ音の相対速度が速くなります。一方で音に対して向かい風があると、空気が音源とは反対向きに移動し、結果として音の相対速度は遅くなります。
そこで、音源と観測者の両方が静止している場面を考えましょう。音の速さを\(V\)、風の速さを\(w\)とすると、追い風のときは音の相対速度が速くなり、音が空気を伝わる速さは\(V+w\)となります。一方、向かい風のときは音の相対速度が遅くなり、音が空気を伝わる速さは\(V-w\)となります。
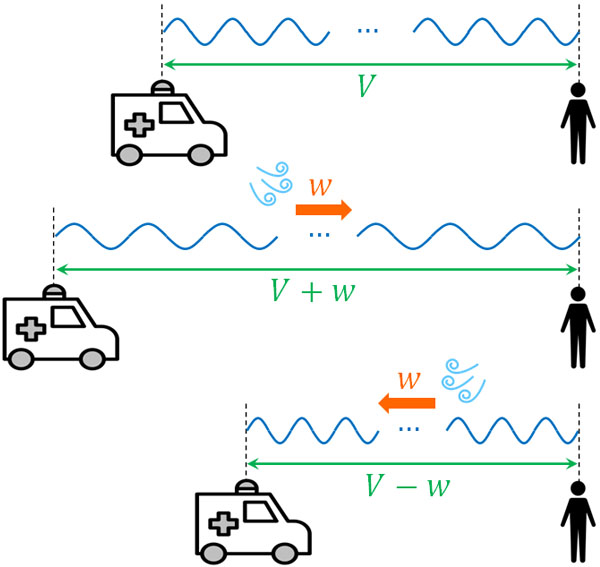
つまり風があると、観測者にとって音の速度が変化します。ここまで、音速は必ず\(V\)であると解説してきました。ただ、これは風がない場合に限られます。風がある場合、\(V\)を\(V+w\)または\(V-w\)に変えましょう。
先ほど説明した通り、ドップラー効果の公式は以下になります。
- \(f’=\displaystyle\frac{V±v_o}{V±v_s}f\)
そこで、この公式を以下のように変形しましょう。
- 音源に対して追い風がある:\(f’=\displaystyle\frac{V+w±v_o}{V+w±v_s}f\)
- 音源に対して向かい風がある:\(f’=\displaystyle\frac{V-w±v_o}{V-w±v_s}f\)
音の速さが\(V\)から\(V+w\)または\(V-w\)に変化することを学べば、風がある場合であってもドップラー効果の計算問題を解くことができます。
ドップラー効果を利用する物理の応用問題
それでは、ここまで解説した知識を利用して練習問題を解いてみましょう。以下の問題の答えは何でしょうか。
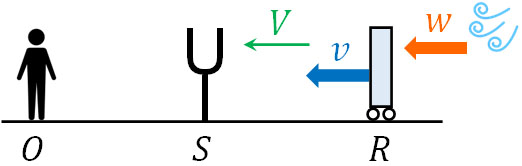
- 観測者O、振動数\(f\)の音源S、反射板Rが一直線上に並んでいます。観測者Oと音源Sは静止しており、反射板Rは速さ\(v\)で左向きに動いています。なお、音速は\(V\)とします。
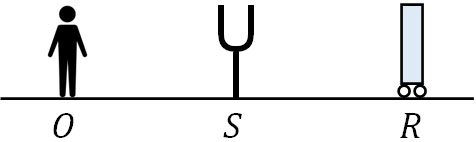
- 観測者が聞く反射音の振動数を求めましょう。
- 風が一定の速さ\(w\)で左向きに吹いているとき、観測者が聞く反射音の振動数を求めましょう。
1) 観測者が聞く反射音の振動数を求めましょう
まず、反射板Rに観測者がいると仮定して、反射板Rの振動数を計算しましょう。
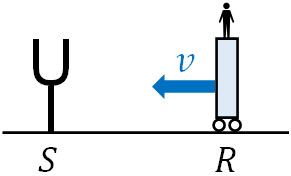
音速が\(V\)であり、反射板Rは速度\(v\)で音源に向かって動いているため、音は高くなります。言い換えると、振動数は大きくなります。そのため、反射板の振動数\(f_R\)は以下のようになります。
\(f_R=\displaystyle\frac{V+v}{V}f\)
こうして、反射板は振動数\(f_R=\displaystyle\frac{V+v}{V}f\)の音を観測者Oに向かって反射する(発している)とわかります。つまり観測者Oにとって反射板は音源です。また音源(反射板)は速度\(v\)で近づくため、通常よりも高い音が聞こえます。つまり、振動数は高くなります。
音源が\(f_R=\displaystyle\frac{V+v}{V}f\)となる振動数を発しており、速度\(v\)で近づく場合、観測者Oが聞く振動数\(f_O\)は以下になります。
\(f_O=\displaystyle\frac{V}{V-v}f_R\)
\(f_O=\displaystyle\frac{V}{V-v}×\displaystyle\frac{V+v}{V}f\)
\(f_O=\displaystyle\frac{V+v}{V-v}f\)
こうして、観測者は振動数\(f_O=\displaystyle\frac{V+v}{V-v}f\)となる反射音を聞くことになるとわかります。
2) 風が一定の速さ\(w\)で左向きに吹いているとき、観測者が聞く反射音の振動数を求めましょう
風が吹いている場合、速さ\(V\)が\(V+w\)または\(V-w\)になります。風は左向きに吹いているため、反射板で聞こえる音というのは、その分だけ音の相対速度が低くなります。つまり、音の速度は\(V-w\)になります。そのため、反射板での振動数は以下になります。
\(f_R=\displaystyle\frac{V-w+v}{V-w}f\)
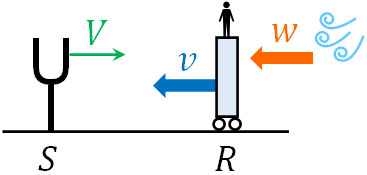
一方、観測者Oが反射板からの音を聞く場合、音の相対速度は速くなります。音の速度は\(V+w\)となるのです。
反射板による振動数は\(f_R=\displaystyle\frac{V-w+v}{V-w}f\)です。また音の速さは\(V\)の代わりに、\(V+w\)となります。そこで、以下の式を作りましょう。
\(f_O=\displaystyle\frac{V+w}{V+w-v}f_R\)
\(f_O=\displaystyle\frac{V+w}{V+w-v}×\displaystyle\frac{V-w+v}{V-w}f\)
こうして、観測者Oが聞く反射音の振動数は\(f_O=\displaystyle\frac{V+w}{V+w-v}·\displaystyle\frac{V-w+v}{V-w}f\)と計算できました。
ドップラー効果による振動数の変化を学ぶ
すべての人にとって、ドップラー効果は身近です。音は波の一種であり、音源や観測者が移動することによって振動数が変化します。つまり、音が高くなったり低くなったりします。
そこで、振動数の変化を計算できるようになりましょう。このとき計算式において、動いている物体の速さの符号がプラスになるのか、それともマイナスになるのかについては、実際に物体が動いている場面を想像しましょう。そうすれば、分母(または分子)の値を大きくすればいいのか、それとも小さくすればいいのかわかります。
またドップラー効果では、斜めに移動したり、風が吹いている場面を想定したりするケースもあります。この場合は角度を利用したり、相対速度を用いたりして計算しましょう。
ドップラー効果に関する物理の問題を解くコツは「問題文にある現象が起こることで、音が高くなるのか、それとも低くなるのか」を確認することです。これによって計算式の符号が確定します。その後、式を作って答えを得ましょう。






