直線のベクトル方程式：交点の位置ベクトル、法線ベクトル

位置ベクトルを利用することにより、直線を表すことができます。位置ベクトルによって点を表現できますが、多くの点が集まることによって直線になるのです。これを直線のベクトル方程式といいます。

数学では、関数を利用することによって特定の直線を表現できます。ただベクトル方程式では、私たちがこれまで学んだ関数とは表記法が異なります。そこで、どのように直線を表せばいいのか学ばなければいけません。

なおベクトルが関わる問題では、交点の位置ベクトルがひんぱんに出題されます。この問題を解くには、ベクトル方程式を用いなければいけません。またベクトル方程式には、法線ベクトル（特定の線に対して垂直のベクトル）も含まれます。

それでは、ベクトルを用いてどのように直線を表現すればいいのでしょうか。直線のベクトル方程式に関する公式や問題の解き方を解説していきます。

1 定点を通り、特定のベクトルに平行な直線
- 1.1 2点を通る直線のベクトル方程式
  - 1.1.1 交点の位置ベクトルの計算方法
- 1.2 定点を通り、特定のベクトルに垂直の直線：法線ベクトル
2 ベクトル方程式を利用して直線を表現する

定点を通り、特定のベクトルに平行な直線

関数によって直線を表すとき、直線の方程式は以下になります。

\(y=ax+b\)

いわゆる一次方程式であり、これによって直線を表現できることは容易に理解できます。それでは、直線をベクトルで表すにはどのようにすればいいのでしょうか。ベクトルを利用する場合、直線の表現方法は複数あります。

まず、「定点を通り、特定のベクトルに平行な直線」を確認しましょう。位置ベクトルは原点Oが始点です。また座標と同じように、特定の点を表すのが位置ベクトルです。そのため\(\overrightarrow{a}=(a_1,a_2)\)の位置ベクトルは座標上の\((a_1,a_2)\)を表します。例えば\(\overrightarrow{a}=(4,3)\)は以下のようになります。

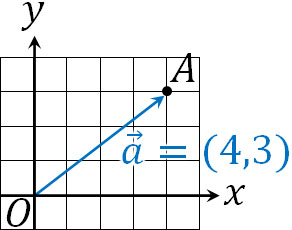
それでは定点A（\(\overrightarrow{a}\)）を通り、\(\overrightarrow{0}\)ではない\(\overrightarrow{d}\)に平行な位置ベクトル\(\overrightarrow{p}\)はどのように表現すればいいでしょうか。先に公式を記すと以下になります。

\(\overrightarrow{p}=\overrightarrow{a}+t\overrightarrow{d}\)

※\(t\)は実数の変数

\(\overrightarrow{a}\)は位置ベクトルであるため、必ずこの点を通ることになります。一方で\(\overrightarrow{d}\)は特定の大きさと向きをもつベクトルです（位置ベクトルではない）。そのため\(\overrightarrow{d}\)を\(t\)倍することにより、特定の点P（\(\overrightarrow{p}\)）を表せます。

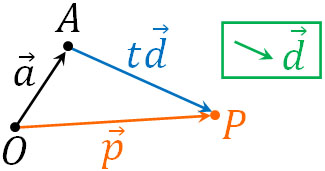
上図より、\(\overrightarrow{p}=\overrightarrow{a}+t\overrightarrow{d}\)となるのは問題なく理解できると思います。

なお\(\overrightarrow{p}\)は位置ベクトルであるため、大きさと方向をもちますが、前述のとおり特定の点を表すことができます。そこで、\(t=-1,0,1,2…\)と代入してみましょう。そうすると、「\(\overrightarrow{p}\)によって描ける点」をつなぐことで直線となります。

このように\(\overrightarrow{p}\)が点であることに着目すると、ベクトル方程式を利用することによって直線を表現できます。なお、\(\overrightarrow{d}\)を直線の方向ベクトル、\(t\)を媒介変数といいます。

それでは、先ほどの公式を利用して問題を解きましょう。以下の問題の答えは何でしょうか。

3点A（\(\overrightarrow{a}\)）、B（\(\overrightarrow{b}\)）、C（\(\overrightarrow{c}\)）が頂点の△ABCについて、辺ACを1:3に内分する点をMとします。点M（\(\overrightarrow{m}\)）を通り、辺ABに平行な直線のベクトル方程式を求めましょう。

図がないと理解できないため、位置ベクトルが関わる問題ではまず図を描きましょう。

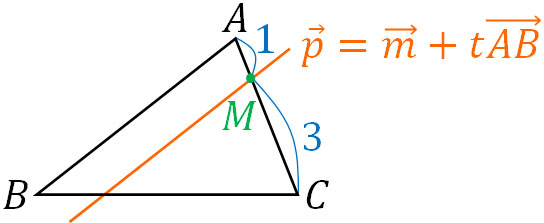
求める直線のベクトル方程式を\(\overrightarrow{p}\)とします。点M（\(\overrightarrow{m}\)）を通り、辺ABに対して平行である必要があるため、位置ベクトルを用いて点P（\(\overrightarrow{p}\)）を表すと以下のようになります。

\(\overrightarrow{p}=\overrightarrow{m}+t\overrightarrow{AB}\)

そこで、位置ベクトルを用いて\(\overrightarrow{m}\)を表しましょう。辺ACを1:3に内分する点がMであるため、以下のように計算できます。

\(\overrightarrow{m}=\displaystyle\frac{3\overrightarrow{a}+\overrightarrow{c}}{1+3}=\displaystyle\frac{3\overrightarrow{a}+\overrightarrow{c}}{4}\)

次に、\(\overrightarrow{p}\)を以下のように計算しましょう。

\(\overrightarrow{p}=\overrightarrow{m}+t\overrightarrow{AB}\)

\(\overrightarrow{p}=\displaystyle\frac{3\overrightarrow{a}+\overrightarrow{c}}{4}+t(\overrightarrow{b}-\overrightarrow{a})\)

\(\overrightarrow{p}=\left(\displaystyle\frac{3}{4}-t\right)\overrightarrow{a}+t\overrightarrow{b}+\displaystyle\frac{1}{4}\overrightarrow{c}\)

こうして、直線の方程式を得ることができました。

2点を通る直線のベクトル方程式

それでは1点ではなく、2点を通る直線を表現するにはどうすればいいのでしょうか。以下のように、点A（\(\overrightarrow{a}\)）と点B（\(\overrightarrow{b}\)）を通る直線を考えてみましょう。

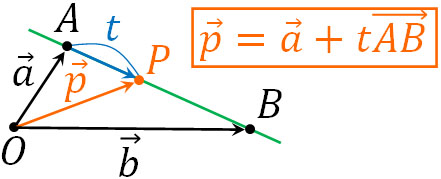
この場合、点Aを通り、辺ABに対して平行な位置ベクトル\(\overrightarrow{p}\)を計算します。そうすると、ベクトル方程式は\(\overrightarrow{p}=\overrightarrow{a}+t\overrightarrow{AB}\)となります。

なお、\(\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}=\overrightarrow{b}-\overrightarrow{a}\)です。そこで、以下のように式を変えましょう。

\(\overrightarrow{p}=\overrightarrow{a}+t\overrightarrow{AB}\)

\(\overrightarrow{p}=\overrightarrow{a}+t(\overrightarrow{b}-\overrightarrow{a})\)

\(\overrightarrow{p}=(1-t)\overrightarrow{a}+t\overrightarrow{b}\)

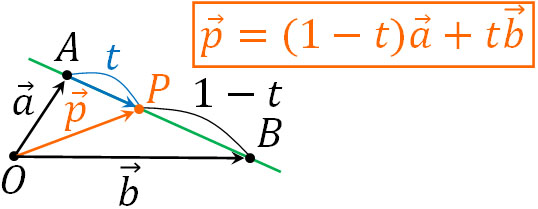
こうして、2点を通る直線のベクトル方程式として\(\overrightarrow{p}=(1-t)\overrightarrow{a}+t\overrightarrow{b}\)を導出できました。それでは、この公式を利用して問題を解きましょう。

2点、A\((1,2)\)とB\((3,5)\)を通る直線の方程式について、媒介変数\(t\)を用いて表しましょう。

位置ベクトルは座標と同じように扱うことができます。そこで、点Pの位置ベクトルを\(\overrightarrow{p}=(x,y)\)として計算しましょう。

\(\overrightarrow{p}=(1-t)\overrightarrow{OA}+t\overrightarrow{OB}\)

\((x,y)=(1-t)(1,2)+t(3,5)\)

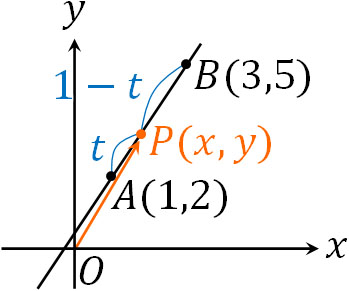
そこで、\(x\)成分と\(y\)成分に分けると以下のようになります。

\(x=2t+1\)
\(y=3t+2\)

こうして、\(\overrightarrow{p}=(2t+1,3t+2)\)とわかりました。参考までに、\(x=2t+1\)と\(y=3t+2\)を用いて\(t\)を消すと\(3x-2y+1=0\)になります。ベクトル方程式は直線を表すため、媒介変数を用いない一次方程式として表すこともできます。

交点の位置ベクトルの計算方法

なお、ベクトルが関わる問題で最も出題される内容の一つが交点の位置ベクトルです。交点を表すとき、\(\overrightarrow{p}=(1-t)\overrightarrow{a}+t\overrightarrow{b}\)を利用するのです。それでは、以下の問題を解いてみましょう。

△OABについて、辺OAを\(1:3\)に内分する点をC、辺OBを\(1:5\)に内分する点をDとします。また、線分ADとBCの交点をP、直線OPと辺ABとの交点をQとします。\(\overrightarrow{OP}\)と\(\overrightarrow{OQ}\)について、\(\overrightarrow{OA}=\overrightarrow{a}\)と\(\overrightarrow{OB}=\overrightarrow{b}\)を用いて表しましょう。

図を描くと以下のようになります。

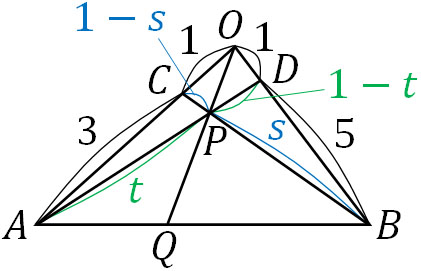
\(\overrightarrow{OP}\)を2つの媒介変数（\(s,t\)）を利用して表します。ベクトル方程式によって直線を表した後、媒介変数を消すことで\(\overrightarrow{OP}\)を得るのです。上図のように媒介変数を利用すると、\(\overrightarrow{OP}\)は以下のようになります。

\(\overrightarrow{OP}=t\overrightarrow{OD}+(1-t)\overrightarrow{OA}\)\(=\displaystyle\frac{1}{6}t\overrightarrow{b}+(1-t)\overrightarrow{a}\)
\(\overrightarrow{OP}=s\overrightarrow{OC}+(1-s)\overrightarrow{OB}\)\(=\displaystyle\frac{1}{4}s\overrightarrow{a}+(1-s)\overrightarrow{b}\)

同じベクトル（\(\overrightarrow{OP}\)）であるため、係数は必ず一致します。つまり、以下の式を作れます。

\(\displaystyle\frac{1}{6}t=1-s\)
\(\displaystyle\frac{1}{4}s=1-t\)

\(\displaystyle\frac{1}{6}t=1-s\)より、\(t=6-6s\)です。そこで、以下のように代入しましょう。

\(\displaystyle\frac{1}{4}s=1-t\)

\(\displaystyle\frac{1}{4}s=1-(6-6s)\)

\(\displaystyle\frac{1}{4}s=-5+6s\)

\(s=-20+24s\)

\(-23s=-20\)

\(s=\displaystyle\frac{20}{23}\)

そこで\(\overrightarrow{OP}=\displaystyle\frac{1}{4}s\overrightarrow{a}+(1-s)\overrightarrow{b}\)に代入すると、\(\overrightarrow{OP}\)\(=\displaystyle\frac{5}{23}\overrightarrow{a}+\displaystyle\frac{3}{23}\overrightarrow{b}\)となります。こうして、\(\overrightarrow{OP}\)を得ることができました。

・\(\overrightarrow{OQ}\)を計算する

考え方は先ほどと同じであり、\(\overrightarrow{OQ}\)を2通りの方法で表しましょう。以下の図を作ります。

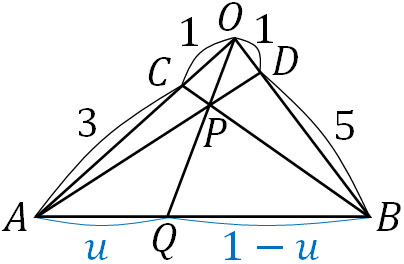
上図のように媒介変数を設定すると、以下のように\(\overrightarrow{OQ}\)を表すことができます。

\(\overrightarrow{OQ}=(1-u)\overrightarrow{a}+u\overrightarrow{b}\)

また\(\overrightarrow{OP}\)を伸ばすと\(\overrightarrow{OQ}\)になるため、\(\overrightarrow{OP}\)\(=k\overrightarrow{OQ}\)と表すことができます。\(\overrightarrow{OP}=\displaystyle\frac{5}{23}\overrightarrow{a}+\displaystyle\frac{3}{23}\overrightarrow{b}\)であるため、以下のようになります。

\(\overrightarrow{OQ}=\displaystyle\frac{5}{23}k\overrightarrow{a}+\displaystyle\frac{3}{23}k\overrightarrow{b}\)

そこで、係数比較をしましょう。

\(1-u=\displaystyle\frac{5}{23}k\)
\(u=\displaystyle\frac{3}{23}k\)

そこで、以下のように計算しましょう。

\(1-u=\displaystyle\frac{5}{23}k\)

\(1-\displaystyle\frac{3}{23}k=\displaystyle\frac{5}{23}k\)

\(1=\displaystyle\frac{8}{23}k\)

\(k=\displaystyle\frac{23}{8}\)

\(k=\displaystyle\frac{23}{8}\)であるため、\(\overrightarrow{OQ}=\displaystyle\frac{5}{23}k\overrightarrow{a}+\displaystyle\frac{3}{23}k\overrightarrow{b}\)に代入すると、\(\overrightarrow{OQ}=\displaystyle\frac{5}{8}\overrightarrow{a}+\displaystyle\frac{3}{8}\overrightarrow{b}\)となります。こうして、\(\overrightarrow{OQ}\)を表すことができました。

定点を通り、特定のベクトルに垂直の直線：法線ベクトル

直角のベクトルを用いてベクトル方程式を表すこともあります。特定の線に対して、垂直な線を法線といいます。法線が大きさと向きをもつ場合、法線ベクトルといいます。

それでは、「定点A（\(\overrightarrow{a}\)）を通り、\(\overrightarrow{0}\)ではないベクトル\(\overrightarrow{n}\)に垂直の直線」をどのように表せばいいでしょうか。特定の点をP（\(\overrightarrow{p}\)）とすると、\(\overrightarrow{AP}\)は点Aから点Pを結ぶベクトルであるため、点Aを通るとわかります。

ただ、点Pの場所によって\(\overrightarrow{AP}\)の向きはさまざまです。そこで、\(\overrightarrow{AP}·\overrightarrow{n}=0\)となる条件を計算しましょう。2つのベクトルが垂直の場合、ベクトルの内積はゼロになります。また\(\overrightarrow{AP}=\overrightarrow{OP}-\overrightarrow{OA}\)\(=\overrightarrow{p}-\overrightarrow{a}\)であるため、以下のように\(\overrightarrow{AP}·\overrightarrow{n}=0\)を変形できます。

\((\overrightarrow{p}-\overrightarrow{a})·\overrightarrow{n}=0\)

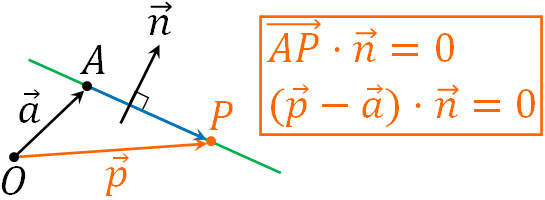
こうして、特定のベクトルに対して垂直な直線となるベクトル方程式の公式を導出できました。それでは、法線ベクトルを利用することで計算問題を解きましょう。以下の問題の答えは何でしょうか。

点A\((1,3)\)を通り、\(-2x+y+3=0\)に平行である直線の方程式\(g\)について、ベクトル方程式を利用して求めましょう。

ベクトル方程式を利用しなくても直線の方程式を得ることはできます。ただ、今回はベクトル方程式を用いて計算します。まず、\(ax+by+c=0\)に対して、\(\overrightarrow{n}=(a,b)\)は直線の法線ベクトルとなります。そのため、\(\overrightarrow{n}=(-2,1)\)は\(-2x+y+3=0\)の法線ベクトルです。

この法則を利用しなくてもいいですが、\(\overrightarrow{n}=(-4,2)\)でも\(\overrightarrow{n}=(-6,3)\)でもいいので、いずれにしても\(-2x+y+3=0\)に対する法線ベクトルを得ましょう。2つの傾きをかけて\(-1\)になる場合、2つの直線は直角に交わります。

それでは、なぜ平行な直線の方程式\(g\)を求めるにも関わらず、法線ベクトルを利用するのでしょうか。\(\overrightarrow{n}\)が直線\(-2x+y+3=0\)に対して垂直なのであれば、直線の方程式\(g\)に対しても垂直になります。つまり、ベクトルの内積がゼロになります。この性質を利用して式を作りましょう。

直線\(g\)上にある任意の点をP\((x,y)\)とします。直線\(g\)は点A\((1,3)\)を通るため、\(\overrightarrow{AP}=\overrightarrow{p}-\overrightarrow{a}\)\(=(x-1,y-3)\)です。また\(\overrightarrow{n}=(-2,1)\)と垂直であるため、以下の式を作りましょう。

\(\overrightarrow{AP}·\overrightarrow{n}=0\)

\(-2×(x-1)+1×(y-3)=0\)

\(-2x+y-1=0\)

こうして、法線ベクトルを利用することによって直線の方程式を得ることができました。