数列の計算ではシグマ記号を利用することがひんぱんにあります。公式を利用して第\(n\)項まで足すのです。
それでは、第\(n\)項ではなく無限大まで足す場合はどのような結果になるのでしょうか。このような数列を無限級数といいます。無限級数が収束または発散するためには条件があるため、これを理解しなければいけません。
また無限等比級数についても、発散と収束の条件を学びましょう。条件を利用することによって和を計算したり、2つの無限等比級数を組み合わせたりできるようになります。
それでは、どのように無限級数の計算をすればいいのでしょうか。収束・発散の条件や無限等比級数の計算方法を解説していきます。
もくじ
シグマ記号の計算の極限が無限級数
数列でシグマ記号を利用して計算するとき、初項から第\(n\)項までを足す計算をします。初項から第\(n\)項までの和を部分和といいます。一方、初項から無限に項を足す場合、無限級数といいます。

そのため無限級数では末項が存在せず、無限に足していくことになります。例えば、以下の無限級数の答えは何でしょうか。
- \(\displaystyle\sum_{k=1}^{∞}{\displaystyle\frac{3n-1}{n^2}}\)
以下のように計算しましょう。
\(\displaystyle\sum_{n=1}^{∞}{\displaystyle\frac{3n-1}{n^2}}\)
\(=\displaystyle \lim_{ n \to \infty } \displaystyle\frac{\displaystyle\frac{3}{2}n(n+1)-n}{\displaystyle\frac{1}{6}n(n+1)(2n+1)}\)
\(=\displaystyle \lim_{ n \to \infty } \displaystyle\frac{9(n+1)-6}{(n+1)(2n+1)}\)
\(=\displaystyle \lim_{ n \to \infty } \displaystyle\frac{9n+3}{2n^2+3n+1}\)
\(=\displaystyle \lim_{ n \to \infty } \displaystyle\frac{\displaystyle\frac{9}{n}+\displaystyle\frac{3}{n^2}}{2+\displaystyle\frac{3}{n}+\displaystyle\frac{1}{n^2}}\)
\(=\displaystyle\frac{0+0}{2+0+0}\)
\(=0\)
このように、シグマ記号の公式と極限の性質を利用することによって計算することができます。
無限級数が収束または発散する条件
それでは、どのようなときに無限級数は収束または発散するのでしょうか。見分け方としては、数列\(\{a_n\}\)が0に収束するかどうかで判断しましょう。\(\displaystyle \lim_{ n \to \infty } a_n≠0\)の場合、無限級数は必ず発散します。
例えば\(\displaystyle \lim_{ n \to \infty } a_n=0.1\)の場合、無限に0.1を足すと答えは\(∞\)になります。これが、\(\displaystyle \lim_{ n \to \infty } a_n≠0\)の場合は無限級数が必ず発散する理由です。
一方、\(\displaystyle \lim_{ n \to \infty } a_n=0\)であっても、無限級数が収束するとは限りません。収束する可能性はあるものの、必ず収束するとは限らないのです。無限級数が収束するかどうかについて、\(\displaystyle \lim_{ n \to \infty } a_n=0\)となるかどうかは目安の一つと考えましょう。
それでは以下の無限級数は収束するでしょうか、それとも発散するでしょうか。
- \(\displaystyle\sum_{n=1}^{∞}{\displaystyle\frac{1}{\sqrt{n+1}+\sqrt{n}}}\)
\(\displaystyle \lim_{ n \to \infty } \displaystyle\frac{1}{\sqrt{n+1}+\sqrt{n}}=0\)であるため、無限級数は収束する可能性があります。そこで、まず部分和を計算しましょう。
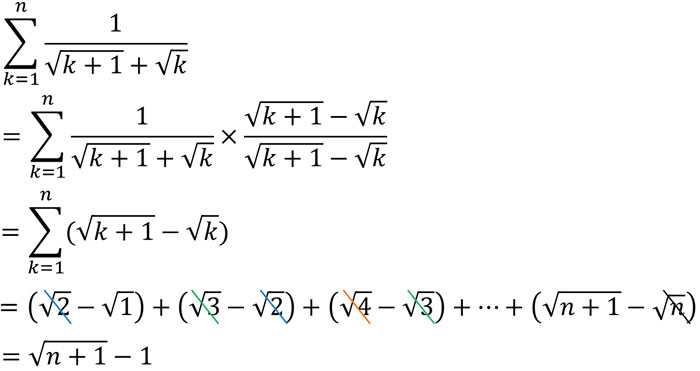
こうして、一般項を得ることができました。なお\(\displaystyle \lim_{ n \to \infty } (\sqrt{n+1}-1)=∞\)であるため、無限級数は発散します。このように、数列の極限が0に収束するとわかっても、無限級数も収束するとは限りません。
無限等比級数の発散と収束:和の公式
次に、等比数列に関する和の極限を計算できるようになりましょう。こうした数列を無限等比級数といいます。等比数列の一般項が\(a_n=ar^{n-1}\)(\(a≠0\))のとき、無限等比級数は以下のようになります。
- \(ar^1+ar^2+ar^3+…\)\(+ar^{n-1}+…\)
このとき無限等比級数が収束するのか、それとも発散するのかは公比\(r\)によって変化します。具体的には、\(|r|<1\)の場合は収束します。\(|r|<1\)の場合、数列の極限は必ず0になり、無限等比級数は特定の値に収束するのです。
なお、等比数列の部分和\(S_n\)は以下の公式によって表されます。
- \(S_n=\displaystyle\frac{a(1-r^n)}{1-r}\)
\(|r|<1\)の場合、\(\displaystyle \lim_{ n \to \infty } r^n=0\)です。そのため、無限等比級数での和は\(\displaystyle\frac{a}{1-r}\)となります。公式を覚えなくても、無限等比級数の意味を知れば公式をそのつど作ることができます。
一方で\(|r|≧1\)の場合、無限等比級数は発散します。数列\(\{a_n\}\)は0に収束しないため、無限等比級数は必ず発散するのです。
- \(|r|<1\)の場合は収束:和は\(\displaystyle\frac{a}{1-r}\)
- \(|r|≧1\)の場合は発散
公比\(r\)の絶対値が1以上か、それとも小さいのかに着目して無限等比級数の計算をしましょう。それでは、以下の無限等比級数の和はいくらでしょうか。
- \(\displaystyle\sum_{n=1}^{∞}{\left(\displaystyle\frac{1}{2}\right)^ncos\ nπ}\)
この式では理解しにくいため、実際に\(n=1,2,3…\)と代入しましょう。
- \(-\displaystyle\frac{1}{2}+\left(\displaystyle\frac{1}{2}\right)^2-\left(\displaystyle\frac{1}{2}\right)^3\)\(+\left(\displaystyle\frac{1}{2}\right)^4-…\)
このように初項\(-\displaystyle\frac{1}{2}\)、公比\(-\displaystyle\frac{1}{2}\)の無限等比級数とわかります。\(|r|<1\)であるため、和を計算できます。
\(\displaystyle\frac{-\displaystyle\frac{1}{2}}{1-\left(-\displaystyle\frac{1}{2}\right)}\)
\(=-\displaystyle\frac{1}{3}\)
こうして、答えを得ることができました。
循環小数を分数へ直す無限等比級数の利用
無限等比級数を利用すれば、循環小数を分数へ変換することも可能です。循環小数は無限等比級数でもあるからです。それでは、\(0.353535…\)を分数で表すとどのようになるでしょうか。以下のように計算しましょう。
\(0.353535…\)
\(=0.35+0.0035\)\(+0.000035+…\)
\(=0.35+0.35×\displaystyle\frac{1}{100}\)\(+0.35×\left(\displaystyle\frac{1}{100}\right)^2+…\)
このように初項0.35、公比\(\displaystyle\frac{1}{100}\)の無限等比級数です。そこで、以下のように計算しましょう。
\(\displaystyle\frac{0.35}{1-\displaystyle\frac{1}{100}}\)
\(=\displaystyle\frac{35}{99}\)
こうして、循環小数を分数へ変換することができました。
2つの無限等比級数の和
それでは、2つの無限等比級数を足すときはどのように計算すればいいのでしょうか。無限等比級数が発散する場合、当然ながら答えは\(∞\)または\(-∞\)です。そこで、特定の値に収束する無限等比級数を考えましょう。
例えば\(\displaystyle\sum_{n=1}^{∞}{a_n}=A\)、\(\displaystyle\sum_{n=1}^{∞}{b_n}=B\)となる場合、以下の計算になります。
- \(\displaystyle\sum_{n=1}^{∞}{(a_n+b_n)}\)\(=A+B\)
この結果は容易に理解できると思います。またそれぞれの無限等比級数を\(k\)倍、\(l\)倍する場合、以下の計算になります。
- \(\displaystyle\sum_{n=1}^{∞}{(ka_n+lb_n)}\)\(=kA+lB\)
無限等比級数が複数存在する場合であっても、計算方法は変わりません。それぞれの数列について極限を計算した後、かけ算と足し算をしましょう。
収束や発散に着目して無限級数の計算を行う
無限級数の計算では、収束または発散することになります。無限級数を計算するとき、部分和を求めましょう。公式を利用することにより、部分和を得た後に数列の極限を利用するのです。これにより、無限級数の計算が可能になります。
なお、数列の極限が0以外の場合、無限級数は必ず発散します。一方で数列の極限が0になる場合、無限級数は収束する可能性があります。実際に収束するかどうかは計算しなければわかりません。
また無限等比数列の計算も行えるようになりましょう。公比\(r\)に着目することで収束するのか、それとも発散するのか判断するのです。なお無限級数が収束する場合、和の公式を利用することで答えを得ることができます。
シグマ記号を用いる計算を発展させた数列が無限級数です。シグマ記号を用いて計算した後、数列の極限を利用することで答えを得ましょう。