平面ベクトル：足し算・引き算や平行条件、距離の計算

大きさに加えて、特定の向きをもつ概念にベクトルがあります。日常生活でベクトルが利用されているケースは多く、力やスピードなどは向きをもっています。

そこで大きさと向きをもつケースでの計算方法を学びましょう。向きがある場合、\(3+4=7\)になるとは限りません。ベクトルの大きさを計算すると、\(3+4=5\)になることもあります。

なお座標を利用することにより、ベクトルが何を意味しているのか理解できるようになります。特に物理では、ベクトルがひんぱんに利用されます。ベクトルを学んでいないと、力学の計算はできません。そのため、数学以外の分野でもベクトルは重要です。

それでは、どのようにベクトルを用いて計算すればいいのでしょうか。ベクトルの概念や計算方法、座標の利用法について解説していきます。

1 ベクトルの向きと概要
- 1.1 ベクトルの足し算、引き算：実数倍と単位ベクトル
2 ベクトルの成分と大きさ（長さ）
3 座標とベクトルの大きさの関係
- 3.1 ベクトルの大きさの最小値
4 大きさと向きをもつ要素を計算する

ベクトルの向きと概要

大きさ（数字）だけでなく、向きも重要であることは多いです。例えば温度や重さには向きがありません。プラスとマイナスはあるものの、特定の向きに温度が移動することはないのです。

一方で力や速さには向きがあります。例えば、北向き3m/sで進んでいるボールに対して、右向き（東向き）に4m/sの力を一瞬加える場合、ボールの速さはいくらになるでしょうか。

ベクトルでは、方向の異なる2つの力を足すことができます。そこで以下のように図を作り、三平方の定理を利用すると、ボールの速さは5m/sになることがわかります。

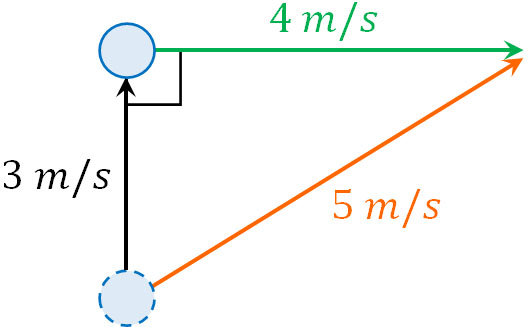
ベクトルを学ぶ前では、速さの計算では同じ向き、または反対向きのみです。同じ向きの場合は足せばいいし、反対向きなら引けばいいです。なお、反対向きのベクトルを逆ベクトルといいます。

ただ向きが同じであったり、逆ベクトルではなかったりするケースは多いです。力や速さには、さまざまな向きがあります。そこで、向きを考慮して計算しなければいけません。

ベクトルの足し算、引き算：実数倍と単位ベクトル

なおベクトルの足し算は複雑ではありません。例えば\(\overrightarrow{OA}\)と\(\overrightarrow{OB}\)がある場合、以下のように足しましょう。

\(\overrightarrow{OA}+\overrightarrow{OB}\)

\(\overrightarrow{OA}\)の先に\(\overrightarrow{OB}\)を加え、三角形を作ることで、新たなベクトル（\(\overrightarrow{c}\)）を得ることができます。または、上図のように平行四辺形を作り、対角線を引くことで新たなベクトル（\(\overrightarrow{c}\)）を得ることもできます。どちらの方法を利用しても問題ありません。

一方で引き算をするとき、逆ベクトルを用いましょう。例えば\(\overrightarrow{OA}\)から\(\overrightarrow{OB}\)を引く場合、\(\overrightarrow{OB}\)の逆ベクトルを利用します。以下のようになります。

\(\overrightarrow{OA}-\overrightarrow{OB}\)

ベクトルの足し算や引き算では、ベクトルの大きさが変化するだけでなく、ベクトルの向きも変わります。

なお、ベクトルを実数倍することもあります。計算方法は簡単であり、実数倍の分だけベクトルの大きさを増やしましょう。例えば2倍する場合、ベクトルの大きさは2倍になります。また\(\displaystyle\frac{1}{2}\)倍する場合、ベクトルの大きさは半分になります。

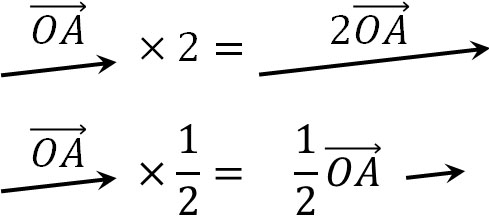
ベクトルを実数倍する場合、ベクトルの向きに変化はありません。ただ負の実数をかける場合、当然ながらベクトルの向きは逆になります。

なお大きさ（長さ）が1のベクトルを単位ベクトルといいます。このときベクトルの大きさ（長さ）は\(|\overrightarrow{AB}|\)や\(|\overrightarrow{a}|\)と表します。例えば\(|\overrightarrow{a}|=3\)の場合、長さは3であり、\(\overrightarrow{a}\)に平行な単位ベクトルは\(\displaystyle\frac{\overrightarrow{a}}{3}\)と\(-\displaystyle\frac{\overrightarrow{a}}{3}\)です。

ベクトルの成分と大きさ（長さ）

それでは、ベクトルの大きさを計算できるようになりましょう。ベクトルの演算方法は以下になります。

交換法則：\(\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{b}+\overrightarrow{a}\)
結合法則：\((\overrightarrow{a}+\overrightarrow{b})+\overrightarrow{c}\)\(=\overrightarrow{a}+(\overrightarrow{b}+\overrightarrow{c})\)
ゼロベクトル：\(\overrightarrow{AA}=\overrightarrow{0}=|\overrightarrow{0}|\)
逆ベクトル：\(\overrightarrow{a}-\overrightarrow{a}=\overrightarrow{0}\)
0の性質：\(\overrightarrow{a}-\overrightarrow{0}=\overrightarrow{a}\)
実数倍：\(k(\overrightarrow{a}+\overrightarrow{b})=k\overrightarrow{b}+k\overrightarrow{a}\)
実数倍：\((k+l)\overrightarrow{a}=k\overrightarrow{a}+l\overrightarrow{a}\)
実数倍：\(k(l\overrightarrow{a})=kl\overrightarrow{a}\)

これらの内容は難しくなく、ベクトルの計算で利用できるようになりましょう。

なおベクトルの計算では、座標と同じ方法を利用して成分を記します。例えば\(\overrightarrow{a}=(4,3)\)の場合、\(xy\)平面では\(x\)軸方向に4、\(y\)軸方向に3のベクトルを意味します。また三平方の定理を利用すると、大きさ（ベクトルの長さ）は5になるので\(|\overrightarrow{a}|=5\)です。

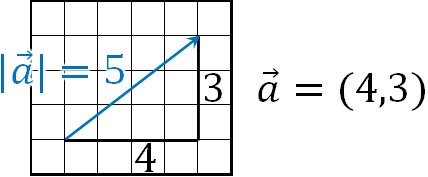
数学で座標の計算をするとき、\(x\)軸と\(y\)軸を分けて計算する必要があります。そのためベクトルについても、2つの成分（\(x\)成分と\(y\)成分）を分けて考えましょう。

なお\(x\)成分と\(y\)成分を利用してベクトルの成分を表すため、必ず直角三角形を作れます。そのため\(\overrightarrow{a}=(a_1,a_2)\)の場合、以下のようにベクトルの大きさ（長さ：\(|\overrightarrow{a}|\)）を計算できます。

\(|\overrightarrow{a}|=\sqrt{a_1^2+a_2^2}\)

\(\overrightarrow{a}\)というのは、\(\overrightarrow{a}=(4,3)\)のようにベクトル成分で表すことができます。一方で\(|\overrightarrow{a}|\)は\(\overrightarrow{a}\)の長さを表します。ベクトルの計算をするとき、記号の意味を学びましょう。

成分を用いてベクトルの足し算、引き算、実数倍を行う

\(x\)成分と\(y\)成分に分ければ足し算、引き算、実数倍をするのも容易です。ベクトルの計算というのは、座標を利用する計算と似ています。例えば\(\overrightarrow{a}=(4,3)\)、\(\overrightarrow{b}=(2,5)\)の場合、以下のように計算しましょう。

\(\overrightarrow{a}+\overrightarrow{b}=(4,3)+(2,5)\)\(=(6,8)\)

\(\overrightarrow{a}-\overrightarrow{b}=(4,3)-(2,5)\)\(=(2,-2)\)

\(\overrightarrow{a}+2\overrightarrow{b}=(4,3)+(4,10)\)\(=(8,13)\)

それぞれの成分に分けて計算すればいいため、特に難しくないと思います。

ベクトル成分の分解と計算

なお、一つのベクトルを2つのベクトルで表すことが可能です。それでは以下のようにベクトルがあるとき、\(\overrightarrow{b}\)と\(\overrightarrow{c}\)を用いて\(\overrightarrow{a}\)を表すにはどうすればいいでしょうか。

前述の通り、ベクトルを実数倍することができます。そこで\(\overrightarrow{b}\)と\(\overrightarrow{c}\)の長さをそれぞれ\(k\)倍、\(l\)倍して変えれば、以下のように\(\overrightarrow{a}\)を作れます。

\(\overrightarrow{a}=k\overrightarrow{b}+l\overrightarrow{c}\)

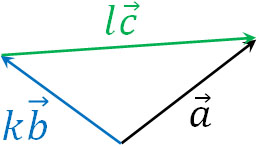
このように\(\overrightarrow{b}\)と\(\overrightarrow{c}\)について特定の値で実数倍したあと、2つのベクトルを組み合わせることによって\(\overrightarrow{a}\)を作ることができました。このように、ベクトルの分解が可能です。

それでは、以下の問題の答えは何でしょうか。

\(\overrightarrow{a}=(1,1)\)、\(\overrightarrow{b}=(2,-1)\)、\(\overrightarrow{c}=(5,2)\)のとき、\(\overrightarrow{c}=s\overrightarrow{a}+t\overrightarrow{c}\)を満たす\(s\)と\(t\)を求めましょう。

\(x\)成分と\(y\)成分に分けて以下の式を作りましょう。

\(x\)成分：\(s+2t=5\) – ①
\(y\)成分：\(s-t=2\) – ②

\(①-②\)より、\(t=1\)です。そのため、\(s=3\)です。つまり、\(\overrightarrow{c}=3\overrightarrow{a}+\overrightarrow{c}\)です。こうして、ベクトルを分解することができました。参考までに、\(\overrightarrow{a}=(1,1)\)であるため、\(\overrightarrow{a}\)は単位ベクトルです。

平行条件とベクトルの利用

ベクトルでは平行条件を利用して計算することもあります。2つのベクトルが平行な場合、実数倍になります。例えば\(\overrightarrow{a}\)と\(\overrightarrow{b}\)が平行な場合、以下の関係が成り立ちます（\(k\)は実数）。

\(\overrightarrow{a}=k\overrightarrow{b}\)

この関係は問題なく理解できると思います。ベクトルには向きがあるため、特定の値で実数倍することで同じになる場合、2つのベクトルは平行です。

なお2つのベクトルが平行な場合、それぞれのベクトルについて、\(x\)成分と\(y\)成分の比は等しくなります。そのため\(\overrightarrow{a}=(a_1,a_2)\)と\(\overrightarrow{b}=(b_1,b_2)\)が平行の場合、以下のようになります。

\(a_1:a_2=b_1:b_2\)

\(a_1b_2=a_2b_1\)

そのため、以下の関係が成り立ちます。

\(a_1b_2-a_2b_1=0\)

これがベクトルの平行条件です。それでは、以下の問題の答えは何でしょうか。

\(\overrightarrow{a}=(14,-2)\)、\(\overrightarrow{b}=(3t+1,-4t+7)\)が平行になるとき、\(t\)の値を計算しましょう。

2つのベクトルは平行であるため、\(k\overrightarrow{a}=\overrightarrow{b}\)となります。\(\overrightarrow{a}=k\overrightarrow{b}\)と考えてもいいですが、計算が複雑になるため、\(k\overrightarrow{a}=\overrightarrow{b}\)と考えます。そこで、以下の式を作りましょう。

\(x\)成分：\(14k=3t+1\) – ①
\(y\)成分：\(-2k=-4t+7\) – ②

\(①+②×7\)より、以下のように計算しましょう。

\(-25t+50=0\)

\(t=2\)

こうして、\(t=2\)のときに\(\overrightarrow{a}\)と\(\overrightarrow{b}\)が平行になるとわかります。

座標とベクトルの大きさの関係

座標と同様にベクトルを成分で表せることを学べば、2つの点を結ぶベクトルの成分と大きさ（ベクトルの長さ）を計算できます。

例えば、点A\((a_1,a_2)\)と点B\((b_1,b_2)\)があるとします。このとき、点Aと点Bについて\(x\)成分と\(y\)成分はそれぞれ以下のようになります。

\(x\)成分：\(b_1-a_1\)
\(y\)成分：\(b_2-a_2\)

なお、上図は\(\overrightarrow{AB}\)を表します。つまり、点Aから点Bにベクトルを作る場合、ベクトルの成分は以下のようになります。

\(\overrightarrow{AB}=(b_1-a_1,b_2-a_2)\)

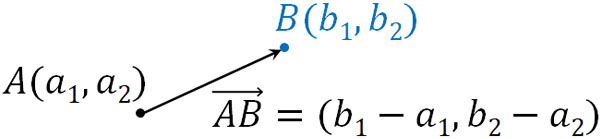
なお\(x\)成分と\(y\)成分を利用して距離を計算することができます。\(\overrightarrow{AB}=(b_1-a_1,b_2-a_2)\)であるため、三平方の定理を利用すると以下の計算式になります。

\(|\overrightarrow{AB}|\)\(=\sqrt{(b_1-a_1)^2+(b_2-a_2)^2}\)

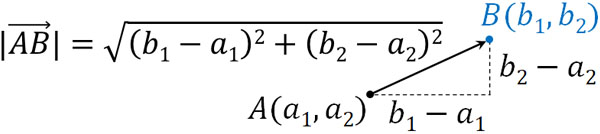
それでは、以下の問題の答えは何でしょうか。

点A\((2,5)\)と点B\((6,-1)\)について、\(\overrightarrow{AB}\)の成分とベクトルの長さを計算しましょう。

\(\overrightarrow{AB}\)の成分は以下のように計算できます。

\(\overrightarrow{AB}=(6-2,-1-5)\)

\(\overrightarrow{AB}=(4,-6)\)

また、\(\overrightarrow{AB}\)の大きさ（長さ）を以下のように計算しましょう。

\(|\overrightarrow{AB}|=\sqrt{4^2+(-6)^2}\)

\(|\overrightarrow{AB}|=\sqrt{16+36}\)

\(|\overrightarrow{AB}|=\sqrt{52}\)

\(|\overrightarrow{AB}|=2\sqrt{13}\)

こうして、\(|\overrightarrow{AB}|=2\sqrt{13}\)とわかりました。

ベクトルの大きさの最小値

それでは、ベクトルの大きさが最小となる値を計算できるようになりましょう。ここまで解説した内容を理解すれば、ベクトルの大きさの最小値を得ることができます。以下の問題の答えは何でしょうか。

\(\overrightarrow{a}=(3,1)\)、\(\overrightarrow{b}=(2,-1)\)のとき、\(|\overrightarrow{a}+t\overrightarrow{b}|\)の最小値を計算しましょう。

\(|\overrightarrow{a}+t\overrightarrow{b}|\)というのは、\(\overrightarrow{a}+t\overrightarrow{b}\)の大きさ（ベクトルの距離）を指します。そこで、\(\overrightarrow{a}+t\overrightarrow{b}\)の成分を計算しましょう。それぞれ以下のようになります。