二項定理：パスカルの三角形と多項定理の計算・公式

数学で学ぶ内容に二項定理があります。\((a+b)^n\)を展開するとき、係数を調べたいときに役に立つのが二項定理です。

二項定理では、組み合わせ（\(_nC_r\)）を利用します。そこで二項定理の考え方を学び、なぜ二項定理の公式で組み合わせを使うのか理解しましょう。それに加えて、二項定理の証明をすれば、二項定理の計算方法をより深く理解できるようになります。

また二項定理と関係ある計算にパスカルの三角形があります。パスカルの三角形を利用して、二項定理の計算をしても問題ありません。また二項定理の発展問題に多項定理の計算があります。多項定理についても、公式を利用して計算できるようになりましょう。

それでは、二項定理ではどのような公式を利用して計算問題を解けばいいのでしょうか。二項定理だけでなく、パスカルの三角形や多項定理を含めて解説していきます。

1 二項定理の公式と計算方法
- 1.1 二項定理の証明と考え方
- 1.2 パスカルの三角形と二項定理の関係
2 多項定理の展開式の考え方
- 2.1 分数を含む場合の多項展開式の計算：定数項を求める
- 2.2 nケタの数を得る二項定理の利用
3 二項定理と多項定理の公式がもつ意味を学ぶ

二項定理の公式と計算方法

文章を読むことで二項定理を理解するのは難しいです。そこで、具体例を用いて二項定理を学びましょう。まず、例として\((a+b)^2=(a+b)(a+b)\)を計算します。

多項式を展開するとき、以下のように分配法則を利用して計算することになります。

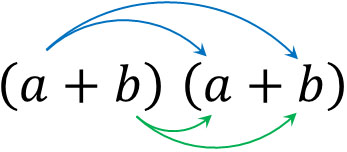
こうして、以下のように計算します。

\((a+b)^2=a^2+2ab+b^2\)

それでは、計算過程をより詳細に確認しましょう。\((a+b)(a+b)\)の計算をするとき、「異なる2つのかっこ（）の中から、\(b\)を何回選ぶのか」によって、項の係数が決まります。

例えば\((a+b)(a+b)\)について、2つのかっこ（）から\(b\)を0回選ぶ場合、\(_2C_0\)となり、項の係数は1です。また2つのかっこ（）から\(b\)を1回選ぶ場合、\(_2C_1\)となり、項の係数は2です。2つのかっこ（）から\(b\)を2回選ぶ場合、\(_2C_2\)となり、項の係数は1です。

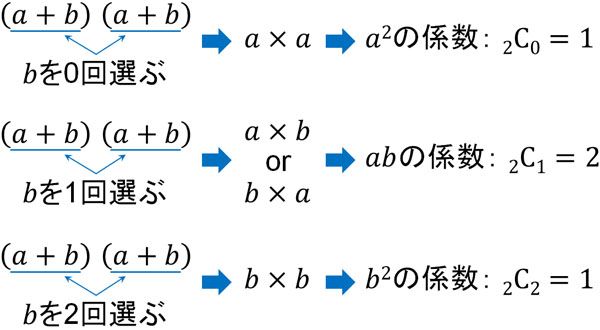
そのため、展開するときの係数は組み合わせを利用することによって計算できます。

\((a+b)^2\)

\(=_2C_0a^2+_2C_1ab+_2C_2b^2\)

\(=a^2+2ab+b^2\)

それでは\((a+b)^3\)を計算するとき、例えば\(ab^2\)の係数は何でしょうか。かっこ（）は合計で3つあり、その中から\(b\)を2つ選ぶと\(ab^2\)を得られます。そのため、\(ab^2\)の係数は\(_3C_2=3\)です。

・二項定理の公式

なお、二項定理の公式は以下になります。

\((a+b)^n\)

\(=_nC_0a^n+_nC_1a^{n-1}b+_nC_2a^{n-2}b^2…\)\(+_nC_ra^{n-r}b^r+…\)\(+_nC_nb^n\)

ただ、この公式を見ても意味を理解できません。そのため公式を覚えるのではなく、二項定理の公式が何を意味しているのか学びましょう。そうすれば、公式を覚えなくても二項定理を利用して計算できます。

二項定理の証明と考え方

先ほどの考え方を利用すれば、二項定理の証明は難しくありません。\((a+b)^n\)では、かっこの数が\(n\)個です。

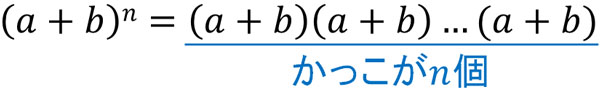
そのため\(a^{n-r}b^r\)の係数を計算するためには、かっこの中から\(b\)を\(r\)回、選べばいいです。つまり、\(_nC_r\)（または\(_nC_{n-r}\)）を計算すれば項の係数を計算できます。

また、それぞれの項と係数をかけた後、すべて足すと展開式になります。こうして、先ほどの公式を導出できます。証明の方法はいくつか存在するものの、二項定理の考え方を利用すれば、なぜ先ほどの公式が成り立つのかわかります。

・二項定理の練習問題

それでは、二項定理の公式を利用して計算しましょう。以下の問題の答えは何でしょうか。

\((x-2)^5\)を展開するとき、\(x^3\)の係数を求めましょう。

\((x-2)^5\)を展開するとき、かっこの数は5個です。また\(x\)を3回（または-2を2回）選ぶことにより、\(x^3\)を含む項になります。そこで、以下のように計算しましょう。

\(_5C_2x^3(-2)^2=40x^3\)

こうして、\(x^3\)の係数は40になるとわかりました。

パスカルの三角形と二項定理の関係

なお、二項定理と関係の深い概念にパスカルの三角形があります。パスカルの三角形では、頂点を1に設定します。その後、三角形を作るように左右の数を足します。そうすると、以下の三角形を作ることができます。

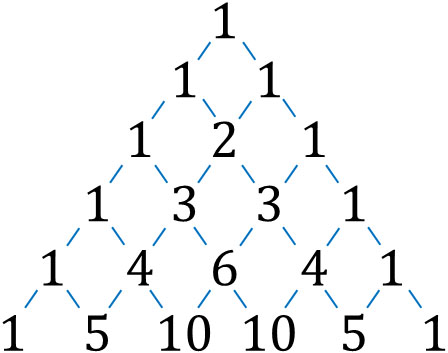
これがパスカルの三角形です。パスカルの三角形を確認すると、数字は二項定理の係数に相当しているとわかります。

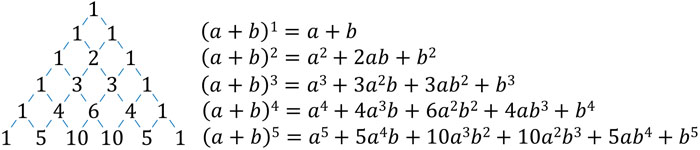
そのため二項定理の計算をするとき、パスカルの三角形を利用して答えを得ることもできます。どちらの方法であっても正解を得ることが可能なのです。

ただ累乗の数が大きい場合、パスカルの三角形を利用して答えを得るのは現実的ではありません。その場合、二項定理の公式を利用することで計算しましょう。

多項定理の展開式の考え方

二項定理の発展問題として多項定理があります。例として、三項の式を展開する場合の係数を計算できるようになりましょう。以下の式を展開するのです。

\((a+b+c)^n\)

それでは、この場合の係数を計算するためにはどのように考えればいいのでしょうか。考え方は先ほどと同じであり、かっこの数に着目しましょう。\((a+b+c)^n\)には、かっこが\(n\)個含まれています。

このとき「\(a^pb^qc^r\)を含む項というのは、\(n\)個存在するかっこの中から\(a\)を\(p\)回、\(b\)を\(q\)回、\(c\)を\(r\)回選ぶ順列である」と考えることができます。そのため、以下が\(a^pb^qc^r\)の係数を得る公式です。

\(\displaystyle\frac{n!}{p!q!r!}\)

そのため\((a+b+c)^n\)を展開するとき、以下のように一般項を表すことができます。

\(\displaystyle\frac{n!}{p!q!r!}a^pb^qc^r\)

この公式を暗記しても意味がなく、なぜこの公式によって計算できるのか学びましょう。そうすれば、公式を覚えなくても公式の導出が可能です。

なお当然ながら、かっこの数は\(n\)個であるため、\(p+q+r=n\)を満たします。また\(p≧0\)、\(q≧0\)、\(r≧0\)です。

※\(0!=1\)と定めます。

分数を含む場合の多項展開式の計算：定数項を求める

それでは、多項定理の計算問題を解いてみましょう。以下の問題の答えは何でしょうか。

\(\left(x+\displaystyle\frac{1}{x}-1\right)^8\)の展開式について、定数項（次数が0になる項）を求めましょう。

まず、\(\left(x+\displaystyle\frac{1}{x}-1\right)^8\)を展開するときの一般項を求めましょう。以下のようになります。

\(\displaystyle\frac{8!}{p!q!r!}x^p\left(\displaystyle\frac{1}{x}\right)^q(-1)^r\)\(=\displaystyle\frac{8!}{p!q!r!}x^{p-q}(-1)^r\)

なお、\(p,q,r\)は\(p+q+r=8\)を満たす正の整数です。

先ほどの式を確認してわかる通り、項の次数がゼロになるためには、\(p-q=0\)になる必要があります。つまり、\(p=q\)です。\(p=q\)と\(p+q+r=8\)を満たす正の整数\(p,q,r\)は以下になります。

\(0,0,8\)
\(1,1,6\)
\(2,2,4\)
\(3,3,2\)
\(4,4,0\)

この4つのケースでは、次数が0になります。そこで多項定理の展開式を利用し、以下のように計算して定数項を求めましょう。

\(\displaystyle\frac{8!}{8!}(-1)^8+\displaystyle\frac{8!}{6!}(-1)^6+\displaystyle\frac{8!}{2!2!4!}(-1)^4\)\(+\displaystyle\frac{8!}{3!3!2!}(-1)^2\)\(+\displaystyle\frac{8!}{4!4!}(-1)^0\)

\(=1+56+420+560+70\)

\(=1107\)

こうして、定数項は1107と計算できました。