確率の計算と性質：加法定理や和事象、余事象の利用

順列と組み合わせを理解することにより、何通りの方法があるのか計算できる場合、確率の計算ができるようになります。全事象に対して、特定の事象が起こるパターンを計算することによって確率を求めることができるのです。

なお確率の計算をするとき、確率にはいくつか性質があります。確率の性質を利用することによって、足し算によって答えを出すことができたり、重複を除くことによって確率の計算ができたりします。

また起こらない確率を計算したい場合、起こる確率を利用することによって計算できます。起こらない事象を余事象と呼び、確率の性質を利用することによって計算できるのです。

確率の計算をするとき、事前に性質を学びましょう。そこで、確率の計算方法や性質を解説していきます。

確率の計算方法：全体と事象を計算する

順列と組み合わせを利用し、何通りの方法があるのか計算できるようになったら、次に確率の計算をしましょう。確率の計算では、まず全体の事象が何通りあるのか数えます。また、特定の事象Aが起こる回数を数えます。その後、事象Aに対して全体の事象で割ります。

例えば、サイコロを2つ投げて出る目の和が3になる確率はいくらでしょうか。サイコロを2つ投げるとき、全体の事象は\(6×6=36\)通りの方法があります。一方、目の和が3になるのは2通りあります。

• (1, 2) (2, 1)

そのため、事象の場合の数は2です。そこで、以下のように分子を2、分母を36にします。

• \(\displaystyle\frac{2}{36}=\displaystyle\frac{1}{18}\)

こうして、確率を計算することができます。

個数に着目し、確率の計算を行う

なお確率の計算をするとき、個数に着目するようにしましょう。要素が何個あるのか数えるのです。例えば、以下の問題の答えは何でしょうか。

• 白玉が3つ、赤玉が2つあります。無造作に同時に2つ取り出すとき、白玉1つ、赤玉1つの確率はいくらですか？

色だけに着目する場合、（白、白）（白、赤）（赤、赤）となります。そのため人によっては、\(\displaystyle\frac{1}{3}\)が答えであると考えます。ただ、これは間違いです。そこで白や赤などの色だけでなく、個数も着目して確率を計算しましょう。

まず、全体の場合の数は₅C₂です。また、白玉1つと赤玉1つを取り出す場合の数は₃C₁と₂C₁です。そのため、以下の式になります。

\(\displaystyle\frac{_3C_1×_2C_1}{_5C_2}=\displaystyle\frac{3}{5}\)

このように玉の個数を考慮することによって、確率の計算を行えるようになります。

確率から含まれる要素の数を計算する

なお確率の問題では、すでにわかっている確率から、いくつの要素が含まれているのか計算することもあります。この場合、確率を利用することによって答えを出しましょう。例えば、以下の問題の答えは何でしょうか。

• 16本のクジがあり、この中から同時に2本を引くと、1本が当たりで1本がはずれになる確率が\(\displaystyle\frac{7}{30}\)です。当たりのクジは何本入っていますか？

この問題の答えを出すためには、当たりのクジがn本入っていると考えて、式を作らなければいけません。

全事象の数は₁₆C₂です。またn本の当たりクジがあるため、一本が当たりを引くケースは_nC₁です。またはずれの数は(16-n）本であり、この中から一本を選ぶケースは_(n-1)C₁です。そのため、以下の式を作ることができます。

• \(\displaystyle\frac{_nC_1×_{(16-n)}C_1}{_{16}C_2}=\displaystyle\frac{7}{30}\)

\(_nC_1=n\)であり、\(_{(16-n)}C_1=16-n\)です。そのため、以下のように計算できます。

\(\displaystyle\frac{_nC_1×_{(16-n)}C_1}{_{16}C_2}=\displaystyle\frac{7}{30}\)

\(\displaystyle\frac{n(16-n)}{120}=\displaystyle\frac{7}{30}\)

\(\displaystyle\frac{16n-n^2}{4}=7\)

\(16n-n^2=28\)

\(n^2-16n+28=0\)

\((n-2)(n-14)=0\)

\(1≦n≦15\)であるため、\(n=2\)または\(n=14\)が答えです。つまり、当たりのクジの数は2本または14本です。こうして、結果を利用して未知数を計算することができます。

確率では全事象が必ず1になる

なお確率では、全事象を1とします。そのため確率で答えがマイナスになることはないですし、1を超えることもないです。すべての事象を足して答えが1を超える場合、計算方法を間違えています。

Aが起こる確率\(P(A)\)は必ず\(0≦P(A)≦1\)になります。またAに何も含まれていない場合、空事象Φが起こる確率は\(P(Φ)=0\)です。また全事象Uが起こる確率は\(P(U)=1\)です。

確率の性質を理解するとき、最初に覚えなければいけない性質が「全事象が起こる確率は必ず1になる」ことです。

排反事象の場合、加法定理によって足し算をする

次に加法定理を理解しましょう。二つの事象について、同時に起こることがない場合、AとBは互いに排反事象といえます。また排反事象の場合、独立している事象であるため、AまたはBが起こる確率を足すことができます。

つまり、AまたはBが起こる確率\(P(A∪B)\)は以下のように足し算によって計算できます。

• \(P(A∪B)=P(A)+P(B)\)

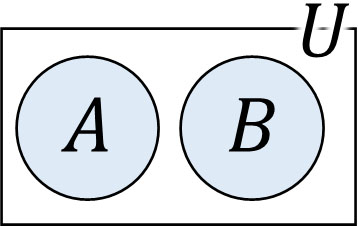
これを加法定理といいます。それでは、加法定理を利用して確率を計算してみましょう。以下の問題の答えは何でしょうか。

• 2つのサイコロを振り、目の和が4の倍数になる確率はいくらでしょうか？

目の和が4の倍数になるためには、足して4または8または12になればいいです。以下のケースで4の倍数になります。

• 足して4：(1,3) (2, 2) (3, 1)
• 足して8：(2, 6) (3, 5) (4, 4) (5, 4) (6, 2)
• 足して12：(6, 6)

目の和が4になり、同時に目の和が8になることはありません。そのためそれぞれの事象は同時に起こることがなく、独立しています。また、目の和が4の倍数になるすべての事象を数えると、上記のように合計は9です。2つのサイコロを投げるとき、全部で36通りの方法があるため、4の倍数になる確率は以下になります。

• \(\displaystyle\frac{9}{36}=\displaystyle\frac{1}{4}\)

2つの事象が互いに排他事象の場合、加法定理によって足し算をしましょう。

和事象の確率では、足し算の後に重複部分を引く

一方で排他事象ではない場合、どのように計算すればいいのでしょうか。この場合、和事象の確率を計算しましょう。以下のように事象Aと事象Bで重なっている部分がある場合、事象Aの確率\(P(A)\)と事象Bの確率\(P(B)\)を足した後、AとBが重なっている部分\(P(A∩B)\)を引くのです。

和事象の確率では、足した後に重なっている部分を引けばいいため、考え方は難しくありません。

ちなみにAとBの2つの事象について、AとBが同時に起こる確率を積事象といいます。和事象の確率を出すためには、Aの確率とBの確率を足した後、AとBの積事象\(P(A∩B)\)を引きましょう。

なぜ積事象なのかというと、2つの事象が同時に起こる場合、かけ算をすることによって答えを出すからです。例えば2つのサイコロを振り、1の目と2の目が出る確率はいくらでしょうか。1の目が出る確率は\(\displaystyle\frac{1}{6}\)です。また2の目が出る確率は\(\displaystyle\frac{1}{6}\)です。そのため、以下のように積事象を計算できます。

• \(\displaystyle\frac{1}{6}×\displaystyle\frac{1}{6}=\displaystyle\frac{1}{36}\)

同時に起こる確率\(P(A∩B)\)を計算したいとき、かけ算を利用します。それでは、実際に和事象の確率を計算してみましょう。以下の問題の答えは何でしょうか。

• 1から100までの番号が書かれたカードが100枚あります。この中から無造作に1枚のカードを選ぶとき、カードの番号が4または5の倍数になる確率はいくらでしょうか？

全事象は100です。このうち、4の倍数になるケースは25通りです。また5の倍数になるケースは20通りです。

• 4の倍数：4×1, 4×2, 4×3, …, 4×25
• 5の倍数：5×1, 5×2, 5×3, …, 5×20

ただ4の倍数であり、5の倍数でもあるケースがあります。20の倍数では、両方の条件を満たしてしまいます。そこで積事象（20の倍数）を考慮しましょう。20の倍数になるケースは5通りです。

• 20の倍数：20×1, 20×2, 20×3, 20×4, 5×20

また前述の通り、全事象は100なので以下の計算によって確率を求めることができます。

\(\displaystyle\frac{25}{100}+\displaystyle\frac{20}{100}-\displaystyle\frac{5}{100}=\displaystyle\frac{40}{100}=\displaystyle\frac{2}{5}\)

和事象の確率を計算するとき、それぞれの確率に加えた後、積事象を引きましょう。

起こる確率を計算し、余事象の確率を出す

なお事象Aに対して、事象Aが起こらないケースを余事象といいます。事象Aが起こる確率を\(P(A)\)とすると、余事象が起こる確率\(P(\overline{A})\)は以下の計算によって求めることができます。

• \(P(\overline{A})=1-P(A)\)

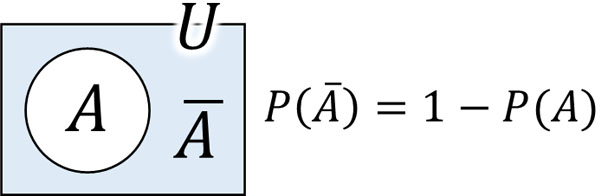
例えば工場で無造作に5つの製品を取り、少なくとも1つ不良品が検出される確率を求めるためには、「すべて不良品ではない確率」を計算すればいいとわかります。すべて不良品でない確率がわかれば、全事象から引くことによって、余事象（少なくとも1個は不良品が含まれる確率）を計算できます。

このように余事象の確率\(P(\overline{A})\)を計算するとき、事象Aの確率\(P(A)\)を計算しましょう。例えば、以下の問題の答えは何でしょうか。

• 白玉4つ、赤玉3つ、青玉2つが混ざっています。この中から無造作に3つの玉を取り出す場合、少なくとも白玉が1つ含まれる確率はいくらでしょうか？

少なくとも1つ白玉が含まれるということは、白玉がまったく含まれていない確率を計算すればいいです。その後、全事象から白玉が全く含まれない確率を引くことによって、少なくとも1つは白玉が含まれる確率を計算できます。

「白玉が1つ含まれる確率」「白玉が2つ含まれる確率」「白玉が3つ含まれる確率」をそれぞれ計算した後、足し算（加法定理）によって答えを出すこともできます。ただシンプルな計算をするためには余事象を利用しましょう。

玉は合計で9つなので、全事象は₉C₃です。また赤玉と青玉は合計で5つであり、この中から3つの玉を取り出せば、白玉が含まれない確率を計算できます。白玉が含まれないケースは₅C₃であるため、以下の計算式になります。

\(1-\displaystyle\frac{_5C_3}{_9C_3}=\displaystyle\frac{37}{42}\)

こうして、余事象を利用することによって計算をシンプルにできます。計算ミスを少なくするため、余事象を利用することによって確率の計算をしましょう。

確率の基本と性質を学んで計算する

確率の計算では、必ず全事象を計算しなければいけません。すべてのケースを計算した後、該当する事象が何通り起こるのか計算するのです。

ただ確率の計算では、複数の事象が起こるときの確率を計算しなければいけないことがあります。このとき排反事象については、足し算によって計算しましょう。加法定理により、足すことによってAまたはBが起こる確率を計算できます。

一方、AとBに重なる部分がある場合、和事象の確率を計算しましょう。Aの確率とBの確率を足した後、AとBが重なる部分（積事象）を引きます。これによって和事象の確率を計算できます。

また事象が起こる確率を計算することによって、余事象の確率を計算できます。余事象の確率を計算するほうが、計算式をシンプルにできることはよくあります。これら確率の性質と計算方法を理解し、確率を求めるようにしましょう。