図形と漸化式：交点や円、三角形の相似を利用する解き方

漸化式を利用することにより、図形の問題を解かなければいけないことがあります。以前の結果を利用して、新たな結果を得られる方法が漸化式です。そのため漸化式を利用する図形では、図形の数が増えていきます。

漸化式は解き方が決まっています。図形で漸化式を利用する場合であっても、解き方を知っていれば答えを得ることができますし、解き方を知らなければ答えを得るのは難しいです。

そのため図形で漸化式を利用するとき、事前に解答方法がわかるようになりましょう。解き方を予想せずに計算してはいけません。

それでは、図形と漸化式が組み合わさっている問題はどのように解けばいいのでしょうか。図形と漸化式について解説していきます。

1 図を描き、漸化式を利用して計算する
- 1.1 線と図形を利用する領域の個数に関する問題
- 1.2 接する図形と長さ・面積を計算する
2 図形を描き、漸化式を作る
- 2.1 相似を利用して一般項を得る
3 図形を作り、漸化式を作成する

図を描き、漸化式を利用して計算する

数学で図形の問題を解くとき、大まかにでもいいので、図を描くようにしましょう。そうしなければ、計算問題を解くのは難しいです。

漸化式では、図形が増えていきます。このとき $n=1$ 、 $n=2$ 、 $n=3$ のときの図形を描きましょう。そうすれば、図形と漸化式の関係を把握できます。

特に重要なのは、 $n=1$ の図形と $n=2$ の図形です。漸化式では、一つ前の結果を利用して計算することになります。そこで $n=1$ から $n=2$ へ変化するとき、個数や長さ、面積に着目することで式を作るのです。

このとき、図形と漸化式では以下の2パターンに分けることができます。

線と図形を利用する領域の個数
接する図形と長さ・面積

そこで、それぞれのパターンについて問題の解き方を学びましょう。

線と図形を利用する領域の個数に関する問題

線や円を利用することによって、漸化式に関する問題を解くケースがあります。線や円を増やすことにより、領域の数が増えます。まずは、線を利用する場合の領域数を確認していきましょう。

平面上に直線を $n$ 本引きます。それぞれの線が平行ではなく、交点で2本の線のみが交わる場合、 $n=1$ 、 $n=2$ 、 $n=3$ のときの図を以下のように作れます。

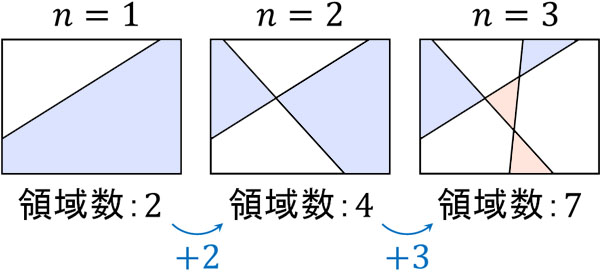
この結果から読み取れることは何でしょうか。直線の数が $n$ から $n+1$ に増えるとき、領域の数は $n+1$ 個増えます。そこで、この性質を利用して漸化式を作りましょう。領域数を $a_n$ とすると、以下の漸化式を作れます。

$a_{n+1}=a_n+(n+1)$

このように確認すると、なぜ図を描かないと式を作れないのか理解できると思います。なお条件によって領域の数は変化するため、必ず図を描くことで漸化式を作らなければいけません。

次に、円を増やす場合の領域数を確認していきましょう。一つの円がそれぞれの円と2点で交わり、3線以上で交わる交点が存在しない場合、以下のように $n=1$ 、 $n=2$ 、 $n=3$ のときの図を作れます。

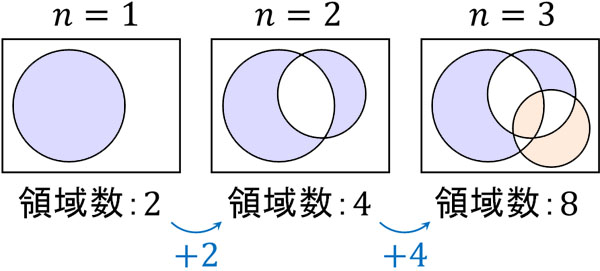
この場合、領域数 $a_n$ に対して $2n$ を加えると、新たな領域数 $a_{n+1}$ になります。そのため、以下の式を作れます。

$a_{n+1}=a_n+2n$

これが、線と図形を利用して領域の数を計算する方法です。

接する図形と長さ・面積を計算する

図形と漸化式に関する問題では、線の長さや図形の面積を計算しなければいけないケースもあります。線や円が互いに接するとき、線の長さや面積が問われます。このとき円と多角形では問題を解くときの方針が異なります。

円では、三平方の定理を利用することで2つの円の中心間の距離を計算しましょう。例えば以下の図について、円Aと円Bの半径をそれぞれ $r_a$ 、 $r_B$ とします。この場合、中心間の距離や三平方の定理を利用することにより、辺の長さがわかります。

また辺の長さがわかれば、三角形の面積を計算することもできます。一方で多角形では、相似を利用することで辺の長さや面積を計算することを考えましょう。

こうした方針を理解することにより、図形を利用して漸化式を作れるようになります。

図形を描き、漸化式を作る

それでは、実際に練習問題を解くことで一般項を計算できるようになりましょう。以下の問題の答えは何でしょうか。

平面上に直線を $n$ 本引きます。それぞれの線は平行ではなく、交点では2本の線のみが交わります。 $n$ 本の直線によって作られる交点の数を $a_n$ とするとき、 $a_n$ を $n$ の式で表しましょう。

まず、図を作ります。先ほど、直線を利用して領域の数を計算しました。ただ問題文では、領域の数ではなく交点の数が問われています。そこで、交点の数がどのように変化するのか確認しましょう。

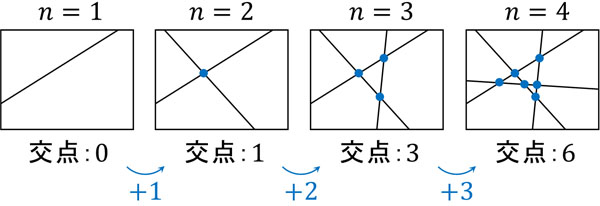
このように確認すると、 $n$ から $n+1$ へ変化するとき、交点の数 $a_n$ に対して $n$ を足す必要があるとわかります。そのため、漸化式を作ると以下のようになります。

$a_{n+1}=a_n+n$

$a_{n+1}-a_n=n$

こうして、階差数列型の漸化式を作ることができました。そこで、以下のように計算しましょう。

$a_n=a_1+\displaystyle\sum_{k=1}^{n-1}{k}$

$a_n=0+\displaystyle\frac{1}{2}(n-1)n$

$a_n=\displaystyle\frac{1}{2}(n-1)n$

なお $n=1$ を代入すると、 $a_1=\displaystyle\frac{1}{2}(1-1)·1$ $=0$ です。 $n=1$ のときも成り立つため、 $a_n=\displaystyle\frac{1}{2}(n-1)n$ です。

相似を利用して一般項を得る

図形と漸化式に関わるほかの練習問題を解いてみましょう。以下の問題の答えは何でしょうか。

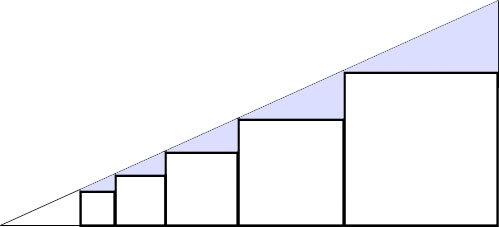
O $(0,0)$ 、A $(4,0)$ 、B $(4,2)$ を頂点とする三角形について、以下のように正方形を順に内接させます。 $n$ 番目の正方形について、一片の長さを $a_n$ 、面積を $S_n$ とします。数列 $\{a_n\}$ について漸化式を作成し、一般項を求めましょう。また、正方形の面積を $S_1$ から $S_n$ まで足すときの答えを計算しましょう。

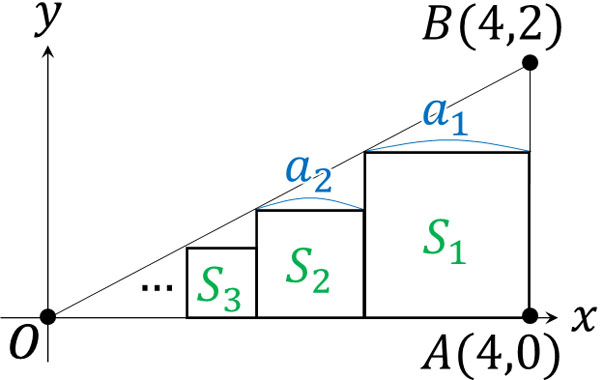
まず、初項 $a_1$ を計算しましょう。以下のように、三角形を利用して長さを記入します。

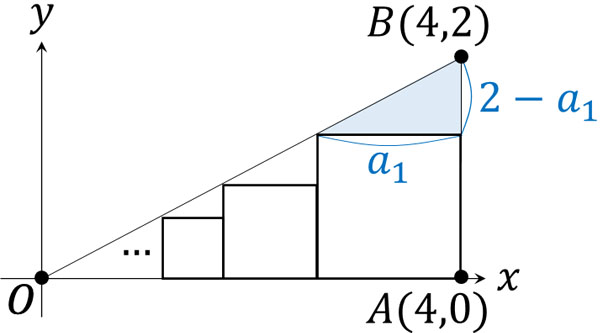
△OABと $a_1$ を底辺とする三角形は相似です。また $OA=4$ 、 $AB=2$ であるため、以下の計算をすることができます。

$4:2=a_1:2-a_1$

$2a_1=8-4a_1$

$6a_1=8$

$a_1=\displaystyle\frac{4}{3}$

こうして、初項を得ることができました。次に、 $a_n$ と $a_{n+1}$ に着目しましょう。図を作ると以下のようになります。

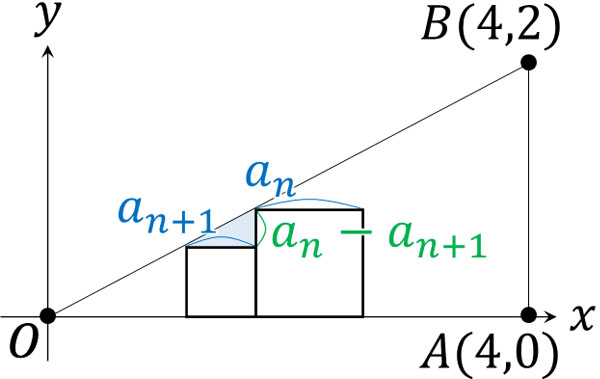
そこで、先ほどと同様に相似を利用して式を作ります。

$4:2=a_{n+1}:a_n-a_{n+1}$

$2a_{n+1}=4a_n-4a_{n+1}$

$6a_{n+1}=4a_n$

$a_{n+1}=\displaystyle\frac{2}{3}a_n$

こうして、数列 $\{a_n\}$ は初項 $\displaystyle\frac{4}{3}$ 、公比 $\displaystyle\frac{2}{3}$ の等比数列とわかります。そのため、一般項は以下になります。

$a_n=\displaystyle\frac{4}{3}·\left(\displaystyle\frac{2}{3}\right)^{n-1}$

一般項を得たら、次に面積の計算をしましょう。2つの辺をかければ面積を得ることができるため、 $S_n$ の一般項は以下になります。

$S_n=\displaystyle\frac{4}{3}·\left(\displaystyle\frac{2}{3}\right)^{n-1}$ $×\displaystyle\frac{4}{3}·\left(\displaystyle\frac{2}{3}\right)^{n-1}$

$S_n=\displaystyle\frac{16}{9}·\left(\displaystyle\frac{4}{9}\right)^{n-1}$

正方形の面積を $S_1$ から $S_n$ まで足すとき、計算は以下のようになります。

$\displaystyle\sum_{k=1}^{n}{S_k}$ $=\displaystyle\frac{\displaystyle\frac{16}{9}\left\{1-\left(\displaystyle\frac{4}{9}\right)^{n}\right\}}{1-\displaystyle\frac{4}{9}}$

$=\displaystyle\frac{16}{5}-\displaystyle\frac{16}{5}\left(\displaystyle\frac{4}{9}\right)^n$

こうして、面積を計算することができました。図を作り、相似を利用すれば計算できます。