集合と命題を学ぶとき、命題の証明をすることが頻繁にあります。一つの命題に対して、真なのか偽なのか確かめるのです。また真の場合、なぜその命題が正しいのか証明します。
証明をするとき、いくつか方法があります。最もわかりやすい方法としては、命題が正しいことを直接証明するやり方です。一方、対偶を利用して証明する方法もあります。そのため、命題の逆や裏、対偶が何かを理解しなければいけません。
または、背理法を用いて証明する方法も知られています。背理法では命題を否定します。その後、矛盾があるかどうかを探します。これによって証明するのが背理法です。
命題の真偽を判断するとき、複数の方法があります。そこで、どのように命題の証明をすればいいのか解説していきます。
もくじ
命題を証明する方法
一つの命題について、それが正しいかどうかを証明するためにはどのようにすればいいのでしょうか。証明する方法としては、直接的に証明する方法と間接的に証明する方法の2種類があります。最もわかりやすい証明方法が直接証明法です。
直接証明法では、なぜ命題が成り立つのか順に説明していきます。例えば、以下の命題の証明はどのようにすればいいのでしょうか。
- 整数\(n\)が偶数なら、\(n^2\)は偶数になる
この証明をするため、整数を\(n\)を\(2k\)としましょう。すべての偶数は2の倍数であるため、偶数は\(2k\)と表すことができます。そのため、\(n^2\)は以下のようになります。
\(n^2=(2k)^2=4k^2\)
\(4k^2\)は2の倍数です。そのため整数\(n\)が偶数なら、\(n^2\)は偶数になります。このように、命題が成り立つ理由を順に説明していきましょう。
命題が偽の場合、反例が存在する
一方で命題が偽のケースがあります。この場合、命題が偽である例(反例)を述べるようにしましょう。命題が成り立たない条件が1つでもある場合、その命題は偽です。
例えば、以下の命題が偽であることを証明するにはどうすればいいでしょうか。
- \(|a-2|>3\)ならば、\(a>5\)となる
\(|a-2|>3\)を解くと答えは\(a<-1,5<a\)となります。\(a<-1\)であっても成り立つため、先ほどの命題は偽です。このように命題が成り立たない条件を述べることによって、命題が偽であると証明することができます。
逆・裏・対偶の意味
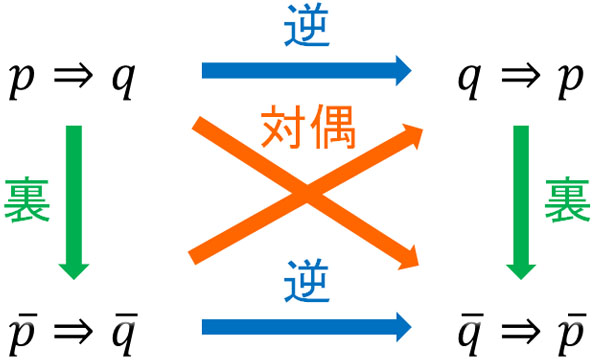
次に命題を間接的に証明する方法を学びましょう。その前に命題の逆や裏、対偶について理解しなければいけません。命題の逆や裏、対偶とは何なのでしょうか。命題\(p⇒q\)に対して、逆や裏、対偶はそれぞれ以下の関係になります。
- 逆:\(q⇒p\)
- 裏:\(\overline{p}⇒\overline{q}\)
- 対偶:\(\overline{q}⇒\overline{p}\)
例えば、以下の命題があるとします。
- \(x=3\)ならば、\(x^2=9\)
この命題の逆や裏、対偶はそれぞれ以下のようになります。
- 逆:\(x^2=9\)ならば、\(x=3\)
- 裏:\(x≠3\)ならば、\(x^2≠9\)
- 対偶:\(x^2≠9\)ならば、\(x≠3\)
それぞれ、このように変換できます。
命題とその対偶は真偽が一致する
それでは、なぜ集合と命題で逆や裏、対偶を学ぶことが重要になるのでしょうか。この理由として、対偶を利用することによって命題が正しかどうかを間接的に証明できるからです。より詳しくいうと、命題と対偶の真偽は一致します。
つまり命題が真の場合、その対偶は必ず真です。また命題が偽の場合、その対偶は必ず偽です。つまり対偶が真であることを証明すれば、その命題は真であると証明できます。
命題が真のとき、逆や裏は必ずしも真ではありません。先ほどの例であれば、以下の命題は偽です。
- 逆:\(x^2=9\)ならば、\(x=3\)
- 裏:\(x≠3\)ならば、\(x^2≠9\)
理由としては\(x=-3\)であっても成り立つからです。一方で対偶はどうでしょうか。
- 対偶:\(x^2≠9\)ならば、\(x≠3\)
\(x^2≠9\)の答えは\(x≠±3\)です。そのため\(x^2≠9\)ならば、必ず\(x≠3\)となります。そのため、対偶は真です。その理由については、pとqの集合をそれぞれPとQにするとき、以下の図によって説明できます。
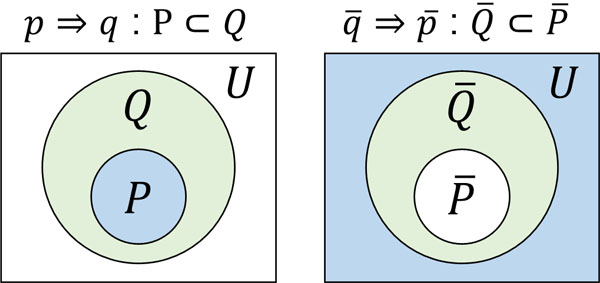
\(p⇒q\)のとき、必ず\(P⊂Q\)となります。QがPを含むからこそ、Pがどのような値であってもQも成り立ちます。
一方、\(\overline{q}⇒\overline{p}\)についてはどうでしょうか。図を確認すると、\(\overline{Q}⊂\overline{P}\)になっていることがわかります。つまり\(p⇒q\)が真のとき、\(\overline{P}\)は\(\overline{Q}\)を含んでいます。\(\overline{Q}\)は\(\overline{P}\)の一部であるため、\(\overline{Q}\)がどのような値であっても\(\overline{P}\)も成り立ちます。
そのため、\(p⇒q\)が真のとき、\(\overline{q}⇒\overline{p}\)は真です。ベン図を確認すると、命題が真の場合、必ず対偶も真になるとわかります。
対偶を用いて証明する
それでは、実際に対偶を用いて証明をしてみましょう。以下の証明はどのようにすればいいでしょうか。
- \(n^2\)が偶数なら、整数\(n\)は偶数になる
この命題の対偶は以下のようになります。
- 整数\(n\)が奇数なら、\(n^2\)は奇数になる
そこで、対偶が真であることを証明しましょう。整数\(n\)を\(2k+1\)とします。\(2k+1\)は必ず奇数になるからです。次に、\(n^2\)を計算しましょう。以下のようになります。
\(n^2\)
\(=(2k+1)^2\)
\(=4k^2+4k+1\)
\(=4k(k+1)+1\)
\(4k(k+1)\)は2倍数であるため、この式に1を加えると必ず奇数になります。そのため、\(4k(k+1)+1\)は奇数です。こうして、対偶が真であると証明できます。また対偶が真であるため、命題は真になります。
背理法を利用する証明
命題が真であることを間接的に証明する方法はほかにもあります。それが背理法です。対偶を利用しての証明が難しい場合、背理法を利用して証明することができます。背理法とは、矛盾を利用して証明する方法になります。
集合Aについて、背理法では否定をします。つまり、\(\overline{A}\)を確認します。仮に\(\overline{A}\)が正しい場合、\(\overline{A}\)は真でなければいけません。しかし\(\overline{A}\)に矛盾がある場合、\(\overline{A}\)は偽です。
そこで\(\overline{A}\)が誤りであることを証明すれば、Aは真となります。例えば、AとBの2つの箱があるとします。AまたはBのうち、どちらか一方にボールが入っています。

Aにボールが入っていることを証明するためには、Bにボールが入っていないことを証明すればいいです。この場合、Aの否定は\(\overline{A}\)です。また今回の例では\(\overline{A}=B\)です。そこで、Bにボールが入っていると仮定しましょう。ただBにボールが入っていないと判明した、内容は矛盾します。そのため、Bにボールが入っていることが否定されます。
集合B(\(\overline{A}\))が正しくないとわかったため、ボールはAに入っているとわかります。こうして、集合Aが正しいと説明できます。
このように集合Aを否定し、\(\overline{A}\)に着目します。その後、\(\overline{A}\)に矛盾を見つけることができれば、集合Aは真であると証明できます。これが背理法です。
実際に背理法によって証明する
それでは、実際に背理法を利用して集合が正しいことを証明しましょう。例えば、以下の命題を証明するにはどうすればいいでしょうか。
- \(\sqrt{2}+\sqrt{3}\)は無理数である。ただし、\(\sqrt{3}\)は無理数であると既に知られているものとする
実数には有理数と無理数があります。また\(\sqrt{2}+\sqrt{3}\)が無理数であることを直接証明するのは難しいです。そこで、間接的に証明する背理法を利用しましょう。
命題の反対を述べる必要があるため、以下のように変えます。
- \(\sqrt{2}+\sqrt{3}\)は有理数である
つまり\(\sqrt{2}+\sqrt{3}\)が有理数であることを否定できれば、\(\sqrt{2}+\sqrt{3}\)が無理数であることの証明になります。そこで、\(\sqrt{2}+\sqrt{3}=k\)としましょう。そうすると、以下のようになります。
\(\sqrt{2}+\sqrt{3}=k\)
\(\sqrt{2}=k-\sqrt{3}\)
両辺を二乗します。
\(2=k^2-2\sqrt{3}k+3\)
\(2\sqrt{3}k=k^2+1\)
\(k≠0\)である。
\(\sqrt{3}=\displaystyle\frac{k^2+1}{2k}\)
\(k\)は有理数であるため、\(k^2+1\)と\(2k\)は有理数です。そのため、右辺は有理数です。つまり、左辺も有理数になる必要があります。しかし、左辺にある\(\sqrt{3}\)は無理数であり、結果が矛盾します。したがって、\(\sqrt{2}+\sqrt{3}\)は無理数です。
このように背理法では、命題の逆を述べましょう。その後、命題の逆が矛盾することを証明できれば、命題が真であると証明できます。
命題の証明を行う
証明の問題は多くの人が嫌います。どのように証明すればいいのか理解しにくいからです。ただ、証明をするときは手順があります。
最もわかりやすい証明の方法として直接証明があります。命題が正しいことについて、理由を述べるようにしましょう。また命題が正しくない場合、反例を述べるようにしましょう。そうすれば、命題が偽であるとわかります。
また対偶や背理法を利用することによって、間接的に命題が真であると証明できます。解き方の手順を理解していないと証明できないため、対偶や背理法を用いた証明の方法を学びましょう。
集合と命題で証明をするとき、正しいやり方があります。そこで、証明の方法を理解するようにしましょう。