複素数平面で円を利用することは多いです。座標やベクトルで円を利用するのと同様に、複素数平面でも円を描けるようになりましょう。
複素数平面はベクトルと性質が似ているため、ベクトル方程式での円を理解している場合、複素数平面で円の方程式を学ぶのは難しくありません。
なお複素数平面では、アポロニウスの円も取り扱います。2つの点の内分点を利用することにより、円を得られるのです。また、式を確認することでどのような円を描くことができるのか判断できるようになりましょう。
それでは、複素数平面で円の方程式を利用して計算するにはどうすればいいのでしょうか。複素数平面での円の方程式やアポロニウスの円について解説していきます。
複素数平面での円の方程式
まず、複素数平面での円の方程式を確認しましょう。点A(複素数\(α\))が中心であり、半径\(r\)の円について、円上の点を\(z\)とすると、以下の式で表すことができます。
- \(|z-α|=r\)
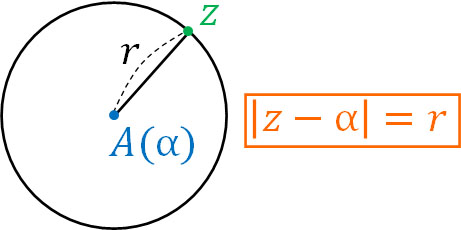
\(z\)と\(α\)の距離について、絶対値を用いて\(|z-α|\)と表すことができることをすでに学んでいると思います。\(z\)と\(α\)の距離は半径\(r\)になるため、この方程式が成り立つと問題なく理解できます。
複素数平面での円の方程式というのは、円のベクトル方程式と公式がほぼ同じです。ベクトル方程式と複素数平面で利用される方程式を対応して覚えましょう。
方程式を確認し、図形を描く
それでは、式を確認することで図形を描けるようになりましょう。以下の式はどのような図形を表しているでしょうか。
- \(\left|\displaystyle\frac{z-2-2i}{1-i}\right|=1\)
式を以下のように変形しましょう。
\(\left|\displaystyle\frac{z-2-2i}{1-i}\right|=1\)
\(\displaystyle\frac{|z-2-2i|}{|1-i|}=1\)
\(|z-2-2i|=|1-i|\)
\(|z-(2+2i)|=|1-i|\)
複素数平面での絶対値は原点との距離を表します。そのため\(|1-i|\)について、原点との距離は\(\sqrt{2}\)です。\(|1-i|=\sqrt{2}\)であるため、式は以下のようになります。
- \(|z-(2+2i)|=\sqrt{2}\)
つまり\(z\)は中心\(2+2i\)、半径\(\sqrt{2}\)の円を表します。
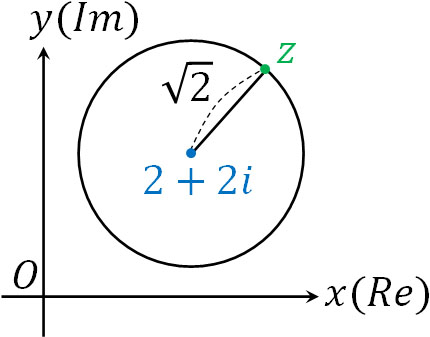
\(z\)は点であるものの、すべての\(z\)を集めると結果として円になるのです。
アポロニウスの円:複素数平面と内分点
次に、複素数平面でのアポロニウスの円を学びましょう。座標で円を習うとき、アポロニウスの円をすでに学んでいると思います。2つの点について、内分点(または外分点)をつなぐと円を作れます。これがアポロニウスの円です。
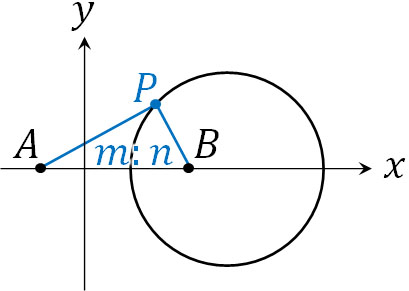
点A(複素数\(α\))と点B(複素数\(β\))について、2点からの距離が\(m:n\)(\(m≠n\))となる場合、以下の式によってアポロニウスの円を表現できます。
- \(n|z-α|=m|z-β|\)
前述の通り、絶対値と引き算を利用することによって複素数平面での距離を表すことができます。そのため点Aと\(z\)の距離は\(|z-α|\)であり、点Bと\(z\)の距離は\(|z-β|\)です。また\(z\)は2点からの距離が\(m:n\)となるため、以下の式を作れます。
\(|z-α|:|z-β|=m:n\)
\(n|z-α|=m|z-β|\)
こうして、先ほど記した複素数平面での方程式を得ることができました。なお、この円は線分ABの内分点と外分点が直径の両端となります。
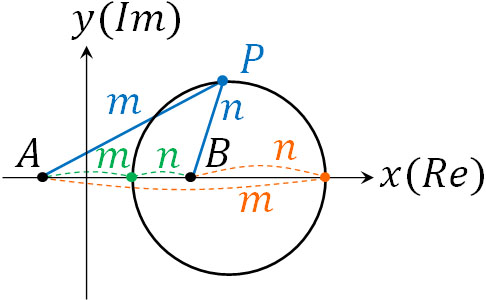
それでは、複素数平面でアポロニウスの円に関する問題を解きましょう。以下の問題の答えは何でしょうか。
- \(2|z+4i|=3|z-i|\)で表される\(z\)はどのような図形でしょうか。
両辺を二乗することによって計算しましょう。このとき、\(|z|^2=z\overline{z}\)を利用しましょう。
\(2|z+4i|=3|z-i|\)
\(4|z+4i|^2=9|z-i|^2\)
\(4(z+4i)(\overline{z+4i})\)\(=9(z-i)(\overline{z-i})\)
\(4(z+4i)(\overline{z}-4i)\)\(=9(z-i)(\overline{z}+i)\)
\(4(z\overline{z}-4zi+4\overline{z}i+16)\)\(=9(z\overline{z}+zi-\overline{z}i+1)\)
\(5z\overline{z}+25zi-25\overline{z}=55\)
\(z\overline{z}+5zi-5\overline{z}=11\)
\((z-5i)(\overline{z}+5i)-25=11\)
\((z-5i)(\overline{z-5i})=36\)
\(|z-5i|^2=36\)
\(|z-5i|=6\)
こうして、中心が\(5i\)である半径6の円であることがわかりました。
複素数の式を変形し、円の方程式を得る
それではここまで解説した知識を利用して、複素数の式を変形することで円の方程式を得られるようになりましょう。具体的には、\(w=αz+β\)によって表される図形を計算します。以下の問題の答えは何でしょうか。
- 点\(z\)が2を中心とする半径1の円上を動くとき、\(w=(1+i)z-i\)で表される点\(w\)はどのような図形を描くでしょうか。
点\(z\)は2を中心とする半径1の円上を動くため、\(|z-2|=1\)と表すことができます。そこで、\(w=(1+i)z-i\)を以下のように変形しましょう。
\(w=(1+i)z-i\)
\((1+i)z=w+i\)
\(z=\displaystyle\frac{w+i}{1+i}\)
そこで、\(z=\displaystyle\frac{w+i}{1+i}\)を\(|z-2|=1\)に代入しましょう。
\(|z-2|=1\)
\(\left|\displaystyle\frac{w+i}{1+i}-2\right|=1\)
\(\left|\displaystyle\frac{w-2-i}{1+i}\right|=1\)
\(\displaystyle\frac{|w-2-i|}{|1+i|}=1\)
\(|w-2-i|=|1+i|\)
\(|w-(2+i)|=\sqrt{2}\)
そのため点\(w\)が描く図形は中心が\(2+i\)、半径\(\sqrt{2}\)の円とわかります。式を作った後、問題文の式に代入することによって点\(w\)がどのような図形であるのか把握できます。
複素数平面で利用される円の方程式を学ぶ
円のベクトル方程式と複素数平面での円の方程式はほぼ同じです。そのため円のベクトル方程式を学んでいる場合、複素数平面で学ぶ円の方程式は新たな概念ではありません。
なお複素数平面で円の方程式を利用するとき、必ず絶対値を利用することになります。そこで、複素数での絶対値(距離)が何を意味しているのか事前に学んでおく必要があります。また、絶対値を含む複素数の計算を行うことで答えを得ましょう。
また、複素数平面ではアポロニウスの円を計算することがあります。アポロニウスの円では、内分点と外分点を結ぶと円の直径になります。こうした性質があることを学びましょう。
式を確認することにより、円を描けるようになることが重要です。円の方程式と複素数平面を関連付けて計算できるようになりましょう。






