楽器からなぜ音が鳴るかというと、波が振動することによって定常波を生じるからです。そのため物理で波動を学べば、楽器の原理を理解できます。
楽器の中でも、トランペットやフルートなどの管楽器では、管の長さを調節したり、穴をふさいだりすることで音を調節します。それでは、なぜこうした操作によって生じる音が変わるのでしょうか。
またビンに息を吹きかけることによって、音を出すことができます。空気が振動することによって共鳴し、音が鳴るのです。このときビンとフルートでは、音が鳴るときの仕組みが異なります。そこで、どのような違いがあるのか理解しましょう。
閉管なのか開管なのかによって、気柱(管の内部にある空気)に生じる定常波の様子が異なります。そこで、どのような条件で音を生じるのか解説していきます。
もくじ
気柱の共鳴と定常波:閉管での固有振動
まず、片側が閉じている管(閉管)で音が鳴る場面を考えていきましょう。ビンの口に横から息を吹きかけることにより、音が鳴ります。誰でも、一度は試してみたことがあると思います。空気が共鳴することにより、音を生じるのです。
ビンは片方が開いており、一方が閉まっています。このような管を閉管(へいかん)といいます。
ただ、息を吹きかけることによって音を鳴らすにしても、息の強さや角度が正しくなければ音はなりません。気柱に定常波が生まれ、共鳴しないと音はならないのです。それでは音が鳴っているとき、気柱に生じる定常波はどのような状態になっているのでしょうか。
ビンの口が開いている場合、空気は自由に動くことができるので自由端反射になります。一方でビンの底は壁となっており、空気は自由に動くことができません。そのため、固定端反射となります。
一方が自由端反射で一方が固定端反射であるため、定常波を作るとき、閉管での基本振動(最も単純な定常波)は以下のようになります。
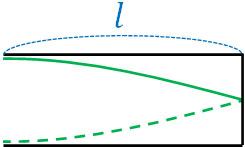
このように基本振動では、\(\displaystyle\frac{λ}{4}\)のとき(波長の4分の1のとき)、管の長さ\(l\)と等しくなります。つまり、\(l=\displaystyle\frac{λ}{4}\)となります。
基本振動の数が奇数のとき、閉管では音が鳴る
なお閉管の場合、2倍振動や4倍振動は存在しません。必ず基本振動の奇数倍となります。この理由として、一方が自由端反射であり、もう一方が固定端反射だからです。この条件を満たすように定常波を作る場合、2倍振動や4倍振動を作ることはできません。
管の一方が閉管であると、基本振動以外では、以下のように3倍振動や5倍振動となります。
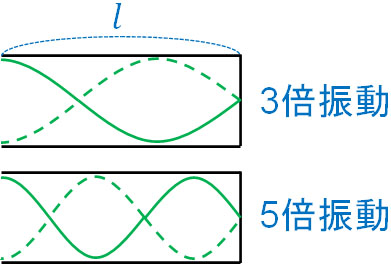
なお図より、管の長さ\(l\)と波長\(λ\)の関係はそれぞれ以下のようになります。
- 基本振動:\(l=\displaystyle\frac{λ}{4}\)
- 3倍振動:\(l=\displaystyle\frac{3λ}{4}\)
- 5倍振動:\(l=\displaystyle\frac{5λ}{4}\)
3倍振動では、\(\displaystyle\frac{λ}{4}\)が3つあります。また5倍振動では、\(\displaystyle\frac{λ}{4}\)が5つあります。そのため、上記の式を作れます。
式を確認すると、基本振動を奇数倍することによって定常波が作られるとわかります。なお、基本振動に対して奇数倍であればいいため、7倍振動や9倍振動を作ることもできます。
管の長さや波長、速さ、振動数の関係
次に、管の長さ\(l\)と波長\(λ\)の関係を利用することで、速さ\(v\)と振動数\(f\)を利用する式を作りましょう。
波の公式より、\(v=fλ\)です。つまり、\(λ=\displaystyle\frac{v}{f}\)です。そこで、基本振動を表す\(l=\displaystyle\frac{λ}{4}\)に代入しましょう。以下のようになります。
- 基本振動:\(l=\displaystyle\frac{v}{4l}\)
こうして、基本振動の固有振動数は\(f=\displaystyle\frac{v}{lf}\)になるとわかります。同様に3倍振動や5倍振動の固有振動数を計算すると以下のようになります。
- 3倍振動:\(f=\displaystyle\frac{3v}{l}\)
- 5倍振動:\(f=\displaystyle\frac{5v}{l}\)
このように、固有振動数は奇数倍で増えていきます。式は異なるものの、振動数を求める方法は弦に生じる定常波と同じなので難しくないです。
開管となっている気柱での定常波
次に閉管ではなく、入り口と出口の両方が開いている管で音が鳴る仕組みを理解しましょう。例えばリコーダーやフルートなどの楽器が該当します。
管楽器では、空気が振動・共鳴することによって音が出ます。このとき、リコーダーやフルートなどの管楽器では、両端が開いています。このような管を開管(かいかん)といいます。
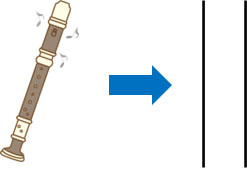
気柱の振動で重要なのは、振動は管の外に出ていかないことです。管の中と外では圧力差があり、大気圧によって振動は押し返されます。

こうして入射波と反射波が重なり、定常波が作られることによって音が鳴ります。
なお開管となっている場合、両端が開いているので自由端反射をします。つまり気柱に生じる定常波は両端が必ず腹になります。両端が腹になるとき、最も単純な定常波(基本振動)は以下になります。
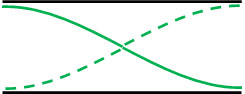
同様に、両端が腹になるように定常波を作る場合、以下のケースを考えることができます。
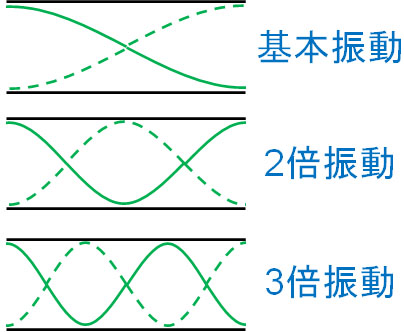
閉管の場合、基本振動を奇数個用いることによって定常波を作ることができました。一方で開管の場合、基本振動を2個や3個に増やすことにより、両端が腹になる定常波を作れます。そのため、管が開管の場合は2倍振動や3倍振動の定常波を作れます。
なおほかにも、4倍振動や5倍振動と続いていきます。
開管での管の長さ、波長、速さ、振動数の関係
それでは管が開管の場合について、管の長さ\(l\)と波長\(λ\)の関係を計算しましょう。先ほどの図より、基本振動の管の長さは\(\displaystyle\frac{λ}{2}\)です。基本振動では、管の長さ\(l\)と波長の半分が同じです。そのため、\(l=\displaystyle\frac{λ}{2}\)です。
同様に、2倍振動や3倍振動でも計算しましょう。そうすると、以下のようになります。
- 基本振動:\(l=\displaystyle\frac{λ}{2}\)
- 2倍振動:\(l=λ\)
- 3倍振動:\(l=\displaystyle\frac{3λ}{2}\)
2倍振動では、\(\displaystyle\frac{λ}{2}\)が2つあります。また3倍振動では、\(\displaystyle\frac{λ}{2}\)が3つあります。そのため、上記の式を作れます。
・速さと振動数を利用して式を作る
次に、先ほど得た式について、速さと振動数を用いて表しましょう。波の公式より、\(v=fλ\)であるため、\(λ=\displaystyle\frac{v}{f}\)です。そこで、\(λ=\displaystyle\frac{v}{f}\)を代入します。
- 基本振動:\(l=\displaystyle\frac{v}{2f}\)
- 2倍振動:\(l=\displaystyle\frac{v}{f}\)
- 3倍振動:\(l=\displaystyle\frac{3v}{2f}\)
これらの式を以下のように変換しましょう。
- 基本振動:\(f=\displaystyle\frac{v}{2l}\)
- 2倍振動:\(f=\displaystyle\frac{v}{l}\)
- 3倍振動:\(f=\displaystyle\frac{3v}{2l}\)
こうして、振動数を得る式を導き出すことができました。なお前述の通り、気柱に生じる定常波では、音の正体は空気による振動です。つまり空気を伝わる速さが重要であり、速さ\(v\)は音速です。管楽器の種類に関係なく音速は一定です。そのため、管楽器の振動数は管の長さのみに依存します。
弦に生じる定常波の式と比較して、先ほどの式は似ています。ただ弦での速さ\(v\)というのは、弦を伝わる波の速さであり、音速ではありません。弦の密度によって波の速さが異なるのです。一方で管の場合、管は振動せず、振動するのは空気です。そのため速さ\(v\)が一定になるのです。
穴の位置によって管楽器の音が変化する理由
管の長さによって振動数が変化するため、管楽器はどれも管の長さを調節することによって音が変化する仕組みになっています。
例えばリコーダーやフルートでは、管に穴が開いています。すべての穴をふさぐ場合、管は長くなります。一方で穴を開ける場合、穴の部分に大気圧による壁が発生します。つまり、穴が開いている部分で自由端反射が起こります。言い換えると、管が短くなります。

物理的に管を短くすることはできません。しかし、穴を利用することによって大気圧による壁を作り、結果として振動数を高くすることができるのです。
また、先ほどの式を再び確認しましょう。
- 基本振動:\(f=\displaystyle\frac{v}{2l}\)
管の長さ\(l\)が分母にあるため、管が長いほど振動数\(f\)は小さい値になります。言い換えると、管が長いほど低い音になります。管楽器で穴をふさぎ、管を長くするとすべての楽器で低い音が出るのはこうした理由があるのです。
気柱の共鳴で生じる開口端補正とは何か
なお気柱に生じる定常波を計算するとき、開口端補正を考慮するケースがあります。開口端補正とは何なのでしょうか。
先ほど、閉管や開管の場合、口が開いている場所では自由端反射を起こすと解説しました。これにより、定常波を生じて共鳴することで音が発生します。言い換えると、自由端反射を起こす場所では定常波の腹を生じます。
ただ実際には、定常波の腹ができるのは、管の口よりも少し外側です。この誤差を開口端補正といいます。
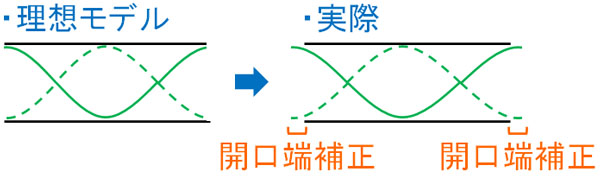
管が開管の場合、2ヵ所で開口端補正を生じます。それに対して管が閉管の場合、1カ所で開口端補正を生じます。
問題文によっては、開口端補正を考慮しなければいけないことがあります。そのため気柱に生じる定常波に関する問題を解くとき、開口端補正を無視するのか、それとも考慮するのか確認しましょう。
気柱に生じる定常波に関する練習問題
それでは、気柱に生じる定常波に関する物理の練習問題を解いてみましょう。以下の問題の答えは何でしょうか。
- 長さ\(l\)の管の左端に音源を置き、振動数\(f\)で音を出します。厚さを無視できるピストンを音源から右へ移動させると、距離\(d\)で初めて共鳴が起こり、右端で2回目の共鳴が起こりました。なお、開口端補正は考慮します。
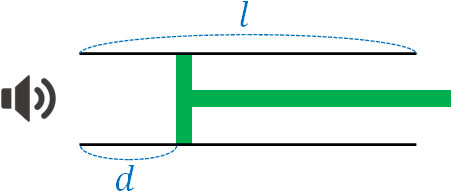
- 音波の波長を求めましょう。
- 音速を求めましょう。
- 開口端補正を求めましょう。
1) 音波の波長を求めましょう
開口端補正を考慮して計算する必要があります。距離\(d\)で基本振動が起こり、距離\(l\)で3倍振動が起こるため、以下の図を作ることができます。
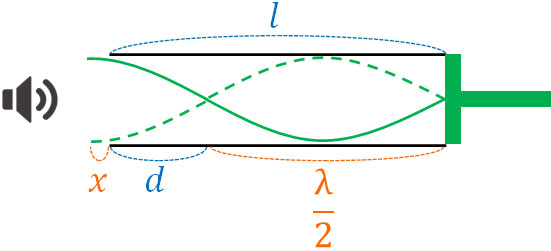
開口端補正の長さを\(x\)とし、開口端補正を考慮すると、これまで説明した方法では管の長さと波長を利用した関係式を作ることができません。
ただ上図より、\(l-d\)によって音波の半波長\(\displaystyle\frac{λ}{2}\)を得られることがわかります。そこで、以下の式を作りましょう。
\(l-d=\displaystyle\frac{λ}{2}\)
\(λ=2(l-d)\)
こうして、波長は\(λ=2(l-d)\)とわかりました。
2) 音速を求めましょう
\(v=fλ\)より、\(λ=\displaystyle\frac{v}{f}\)です。そこで、\(λ=\displaystyle\frac{v}{f}\)を\(λ=2(l-d)\)に代入しましょう。
\(λ=2(l-d)\)
\(\displaystyle\frac{v}{f}=2(l-d)\)
\(v=2f(l-d)\)
音速は\(v=2f(l-d)\)になると計算することができました。
3) 開口端補正を求めましょう
図より、\(x+d=\displaystyle\frac{λ}{4}\)です。そこで、\(λ=2(l-d)\)を代入しましょう。
\(x+d=\displaystyle\frac{λ}{4}\)
\(x+d=\displaystyle\frac{2(l-d)}{4}\)
\(x=\displaystyle\frac{l-3d}{2}\)
こうして、開口端補正は\(x=\displaystyle\frac{l-3d}{2}\)であると計算できました。
気柱に生じる定常波の計算問題を解けるようにする
波による影響によって音が聞こえます。管楽器で音が鳴るのは、空気が振動・共鳴するからなのです。そこで、どのような原理によって気柱に定常波が生まれ、音を生じるのか理解しましょう。
管には閉管と開管があり、定常波の様子はそれぞれ異なります。閉管の場合、定常波を生じるときは必ず奇数倍になります。一方、開管の場合は両端が自由端反射となるため、基本振動の\(n\)倍となります。
なお管を利用して音を鳴らす場合、実際には開口端補正が発生します。そのため気柱に発生する定常波に関する問題を解くとき、開口端補正を考慮する必要があるかどうかを確認しましょう。
波動で気柱に生じる定常波を学べば、管楽器の仕組みを理解できます。管楽器で音が出る仕組みや音色が変わる理由は数式を確認することで把握できるのです。