電流の大きさを測定できる機器に電流計があります。また、電圧(電位差)を測定できる機器に電圧計があります。
電流計と電圧計には、正しいつなぎ方が存在します。そこでこれらの機器について、なぜ直列または並列でつなぐ必要があるのか学びましょう。また電流計と電圧計には内部抵抗があります。電流計や電圧計を利用するとき、内部抵抗が測定値に対してどのように影響するのか理解する必要があります。
なお内部抵抗を利用することにより、本来よりも高い値を測定できるようになります。電流計では分流器を利用し、電圧計では倍率器を利用します。
それでは、どのように電流計や電圧計を利用すればいいのでしょうか。電流計・電圧計の利用法や計算方法を解説していきます。
もくじ
電流計のつなぎ方:直列接続でつなぐ
まず、電流計を確認しましょう。電気回路につなぐとき、直接接続と並列接続の2種類があります。電流を測るとき、直接接続と並列接続のどちらが正しいでしょうか。
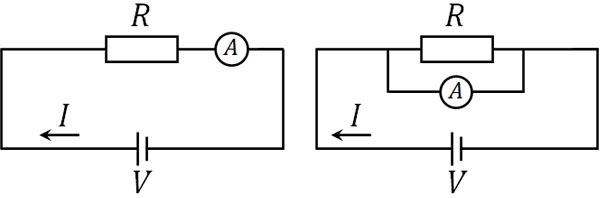
答えをいうと、電流計は直列接続でなければいけません。それでは、なぜ電流計では直列接続を利用するのでしょうか。物理では答えや公式を覚えても意味がないため、必ず理由を理解しましょう。
回路に枝分かれがあると、電流は必ず分かれます。つまり、以下の関係があるのです。
- \(I=I_1+I_2\)

この法則をキルヒホッフの第一法則といいます。つまり電流計を並列で接続すると、電流が枝分かれします。そのため、正確な電流量を測定できません。一方で直列接続であれば、電流が枝分かれすることなく、すべての電流が電流計に流入します。そのため、電流計は必ず直列接続となります。
このとき、測定したい場所に電流計を置きましょう。例えば下図で点Pを流れる電流の大きさを知りたい場合、点Aに電流計を置きます。
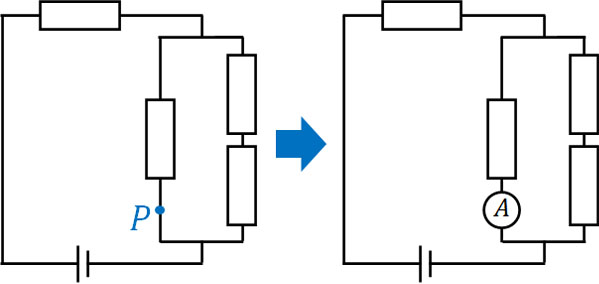
このようにして電流計を利用しましょう。
電流計では内部抵抗を小さくする
なお電流計では、電流計による内部抵抗をできるだけ小さくするほど測定結果が正確になります。要は、電流計による影響が少ないほどいいです。
電流計による内部抵抗が存在するというのは、例えば下図について、直列接続で2つの抵抗が存在することを意味します。
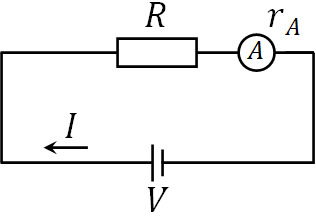
この図では、電源の起電力は\(V\)、電流は\(I\)、抵抗は\(R\)、電流計による内部抵抗は\(r_A\)です。そこでオームの法則を利用し、式を作ると以下のようになります。
\(V=RI+r_AI\)
\(V=I(R+r_A)\)
式を見てわかる通り、内部抵抗\(r_A\)が大きいと、電流\(I\)の値が小さくなってしまいます。これが、電流計で内部抵抗\(r_A\)を小さくする理由です。
電流計を利用しない場合、本来の値は\(V=RI\)になります。そこで先ほどの式について、内部抵抗\(r_A\)の値を極限まで小さくする場面を考えてみましょう。以下のようになります。
\(V=\displaystyle \lim_{ r_A \to 0 } I(R+r_A)\)
\(V=RI\)
内部抵抗\(r_A\)の値を極限まで小さくする場合、\(\displaystyle \lim_{ r_A \to 0 } r_A=0\)であるため、\(V=RI\)となります。このように数式からも、内部抵抗を小さくすると電流の大きさを正確に測定できることがわかります。
分流器を利用し、測定可能な電流の範囲を広げる
なお、電流計で測定できる電流の大きさには限界があります。それでは、より大きな電流を測定するにはどうすればいいのでしょうか。
電流の大きさを測定するとき、分流器を利用することによって、本来よりも大きい\(n\)倍の電流を測定できるようになります。
より正確にいうと、分流器を利用すると、電流計に流れる電流の量を\(\displaystyle\frac{1}{n}\)倍にできます。そこで電流計を使用して得た値に対して、\(n\)倍することで電流の大きさを測定するのです。
それでは、どのように分流器を利用すればいいのでしょうか。また、電流計に流れる電流量を\(\displaystyle\frac{1}{n}\)倍にするにはどうすればいいのでしょうか。
前述の通り、分流器には電流計に流れる電流量を少なくする役割があります。そこで、分流器を並列接続させましょう。並列接続であれば、電流を分流器に流すことができます。

このとき、分流器の抵抗によって、どれだけの電流が分流器に流れるのかが異なります。例として、電流\(I\)を\(n\)倍した\(nl\)の電流を流す場面を考えましょう。
回路全体の電流は\(nl\)[A]であり、電流計に\(l\)[A]の電流が流れる場合、分流器には\((n-1)l\)[A]の電流が流れます。

このとき、分流器と電流計は並列接続であるため、電位差(電圧降下の大きさ)は同じです。そこで電流計の抵抗を\(r_A\)、分流器の抵抗を\(R\)とすると、オームの法則より以下の式を作ることができます。
\(R(n-1)l=r_AI\)
\(R=\displaystyle\frac{r_A}{(n-1)}\)
つまり分流器の抵抗が\(R=\displaystyle\frac{r_A}{(n-1)}\)であれば、回路に存在する電流の合計\(nl\)[A]は電流計に\(l\)[A]流れます。つまり、電流計に流れる電流の大きさを\(\displaystyle\frac{1}{n}\)倍にすることができます。
分流器を利用する場合、抵抗の大きさを事前に計算する必要があります。抵抗の大きさにより、電流計に流れる電流の量が異なるからです。そこで、分流器で利用する抵抗の大きさをどのように計算すればいいのか理解しましょう。
電圧計のつなぎ方:内部抵抗を大きくする
次に電圧計を確認していきます。電圧計では、直列接続と並列接続のどちらを利用すればいいのでしょうか。
電位差を確認するために利用する機器が電圧計です。直列接続では、2ヵ所の電圧の差がわかりません。一方で並列接続であれば、接続した部分の2ヵ所でどれだけの電位差を生じているのかわかります。そのため、電圧計は必ず並列接続となります。
なお、電位差を調べたい場所に電圧計を設置しましょう。例えば、下図でAとBの間の電位差を知りたい場合、電圧計を利用してAとBをつなぎます。
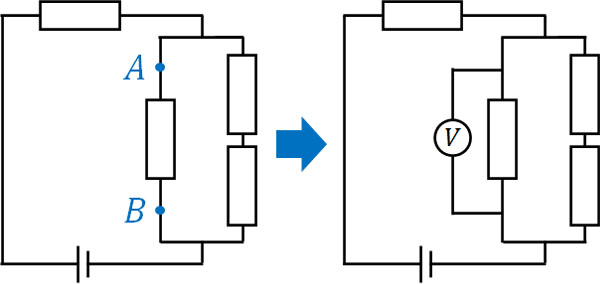
電流計とは異なり、電圧計では並列接続になることを理解しましょう。
電圧計で内部抵抗を大きくする理由
なお前述の通り、電流計では内部抵抗が小さいほど誤差が少なくなります。一方で電圧計では、内部抵抗が大きいほど誤差が小さくなります。つまり、電圧計の内部抵抗は大きいほどいいです。この理由は何でしょうか。
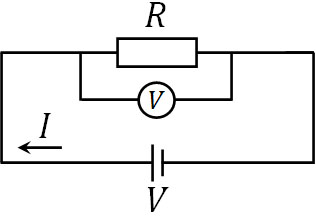
電圧計は並列接続されているため、電圧計の内部抵抗が小さい場合、電流は電圧計に流れます。ただ電圧計に電流が流れると、当然ながら正確な電圧を測定することはできません。そのため電圧計の内部抵抗を大きくすることで、電圧計に流れる電流を可能な限り少なくする必要があります。
例えば下図のように、電位差(電圧)\(V\)、電流\(I\)、抵抗\(R\)、電圧計による内部抵抗\(r_A\)で回路を作る場面を考えましょう。
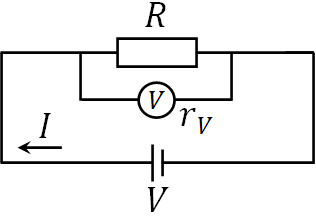
抵抗\(R\)と内部抵抗\(r_V\)の合成抵抗\(R’\)を計算すると以下のようになります。
\(\displaystyle\frac{1}{R’}=\displaystyle\frac{1}{R}+\displaystyle\frac{1}{r_V}\)
\(\displaystyle\frac{1}{R’}=\displaystyle\frac{R+r_V}{R·r_V}\)
\(R’=\displaystyle\frac{R·r_V}{R+r_V}\)
次に、オームの法則と合成抵抗\(R’=\displaystyle\frac{R·r_V}{R+r_V}\)を利用して式を作りましょう。
\(V=\displaystyle\frac{R·r_V}{R+r_V}I\)
正確な電圧を測定できる場合、\(V=RI\)となります。そこで、内部抵抗\(r_V\)を無限大まで大きくしましょう。以下のようになります。
\(V=\displaystyle \lim_{ r_V\to \infty } \displaystyle\frac{R·r_V}{R+r_V}I\)
\(V=\displaystyle \lim_{ r_V \to \infty } \displaystyle\frac{R}{\displaystyle\frac{R}{r_V}+1}I\)
\(V=RI\)
こうして、電圧計の内部抵抗が無限大に大きいとき、\(V=RI\)となるとわかりました。計算式によっても、電圧計の内部抵抗が大きいほど測定値が正確になるとわかります。
倍率器を利用し、\(n\)倍の電圧を測定する
なお電流計で分流器を利用できるのと同じように、電圧計についても、本来の能力の何倍もの電圧を測定できます。そのために必要な装置に倍率器があります。倍率器を利用することにより、本来よりも\(n\)倍の電圧を測定できるようになります。
原理は分流器と同じです。つまり\(n\)倍の電圧を測定したい場合、倍率器を利用することにより、電圧計に加わる電圧を\(\displaystyle\frac{1}{n}\)倍にすることができます。そのため倍率器を利用する場合、電圧計の測定値に対して、\(n\)倍することによって実際の値を得ます。
このとき、電圧計に対して倍率器を直列につなぎます。並列に抵抗(倍率器)をつなげても、電位差は同じです。電圧計と倍率器を直列接続することにより、電圧計に加わる電圧を和らげるのです。
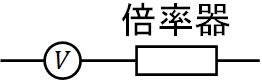
それでは、倍率器の抵抗をどのように調節すればいいのでしょうか。電位差\(V\)を\(n\)倍することで、全体の電位差(電圧)が\(nV\)となる場面を考えましょう。
全体の電位差が\(nV\)であり、電圧計に加わる電圧が\(V\)の場合、倍率器に加わる電圧は\((n-1)V\)です。
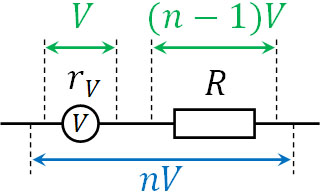
このとき、電圧計と倍率器は直列接続であるため、電流の値は同じです。オームの法則より、\(V=RI\)であるため、\(I=\displaystyle\frac{V}{R}\)です。そこで、以下の式を作りましょう。
\(\displaystyle\frac{V}{r_V}=\displaystyle\frac{(n-1)V}{R}\)
\(R=(n-1)r_V\)
つまり倍率器の抵抗が\(R=(n-1)r_V\)であり、全体の電位差\(nV\)のとき、電圧計に加わる電圧は\(V\)となります。言い換えると、倍率器の抵抗が\(R=(n-1)r_V\)であれば、電圧計に加わる電圧は\(\displaystyle\frac{1}{n}\)倍になります。また測定結果を\(n\)倍すれば、実際の電圧になります。
分流器と同じように、倍率器についても答えを覚えても意味がありません。そこで、どのように計算すればいいのか理解しましょう。
電流計・電圧計の利用法を学ぶ
電流の大きさを知りたい場合、電流計を利用します。回路に電流計を直列接続することによって、電流の大きさを測定できます。それに対して電圧では、2点の電位差を測定します。そのため、電圧計は並列接続となります。
このとき問題になるのが内部抵抗です。電流計と電圧計の両方とも内部抵抗が存在します。そこで、内部抵抗の値によって誤差がどのように変化するのか計算できるようになりましょう。
また電流計では分流器、電圧計では倍率器を利用することがあります。これらの装置を利用すれば、本来よりも大きい値を測定できます。そこで装置の原理や利用する抵抗の計算方法を理解しましょう。結果を覚えるのではなく、原理や問題の解き方を学ばなければいけません。
電流や電圧を測定するとき、測定方法や内部抵抗、分流器・倍率器の原理を理解しましょう。これにより、正しく電流と電圧の大きさを得られるようになります。






