波の干渉条件にはさまざまなパターンがあります。2つの波が強め合ったり、弱め合ったりするとき、それぞれのパターンを理解しなければいけません。
光は波の一種であり、重要な内容に薄膜での干渉条件があります。子供のとき、多くの人がシャボン玉を利用して遊んだことがあると思います。それでは、なぜシャボン玉は虹色に見えるのでしょうか。また水の上に浮かんでいる油はなぜ、光を反射することで虹色に見えるのでしょうか。
これらは薄膜で光が反射することによって起こる現象です。光が屈折し、強め合うことによって色が変化するのです。
薄膜での干渉を理解するためには、光学距離と反射による波の位相のずれを学ぶ必要があります。そこで、どのように薄膜での干渉を計算すればいいのか解説していきます。
もくじ
光学距離と反射による波の位相のずれ
薄膜での干渉を学ぶとき、事前に理解しなければいけない知識があります。それが光学距離と反射による波の位相のずれです。
光は空気中以外にも、水中やガラスについても進みます。このとき、媒質(空気中、水中、ガラスなど)によって光が進む速さは異なります。波長が変化することにより、水中などでは空気中よりも光のスピードは遅くなるのです。
例えば屈折率2の媒質では、光のスピードは真空中に比べて\(\displaystyle\frac{1}{2}\)倍となり、速さは遅くなります。ただ媒質によって速さが違う場合、計算が大変です。そこで異なる媒質を進む光について、真空中を進む距離に換算して計算しましょう。これを光学距離といいます。
屈折率\(n\)の媒質を進む場合、光の速さは\(\displaystyle\frac{1}{n}\)倍になります。そのため仮に真空中を進む場合、速さは\(n\)倍になります。例えば屈折率\(n\)の媒質について、距離\(l\)を進んだのであれば、真空中では\(nl\)を進むことになります。つまり、光学距離は\(nl\)です。
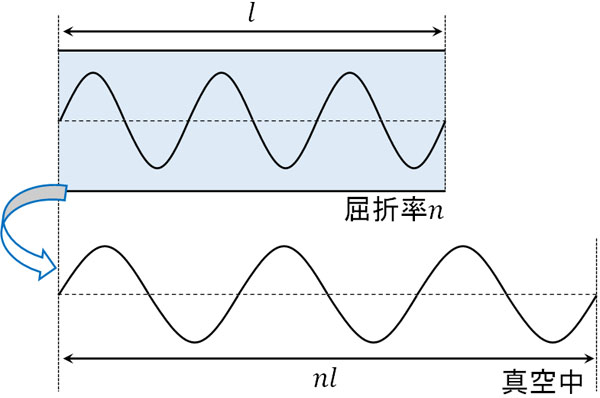
光が薄膜の中を進む場合、光学距離を考慮する必要があります。
自由端反射と固定端反射による位相のずれ
もう一つ学ばなければいけない事前知識が反射による位相のずれです。波が反射するとき、自由端反射と固定端反射のニ種類があります。自由端反射であれば位相に違いがありません。一方で固定端反射をする場合は位相が逆になります。
より具体的には、屈折率の小さい媒質(真空中など)を進んでいる光について、屈折率の大きい媒質で反射する場合、固定端反射となって逆位相になります。例えば空気と水の境目で光が反射する場合、空気中(屈折率1)のほうが屈折率は小さいので反射した光は逆位相になります。
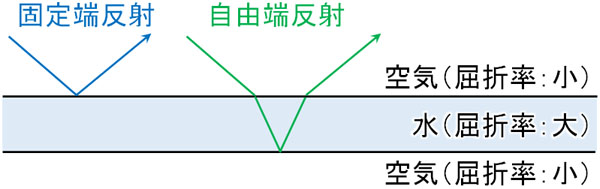
イメージとしては、固定端は振動しにくいです。屈折率が大きい物質では、波が伝わりにくいです(波の伝わるスピードが遅い)。これはつまり、波が振動しにくいことを意味しています。
そのため非常に短い時間で考えると、屈折率の大きい物質で光が反射するとき、屈折率の大きい物質を固定された壁と捉えることができます。端が固定されている壁で反射(固定端反射)することにより、波の位相が逆転するのです。
空気中を進む光は屈折率が低く、真空中と同様に屈折率はほぼ1です。そのため空気中を進んでいる光が水やガラスなどで反射する場合、位相がずれます。一方、屈折率の大きい媒質から屈折率の小さい媒質(ガラスから空気など)での光の反射は自由端反射となり、位相のずれは起こりません。
薄膜での距離の差(経路差)と光路差を計算する
ここまでの知識を利用して、薄膜での距離の差(経路差)を計算しましょう。薄膜での反射では、薄膜の下面で反射した光1と薄膜の上面で反射した光2によって干渉が起こります。空気中は真空中と同様に屈折率1で考えることができます。それに対して、薄膜の屈折率を\(n\)としましょう。
このとき、以下の図を作ることができます。
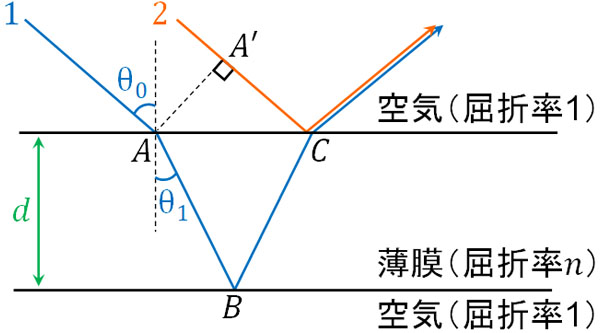
よくある間違いとして、経路差を得るとき、上図での距離の差を計算してしまうことがあります。つまり、以下の計算をしてしまうのです。
- \(AB+BC-A’C\)
ただ、この計算は誤りです。なぜ、この計算が間違いなのでしょうか。
薄膜へ光が入るタイミングを考慮する
光1が薄膜へ入ると、光が進む速さは遅くなります。そこで、光が屈折するときの図を作りましょう。以下の図を作ると、光2が点Cに到達するとき、光1はC’に存在することがわかります。
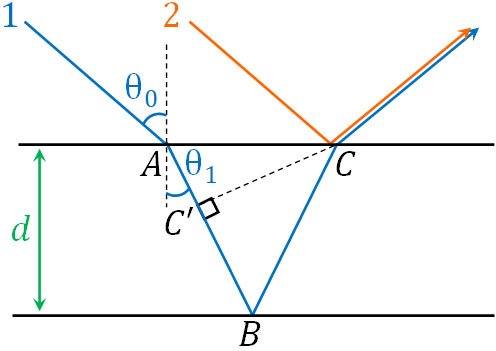
そのため光1と光2の距離の差は以下になるとわかります。
- \(C’B+BC\)
こうして、計算するべき距離がわかりました。そこでBCについて、下図のように線対象となる線を作りましょう。
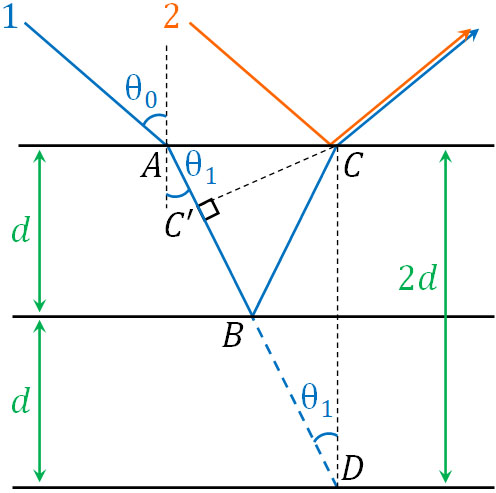
つまり、経路差はC’Dとなります。図より、C’Dは以下のように計算できます。
- \(C’D=2dcosθ_1\)
ただ\(2dcosθ_1\)は経路差であり、私たちは光路差を計算しなければいけません。空気中と薄膜では、光の速さが異なります。速さが異なる場合、波の干渉に関する計算が難しいです。そこで薄膜中を進む光について、空気中(真空中)を進んだと仮定して距離を出すのです。
2つの光が強め合うかどうかというのは、同じ条件下での距離の差を計算しなければいけません。そこで薄膜中を進む光について、屈折率\(n\)をかけることで光学距離を出しましょう。つまり、2つの光の光路差は\(2ndcosθ_1\)になります。
光の反射により、位相が変化する:薄膜での干渉条件の公式
こうして、光1と光2の光路差を得ることができました。ただ屈折率の異なる媒質で反射する場合、自由端反射になることがあれば、固定端反射になることもあります。
光2では、空気(屈折率が小さい)から薄膜(屈折率が大きい)へ進む過程で光の反射が起こっています。薄膜は屈折率が大きく、固定された壁となるため固定端反射が起こり、光2は逆位相になります。
一方で光1では、薄膜から空気へ進む過程で光の反射が起こっています。そのため自由端反射となり、位相の逆転は起こりません。つまり、光1と光2は逆位相となっています。
位相が逆となっている波が強め合うためには、半波長の奇数倍であればいいです。そのため、薄膜での明線条件は以下になります。
- \(2ndcosθ_1=\displaystyle\frac{λ}{2}×(2m+1)\) (\(m=0,1,2…\))
一方で2つの波が弱め合うためには、半波長の偶数倍であればいいです。そのため、薄膜での暗線条件は以下になります。
- \(2ndcosθ_1=\displaystyle\frac{λ}{2}×2m\) (\(m=0,1,2…\))
波の干渉条件を学ぶとき、公式を覚えても意味がありません。応用問題が出されると公式を利用できないからです。そこで、薄膜で波の干渉が起こるときの原理を理解しましょう。
白色光が薄膜に当たると虹色に見える
前述の通り、シャボン玉や水に浮かんでいる油など、薄膜に白色光が当たると虹色に見えます。ここまで学んだことを利用すれば、なぜシャボン玉が虹色に見えるのかわかります。
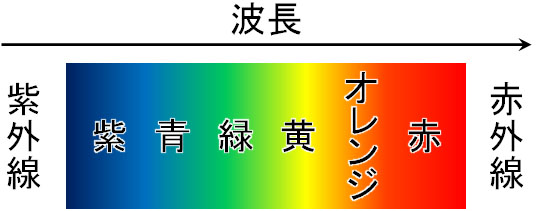
太陽光など、白色光はさまざまな可視光を含んでいます。また色によって波長が異なります。
 先ほど計算した通り、光が強め合う、または弱め合うときは以下のときになります。
先ほど計算した通り、光が強め合う、または弱め合うときは以下のときになります。
- \(2ndcosθ_1=\displaystyle\frac{λ}{2}×(2m+1)\) (\(m=0,1,2…\))
- \(2ndcosθ_1=\displaystyle\frac{λ}{2}×2m\) (\(m=0,1,2…\))
つまり波長が違えば、光が屈折するときの角度θが異なります。色によって屈折する角度が異なるというのは、青色や黄色、赤色などの色が異なる場所に表れることを意味しています。そのため、薄膜に白色光が当たると虹色に見えるのです。
薄膜の干渉に関する練習問題
それでは、波の干渉に関する薄膜での練習問題を解きましょう。以下の問題の答えは何でしょうか。
- ガラスの表面を厚さ\(d\)、屈折率\(n\)の薄膜でコーティングしました。下図のように入射角を\(θ_0\)、屈折角を\(θ_1\)とするとき、光の干渉によって薄膜は色づいています。なお、ガラスの屈折率は\(n\)よりも大きいです。
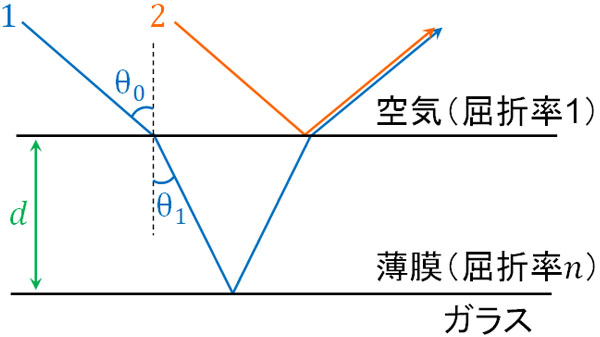
- 光が干渉によって強め合う条件を記しましょう。
- 単色光が\(θ_0=0\)で入射するとき、干渉によって光が弱め合うときの最小の膜の厚さはいくらでしょうか。
1) 光が干渉によって強め合う条件を記しましょう
2つの光の光路差は既に説明した通り\(2ndcosθ_1\) です。そのため、\(2ndcosθ_1\) を得る過程の説明は省略します。
空気中(真空中)は屈折率が1であり、薄膜の屈折率は\(n\)です。屈折率1は最も小さい値なので、\(n>1\)です。そのため、薄膜の表面で反射する光は固定端反射によって逆位相になります。
また問題文より、薄膜の屈折率\(n\)よりも、ガラスの屈折率のほうが大きいです。つまり薄膜よりも、ガラスのほうが光の進む速度は遅く、光が反射するときは固定端反射します。そのため、光1と光2は両方とも固定端反射によって位相が逆になり、結果として同位相になります。
同位相の波が強め合うためには、半波長の偶数倍になればいいです。そのため光が干渉することによって強め合うためには、以下の条件を満たせばいいです。
- \(2ndcosθ_1=\displaystyle\frac{λ}{2}×2m\) (\(m=0,1,2…\))
こうして、式を得ることができました。公式を暗記しても答えを得ることはできませんが、薄膜で発生する波の干渉の原理を学んでいれば容易に答えを得ることができます。
2) 単色光が\(θ_0=0\)で入射するとき、干渉によって光が弱め合うときの最小の膜の厚さはいくらでしょうか。
入射角が0であるため、真上から光を当てることになります。また波の干渉によって弱め合うことになるため、先ほどとは異なり、干渉条件は半波長の奇数倍になります。
- \(2ndcosθ_1=\displaystyle\frac{λ}{2}×(2m+1)\) (\(m=0,1,2…\))
そこで、式に\(θ_1=0\)を代入しましょう。
\(2ndcos0°=\displaystyle\frac{λ}{2}×(2m+1)\)
\(4nd=λ(2m+1)\)
\(d=\displaystyle\frac{λ(2m+1)}{4n}\)
なお、\(d\)の値は\(m\)の値によって変わります。光が弱め合うときの最小値を知りたいため、\(m=0\)を代入しましょう。これにより、\(d=\displaystyle\frac{λ}{4n}\) が答えであるとわかります。
薄膜での干渉条件を理解する
解き方を覚えていないと答えを得られないケースは多く、その一つが薄膜での干渉条件です。波の干渉条件を学ぶとき、公式を暗記するのではなく、必ず公式の導き出し方を理解しましょう。
薄膜の干渉条件では、ここまで説明した通り、距離の差(経路差)ではなく、光路差を用いて干渉条件を計算する必要があります。また媒質の屈折率によって自由端反射になるのか、それとも固定端反射になるのかが異なります。
そこで問題文から、光路差と反射の種類(自由端反射または固定端反射)を確認しましょう。公式を覚えても問題を解けないのは、問題文によって得られる答えが変わるからです。
物理では自然現象が起こる原理を学ばなければいけません。そこで、薄膜でどのように光が干渉するのか理解しましょう。






