電気を学ぶとき、重要な内容にコンデンサーがあります。回路にコンデンサーが含まれていることは多く、公式を利用することで問題を解きましょう。
ただ、公式を覚えても応用問題を解けません。そこで、コンデンサーの仕組みを理解しましょう。また、なぜ公式が成り立つのかを学び、公式を導出できるようになりましょう。
電荷が移動し、電荷を蓄えることのできる装置がコンデンサーです。また電荷を蓄積した後、放電することもできます。放電によって電気を流すことにより、一瞬だけ機器類を動かすことが可能なのです。そのため、コンデンサーは多くの電子機器の部品としてひんぱんに利用されています。
それでは、コンデンサーの仕組みはどうなっているのでしょうか。また、利用する公式には何があるのでしょうか。電磁気学で必ず学ぶコンデンサーについて解説していきます。
もくじ
電荷を蓄積できる装置がコンデンサー:極板への充電の仕組み
コンデンサーを利用する場合、電流が流れることで、コンデンサーに電荷が蓄積します。コンデンサーの構造はシンプルであり、二枚の金属板を向かい合わせに設置します。なお、コンデンサーでは金属板を極板といいます。

上図について、スイッチを入れて電流を流すとコンデンサーはどのような状態になるでしょうか。電極とコンデンサーをつなぐことにより、電子が移動します。言い換えると、電流\(I\)が流れます。電流は正極から負極に流れる一方、自由電子は電流とは反対向きに流れます。
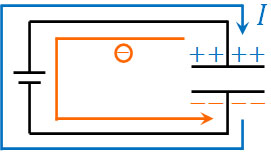
自由電子が負極側へ流れることにより、負極側は負に帯電します。また正極側では、電子が少なくなるので正に帯電します。こうして、極板には電位差が生まれます。電位差がある場合、電場が生まれます。
充電によって電位差が電源と等しくなると、電流は流れなくなる
時間経過と共に、電源による影響によって電子が移動し、極板に蓄積する電気量は増加します。つまり、電位差が大きくなります。ただ電位差が継続して大きくなることはなく、極板の電位差が電源の電位差と等しくなると、電流は流れなくなります。
電圧というのは、電気的な高さを表します。そのため、オリジナルの高さ(電源の電圧)よりも高い状態にすることはできません。コンデンサーの電圧(電位差)というのは、最も高くても電源の起電力となるのです。
また電源の起電力(電位差)とコンデンサーの電位差が等しい場合、電流が流れないことは問題なく理解できると思います。
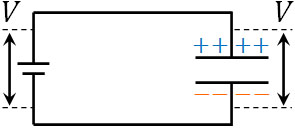
高さが同じ場合、水は流れません。同じように、電気的な高さが同じ場合、電流は流れないのです。
なお、コンデンサーに電荷を蓄積する操作を充電といいます。充電によって電気量を蓄え、電源と同じ電位差になれるのがコンデンサーです。
・極板の電気量は必ず同じになる
コンデンサーでは、一方の電荷がもう一方へ移動することになります。そのため、正極板と負極板に蓄積する電気量の絶対値は必ず等しくなります。例えば正極板の電気量が+10Cの場合、負極板の電気量は必ず-10Cになります。
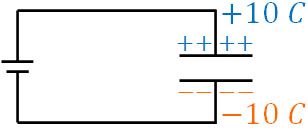
なお充電した後、スイッチを切ると電源とコンデンサーは完全に切り離されることになります。この場合であっても、コンデンサーには電荷が蓄えられたままとなります。
電荷の偏りがある場合、静電気力によって引き付けあう力が働きます。極板にある正電荷と負電荷は静電気力(クーロン力)によって引き合うため、スイッチを切ったとしても電荷はコンデンサーに蓄積したままとなるのです。
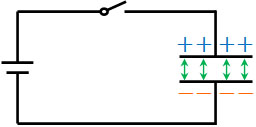
充電によってコンデンサーに電荷を蓄積させるとき、コンデンサーにはこうした性質があることを学びましょう。
放電により、コンデンサーの電荷が流れる
なお充電が可能であるため、コンデンサーは放電することもできます。蓄えた電荷を電流として流す操作を放電といいます。
例えば、コンデンサーを充電させた後、電源を電球に変えてスイッチを入れましょう。この場合、コンデンサーに蓄積していた電荷が移動します。つまり、充電時とは逆向きに電流と電子が流れます。
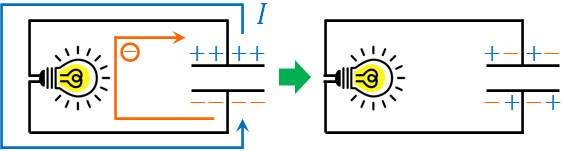
放電した後では、コンデンサーの電位差はゼロになります。極板に電荷がない状態へ戻ることにより、中性の状態となるのです。コンデンサーによる放電は一瞬で起こります。
なおコンデンサーによる放電が行われ、中性の状態になると、再び充電が可能になります。電源に接続することにより、コンデンサーに対して電荷を蓄えさせることができるのです。
コンデンサーで利用する3つの公式
それでは、コンデンサーで利用される公式には何があるのでしょうか。まず、極板の面積が\(S\)、極板間の距離が\(d\)、誘電率\(ε\)のコンデンサーがあるとします。
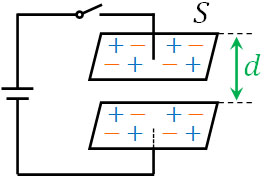
電気量が\(Q\)、電圧が\(V\)、電気容量が\(C\)、電場が\(E\)の場合、以下の3つの公式がコンデンサーで重要です。
- \(Q=CV\)
- \(V=Ed\)
- \(C=ε\displaystyle\frac{S}{d}\)
これらの公式が何を意味しているのか理解しましょう。
なお\(V=Ed\)は既に理解していると思います。電場\(E\)は傾きであり、電圧\(V\)と距離\(d\)によって得ることができます。
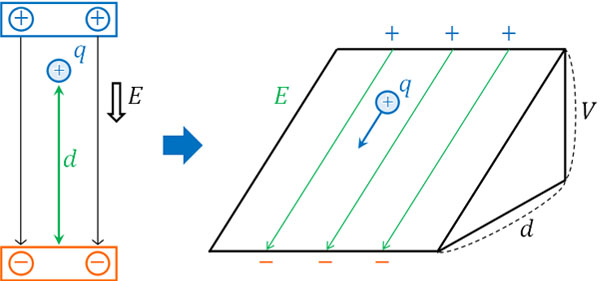
それに対して、\(Q=CV\)と\(C=ε\displaystyle\frac{S}{d}\)はコンデンサーで学ぶことになる公式です。そこで、この2つの公式が何を意味しているのか理解しましょう。
コンデンサーの電気量\(Q\)と電圧\(V\)、電気容量\(C\)の関係
コンデンサーに関する公式で基本となる公式が\(Q=CV\)です。\(C\)は比例定数であり、電気容量といいます。電気容量の単位はF(ファラド)であり、C/Vも電気容量の単位です。
電気容量\(C\)とは、どれだけコンデンサーに電気を蓄積できるのかを表す比例定数です。同じ電圧であっても、電気容量の大きいコンデンサーであるほど、電気の蓄積量(電気量\(Q\))が大きくなります。
なお重要なのは、\(Q=CV\)を見てわかる通り、「電気量\(Q\)は電圧\(V\)に比例する」という事実です。電圧\(V\)が大きい場合、それに比例して電気量\(Q\)も大きくなります。
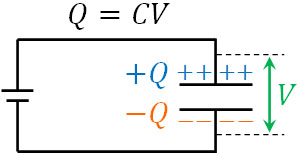
なお電圧\(V\)というのは、電源の起電力ではありません。コンデンサーの電位差がコンデンサーの公式で利用される電圧\(V\)です。電源の起電力(電位差)ではなく、コンデンサーの電位差を利用して計算しましょう。
ガウスの法則を利用し、極板間の電場と電気量を計算する
それでは、ガウスの法則を利用することによってコンデンサーの公式を導出しましょう。面積\(S\)の金属板が電気量\(Q\)で一様に帯電しており、クーロン定数を\(k\)とします。そうすると、ガウスの法則より、電気力線の本数は\(4πkQ\)となります。
※ガウスの法則を既に理解している前提で話を進めていきます。
なお電気力線の定義より、電場の大きさが\(E\)の場合、1m2に\(E\)[本]の電気力線を書くことができます。また金属板の面積は\(S\)[m2]であり、上側と下側から電気力線が出ているため、両方の面積を足すと\(2S\)です。
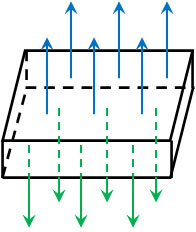
そのため、以下の計算によって金属板から発せられる電場\(E\)がわかります。
\(E=\displaystyle\frac{4πkQ}{2S}=\displaystyle\frac{2πkQ}{S}\)
なおコンデンサーでは、2枚の金属板が存在します。正極板では、電場が発生しています。一方で負極板では、正極板とは反対向きの電場となります。
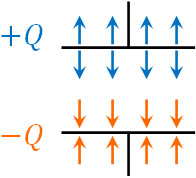
そこで、正極板と負極板の電場を足しましょう。図にすると、以下のようになります。
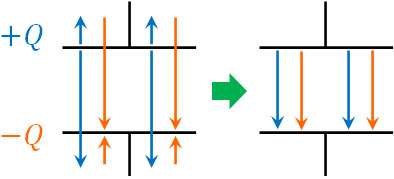
コンデンサーの外側では、反対向きの電場によって打ち消し合い、電場はゼロになります。一方でコンデンサーの内側では、2つの電場が重なります。
先ほど計算した通り、一枚の金属板から放出される電場は\(E=\displaystyle\frac{2πkQ}{S}\)です。コンデンサーには二枚の金属板があるため、2倍しましょう。つまりコンデンサーの内側では、電場は\(E=\displaystyle\frac{4πkQ}{S}\)となります。
なお\(V=Ed\)であり、\(E=\displaystyle\frac{4πkQ}{S}\)を代入しましょう。そうすると、以下の式を作ることができます。
\(V=Ed\)
\(V=\displaystyle\frac{4πkQ}{S}d\)
\(Q=\displaystyle\frac{S}{4πkd}V\)
ここで、\(C=\displaystyle\frac{S}{4πkd}\)とすると、\(Q=CV\)になるとわかります。
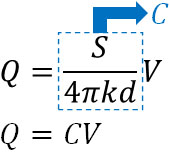
こうして、ガウスの法則と電場の関係を利用することによって、コンデンサーで利用される公式を導き出すことができました。
面積と距離で変化するコンデンサーの電気容量\(C\)
次に、コンデンサーの電気容量\(C\)が何を意味しているのか確認しましょう。先ほどの式を見てわかる通り、電気容量\(C\)は以下の式によって表すことができます。
- \(C=\displaystyle\frac{S}{4πkd}\)
このとき、円周率\(π\)とクーロン定数\(k\)は定数であり、値に変化はありません。そこで、\(\displaystyle\frac{1}{4πk}\)を誘電率\(ε\)(イプシロン)としましょう。\(ε=\displaystyle\frac{1}{4πk}\)であるため、以下の式に変形できます。
- \(C=ε\displaystyle\frac{S}{d}\)
こうして、電気容量\(C\)を得る公式を導き出すことができました。
式を見てわかる通り、電気容量\(C\)は金属板の面積\(S\)が大きいほど、値は大きくなります。面積が大きければ、より多くの電荷を蓄積できるのは容易に想像できます。
また電気容量\(C\)は極板間の距離が小さいほど大きくなるとわかります。この理由としては何があるのでしょうか。
極板に電荷がある場合、静電気力(クーロン力)によって引き合います。当然ながら、静電気力は距離が近いほど影響が強いです。つまり、2つの金属板の距離が近いほど、正電荷と負電荷による引き合いの力が強くなり、コンデンサーに電荷が蓄積します。
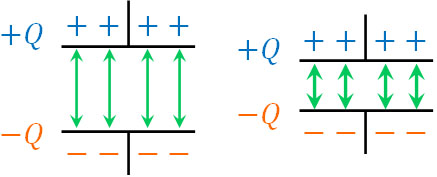
こうした理由があるため、極板間の距離が小さいほど電気容量\(C\)は大きくなるのです。
電気容量\(C\)がなぜ面積\(S\)に比例し、極板間の距離\(d\)に反比例するのか理解すれば、電気容量\(C\)の公式の意味がわかります。
公式を利用し、コンデンサーに関する練習問題を解く
それでは、ここまで学んできたことを利用してコンデンサーに関する問題を解いてみましょう。以下の問題の答えは何でしょうか。
- コンデンサーに電気量\(Q\)が蓄積しており、電気容量は\(C\)です。極板間の距離が\(d\)のとき、電場の大きさ\(E\)を求めましょう。
\(Q=CV\)なので、\(V=\displaystyle\frac{Q}{C}\)です。また\(V=Ed\)であり、\(V=\displaystyle\frac{Q}{C}\)を代入しましょう。
\(V=Ed\)
\(\displaystyle\frac{Q}{C}=Ed\)
\(E=\displaystyle\frac{Q}{Cd}\)
こうして、電場の大きさは\(E=\displaystyle\frac{Q}{Cd}\)とわかりました。次に、以下の問題を解いてみましょう。
- コンデンサーに電気量\(Q\)が蓄積しており、電位差は\(V\)、極板の面積は\(S\)、誘電率は\(ε\)です。コンデンサーの極板間の距離\(d\)を求めましょう。
\(Q=CV\)であり、\(C=ε\displaystyle\frac{S}{d}\)です。そのため、以下のように計算できます。
\(Q=CV\)
\(Q=ε\displaystyle\frac{S}{d}×V\)
\(d=\displaystyle\frac{εSV}{Q}\)
こうして、極板間の距離は\(d=\displaystyle\frac{εSV}{Q}\)と計算できます。
コンデンサーの仕組みと公式の意味を学ぶ
電気回路にとってコンデンサーは重要です。コンデンサーによって電気の蓄積(充電)や放電が可能になります。
そこで、コンデンサーの仕組みを理解しましょう。電源の起電力により、自由電子が移動します。電流が流れることによって、コンデンサーに電荷が蓄積するのです。その後、放電によってコンデンサーの電荷はゼロになります。
コンデンサーで利用される重要な公式は3つです。なぜ、これらの公式が成り立つのか学びましょう。ガウスの法則を利用して、公式の導出を行えるようになる必要があります。そうすれば、公式の意味が分かります。
コンデンサーを理解できない人は多くの場合、回路で何が起こっているのか理解しておらず、公式を暗記しているだけです。それでは意味がないため、必ずコンデンサーの仕組みを学び、公式を導き出せるようになりましょう。






