私たちが毎日の生活で利用している電気は交流電流です。時間によってプラスとマイナスが周期的に変化するのが交流です。
電気を学ぶとき、交流よりも先に直流を学びます。直流のほうが直感的に理解しやすいからです。一方で交流の場合、時間によって電圧が変化します。そのためグラフは複雑になり、角度を利用することで電圧を計算しなければいけません。
それでは発電するとき、なぜ直流ではなく交流となるのでしょうか。また、交流電源を利用するときの公式やグラフはどのようになるのでしょうか。
直流と交流では性質が大きく異なります。なぜ交流電流を生じるのか、またどのように交流の公式を利用すればいいのか解説していきます。
もくじ
直流電源と交流電源の違い
電源には主に二種類あり、直流電源と交流電源があります。私たちが電気を学ぶとき、交流電源よりも先に直流電源を学びます。直流電源では常に電圧\(V\)が同じです。そのためイメージしやすく、計算が容易です。

一方で交流電源では、時間経過と共に電圧が変化します。以下のように、電圧がプラスになることがあれば、マイナスになることもあります。
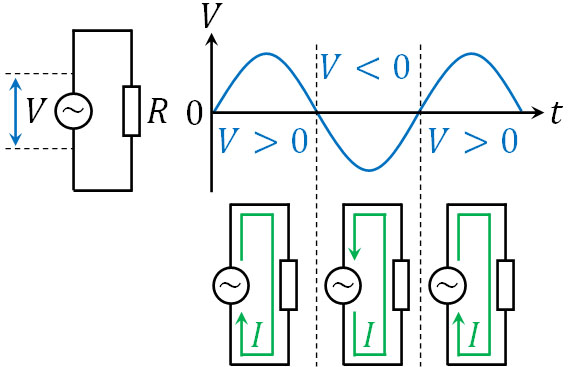
直流電源では、電流が一方通行となります。それに対して交流電源では、電圧がプラスになったりマイナスになったりするため、時間によって電流の向きが異なります。また、電流の大きさも変化します。直流電源と交流電源では、このように大きな違いがあるのです。
電磁誘導による発電なので、電気は交流となる
それでは、電池とは異なりなぜ私たちが利用する電流は交流なのでしょうか。この理由として、電磁誘導を利用して発電しているからです。
火力発電や風力発電など、発電するときは磁石とコイルで構成されている発電機を回転させる必要があります。磁場が存在する状況でコイルが回転する、またはコイルが存在する状況で磁石が回転すると、コイル周辺の磁場が変化します。
コイルは磁場の変化を嫌うため、磁場の変化を弱めるように電流と磁場を発生させます。こうして電磁誘導が起き、電気を得ることができるのです。
なお一様な磁場が存在するとき、コイルを回転させると、コイルは磁場に対して垂直になることがあれば、平行になることもあります。

磁場とコイルが平行なとき、電磁誘導は起こりません。一方でコイルが磁場を垂直に横切る場合、強い電磁誘導が起こります。
またコイルが回転するとき、一つの辺に着目すると、N極側を横切ることがあれば、S極側を横切ることもあります。N極とS極では磁場の性質が逆であるため、電磁誘導によって発生する電流と起電力の向きも逆になります。そのため、発電所で作られる電流は交流なのです。
交流電源での電圧の式とグラフ
それでは、交流電源ではどのような公式を利用すればいいのでしょうか。先ほど、交流電源での電圧のグラフを記しました。グラフをみてわかる通り、円運動や波と同じ形をしています。つまり、角度(sinθやcosθ)を利用すればいいとわかります。
角度が0°のとき、\(sin0°=0\)であり、\(cos0°=1\)です。そのため、出発地点によってsinθとcosθを使い分けましょう。具体的には、以下のようになります。
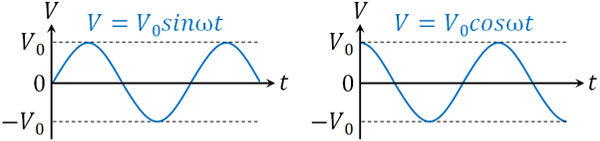
力学で等速円運動を学んでいる場合、この公式を問題なく理解できると思います(力学や波を理解していない場合、必ずこれらの分野を復習しましょう)。
最大電圧(最小電圧)が\(V_0\)であれば、sinθまたはcosθに\(V_0\)をかける必要があります。また時間経過によって角度が変わるため、角度θを\(ωt\)によって表します。\(ωt\)を位相といいます。こうして、電圧の式を得ることができます。
\(-1≦sinωt≦1\)であり、\(-1≦cosωt≦1\)です。そのため、\(V_0sinωt\)と\(V_0cosωt\)というのは、\(-V_0\)から\(V_0\)の範囲で電圧が規則正しく変化することを意味しています。そこで、\(t=0\)のときの電圧を確認し、\(sinωt\)または\(cosωt\)を利用しましょう。
なお位相によって電圧が変化するため、当然ながら電流も周期的に変化します。電流の式についても、\(I=I_0sinωt\)または\(I=I_0cosωt\)となります。
周期と周波数、角周波数の関係
なお交流では円運動を利用することになるため、周期\(T\)と周波数\(f\)の関係を理解しましょう。波動を学ぶとき、周期\(T\)と周波数\(f\)がひんぱんに出てくるため、波を学んでいる人は既に理解していると思います。
一周して元の場所に戻るまでの時間が周期\(T\)です。言い換えると、1回の振動をするために必要な時間が周期\(T\)です。また1秒間に何回の振動をするのかを表すのが周波数\(f\)です。周期\(T\)と周波数\(f\)には以下の関係があります。
- \(T=\displaystyle\frac{1}{f}\)
また、交流で重要な関係に角周波数\(ω\)と周期\(T\)があります。力学では、\(ω\)を角速度といいます。一方で交流では\(ω\)を角周波数といいます。名前は異なるものの、同じものと理解しましょう。
角周波数(角速度)は弧度法で表すため、30°や90°ではなく、\(\displaystyle\frac{π}{6}\)や\(\displaystyle\frac{π}{2}\)によって角度を表します。また、一秒間で進む角度が角周波数\(ω\)です。
前述の通り、一周するために必要な時間が周期\(T\)です。そのため角周波数\(ω\)と周期\(T\)をかけると、\(2π\)(360°)になるとわかります。そのため、以下の関係が成り立ちます。
- \(ωT=2π\)
等速円運動や波動を学ぶとき、\(ωT=2π\)の式は何度も利用します。交流であっても、\(ωT=2π\)を利用する場面は多いため、この式が何を意味しているのか復習しましょう。
交流電圧での実効値とは何か
力学や波動を学んでいる場合、ここまでの内容はそこまで難しくはありません。グラフの形や公式は等速円運動や波動と完全に同じだからです。
ただ、交流に特徴的な内容もあります。その一つが実効値です。例えば家庭で利用される電圧が100Vとしましょう。国によって規定されている電圧は異なるものの、ひとまず標準電圧が100Vの国にあなたが住んでいると仮定します。
ここまでの内容を理解すれば、電圧が100Vというのは明らかに変であるとわかります。交流電源なのであれば、時間経過と共に電圧が常に変化するからです。直流電源とは異なり、交流電源では常に電圧が100Vであることはありません。
ただ「電圧は\(100sinωt\)[V]」などと正確に表記されると、ほとんどの人は理解できません。そこで、本来は電圧が変化するものの、直流電源のように標準的な電圧を設定しましょう。この電圧が実効値です。私たちが日常生活で目にする電圧は実効値なのです。
「実効値に対して、\(\sqrt{2}\)倍すると最大電圧になる」というルールがあります。例えば100Vの交流電源であれば、最高電圧は約141Vです(\(\sqrt{2}≒1.41\))。
- \(100\sqrt{2}≒141\)
実効値よりも、最大電圧のほうが値は大きくなります。また、同じことは電流にもいえます。電流の実効値を\(\sqrt{2}\)倍すると、最大電流になります。そこで電圧と電流の実効値をそれぞれ\(V_e\)、\(I_e\)、最大電圧と最大電流を\(V_0\)、\(I_0\)とすると、以下の関係が成り立ちます。
- \(V_0=\sqrt{2}V_e\)
- \(I_0=\sqrt{2}I_e\)
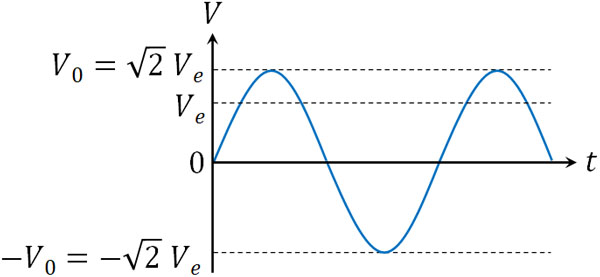
実効値を\(\sqrt{2}\)倍すると、最大値になることを理解すれば、この公式が何を意味しているのか分かります。
なぜ実効値では\(\sqrt{2}\)を利用するのか
それでは、なぜ実効値では\(\sqrt{2}\)を利用するのでしょうか。2倍ではダメなのでしょうか。もちろん、実効値で\(\sqrt{2}\)を利用するのは理由があります。そこで、以下のような単純な交流回路を考えましょう。

私たちが家電製品を利用するとき、電力\(P\)を基準に考えることが多いです。電力の単位はW(ワット)であり、W(ワット)を利用してどれだけの電力を消費したのかを表すことができます。なお、電力\(P\)を得る公式は以下になります。
- \(P=IV\)
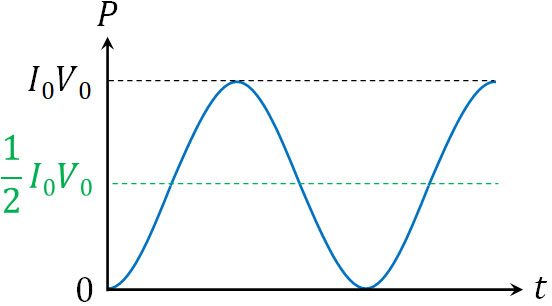
交流では前述の通り、電圧と電流が変化します。また電圧が強い場合、先ほどの回路であれば、電流も強くなります。最大電圧を得るとき、電流も最大になるのです。そこで電力\(P\)(電流\(I\)×電圧\(V\))のグラフを描くと以下のようになります。

電圧がマイナスのとき、電流もマイナスとなるため、かけ算をすると正の値になります。そのため、電力は常に正の値となります。
グラフを見てわかる通り、交流では電力が0となる場所があれば、最大値となる場所もあります。ただ、これではわかりにくいため、電力の平均値\(\overline{P}\)を計算しましょう。円運動では、山と谷の面積は同じです。そのため、最大値の半分が平均値になります。
- \(\overline{P}=\displaystyle\frac{1}{2}I_0V_0\)
なお抵抗での消費電力(家電製品の消費電力)について、電圧と電流でそれぞれ\(\displaystyle\frac{1}{2}\)を分担すると以下のようになります。
- \(\overline{P}=\displaystyle\frac{1}{\sqrt{2}}I_0×\displaystyle\frac{1}{\sqrt{2}}V_0\)
この式より、\(I_e=\displaystyle\frac{1}{\sqrt{2}}I_0\)であり、\(V_e=\displaystyle\frac{1}{\sqrt{2}}V_0\)です。これが、\(\sqrt{2}\)を利用する理由です。また、先ほどの式は以下のようになります。
- \(\overline{P}=I_eV_e\)
こうして、電圧と電流の実効値を利用することにより、消費電力の平均を得ることができます。実効値というのは、電力が平均となるときの電流や電圧の値を指すのです。言い換えると、交流を直流に換算するとき、どれくらいの値になるのかの指標が実効値です。
例えば同じ抵抗を利用する場合、直流電源で電圧が100Vなのと、交流電源で実効値が100Vのケースを比べると、流れる電流は同じです。交流での実効値というのは、直流に変換するときの電圧と電流を表します。
交流の概念を学び、実効値の意味を知る
直流電源と交流電源は大きく性質が異なります。ただ私たちが日常的に利用している電流は交流であり、直流ではありません。これは、電磁誘導によって生み出される電流が交流だからです。そこで、交流の概念を学びましょう。
直流とは異なり、交流では常に電圧が変化しています。ただ、最大電圧と最小電圧は一定であり、特定の周期で繰り返されます。そのためグラフの形は等速円運動や波動と同じであり、新たな概念ではありません。また、電圧を得る公式も円運動と同じです。
なお、交流で学ぶ新たな内容に実効値があります。交流電圧を直流電圧に換算するとき、いくらの電圧になるのかを表すのが実効値です。電力を利用して実効値を計算できます。また、実効値に\(\sqrt{2}\)をかけると最大電圧を得ることができます。
等速円運動と波動を学んでいる場合、交流電源で電圧を計算する公式を理解するのは簡単です。それに加えて、実効値が何を意味しているのか学びましょう。