単位面積に対してかかる力を圧力といいます。大気圧や水圧など、私たちは多くの場面で「圧力」という言葉を利用します。物理では圧力を計算することになり、さらには水圧を理解しなければいけません。
また圧力と親せき関係にあるのが浮力です。液体をどれだけ押しのけたのかによって浮力が決まります。水圧(圧力)の計算により、浮力の概念がわかります。
圧力や水圧、浮力については、公式を覚えなくても計算できます。公式を覚えるのではなく、圧力の定義を覚えましょう。また、なぜ浮力を生じるのか学びましょう。そうすれば、公式を覚えなくても答えを導き出すことができます。
それでは、どのように圧力や浮力の計算をすればいいのでしょうか。高校物理で重要な圧力と浮力を解説していきます。
もくじ
単位面積当たりにかかる力が圧力
圧力とは、単位面積当たりにかかる力を指します。そのため同じ大きさの力であっても、力の加わる面積が小さい場合、圧力は大きくなります。
例えば1kgの力であなたを押すとき、先のとがった鉛筆ととがっていないクレヨンでは、どちらのほうが痛いでしょうか。

当然、先のとがった鉛筆を利用するほうがあなたは強い痛みを感じます。言い換えると、先のとがった鉛筆では圧力が強いことを意味します。同じ力で押すにしても、触れている面積が狭いため、強い圧力がかかるのです。
つまり圧力\(P\)で重要なのは、力の大きさ\(F\)と面積\(S\)であるとわかります。圧力\(P\)は以下の公式によって得られます。
- \(P=\displaystyle\frac{F}{S}\)
ただ、この公式を覚える必要はありません。なぜなら、当たり前だからです。加える力の大きさ\(F\)が大きくなれば、圧力は大きくなります。
しかし、面積\(S\)が大きくなれば、その分だけあなたが感じる圧力は小さくなります。そこで圧力を計算するとき、力の大きさ\(F\)を面積\(S\)で割りましょう。圧力の定義を理解すれば、公式を覚えなくても公式を導き出すことができます。
パスカル(Pa)と大気圧
なお、圧力の単位はパスカル(Pa)です。1m2当たりに生じる力がパスカルです。力の単位はN(ニュートン)であるため、1Paは1N/m2と表すこともできます。
パスカルを最も利用する場面は大気圧です。天気予想で利用される単位はhPa(ヘクトパスカル)であり、1hPaは100Paを表します。また、大気圧(1気圧)は約1013hPaです。
空気中に存在する分子が衝突することによって大気圧を生じます。大気圧というのは、酸素分子や窒素分子が存在するために発生するのです。高い山に登ると大気圧が低くなるのは、その分だけ酸素分子や窒素分子の数が少なくなるからです。
水の重さによって水圧が生まれる
空気による圧力が大気圧なのに対して、水の重さによって生じる圧力が水圧です。それでは、水圧はどのように計算すればいいのでしょうか。浮力を理解するときに重要な概念が水圧であるため、水圧の計算方法を理解しましょう。
水深が深くなれば、水圧が大きくなることは物理を学んでいなくても既に知っていると思います。水深1mと水深100mでは、当然ながら水深100mのほうが水による圧力が大きくなります。
水圧というのは、特定の位置よりも上にどれだけの水が存在するのかによって決まります。水深が深くなるほど、物体の上には多くの水が乗っかってくるからです。
そのため水面から特定の深さについて、面積\(S\)m2に存在する水の重さを\(m\) kgとすると、重力加速度は\(g\)なので、水による力(重力)は\(mg\)です。また面積は\(S\)m2なので、水圧\(P\)は以下のように計算できます。
\(P=\displaystyle\frac{mg}{S}\)
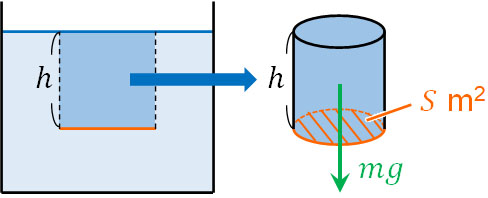
要は、水の重さに重力加速度をかけ、面積で割れば水圧を得ることができます。
なお、水の質量は水の密度\(ρ\)kg/m3と体積をかけることで得ることができます。水の体積は底面積\(S\)と高さ(水深)\(h\)をかけることで得られます。つまり、水の質量\(m\)は\(ρSh\)と変換できます。
そこで、先ほどの式へ\(m=ρSh\)を代入しましょう。
\(P=\displaystyle\frac{mg}{S}\)
\(P=\displaystyle\frac{ρSh×g}{S}\)
\(P=ρhg\)
こうして、水圧は水の密度\(ρ\)kg/m3、高さ(水深)\(h\)、重力加速度\(g\)をかけることによって得られるとわかります。1m3あたりの質量が密度であるため、密度の定義を理解すれば、圧力の公式から水圧を得る公式を容易に導き出すことができます。
なお海やプールなど、水の環境によって密度は異なるものの、あなたが水に潜るときは常に同じ環境による水の影響を受けます。つまり潜る場所が同じなのであれば水の密度\(ρ\)kg/m3は一定です。また重力加速度\(g\)も一定です。つまり、水圧は水深\(h\)のみに依存することがわかります。
・大気圧を考慮する場合の水圧
水のみを考慮する場合、水圧は\(ρhg\)によって計算できます。ただ実際には、水の上には大気が存在します。そのためすべての圧力を計算するとき、水圧\(ρhg\)に大気圧\(P_0\)を足します。つまり、すべての圧力は以下のようになります。
- \(P=P_0+ρhg\)
水圧を利用し、浮力を計算する
水圧を学べば、浮力を理解できます。水圧は横からだけでなく、すべての方向で水圧が生まれます。つまり、物体はあらゆる方向から水によって押されることになります。
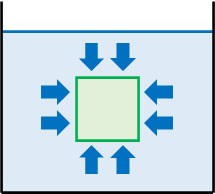
重要なのは、物体の上面と下面で水圧が異なる事実です。前述の通り、水圧は水深に比例します。つまり上面に加わる水圧と下面に加わる水圧を比べると、下面に加わる水圧のほうが大きいです。そのため物体が水の中に入ると、下面からの水圧によって押し上げられます。これが浮力です。
それでは、浮力を計算してみましょう。上面の水深を\(h_1\)、下面の水深を\(h_2\)とします。この場合、上面にかかる水圧\(P_1\)は\(ρh_1g\)です。また底面積が\(S\)の場合、上面にかかる力は\(ρh_1Sg\)になります。圧力は単位面積当たりに働く力なので、面積をかけることで全体の力を計算できます。
同様に、下面にかかる水圧\(P_2\)は\(ρh_2g\)です。また、下面にかかる力は\(ρh_2Sg\)になります。
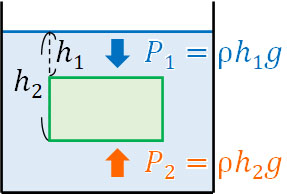
浮力は単位面積に働く力ではなく、物体全体に働く力です。そこで、下面全体に働く力\(ρh_2Sg\)から上面全体に働く力\(ρh_1Sg\)を引きましょう。
\(ρh_2Sg-ρh_1Sg\)
\(=ρ(h_2-h_1)Sg\)
なお、\(h_2-h_1\)は物体の高さです。そのため\(h_2-h_1\)に\(S\)をかけると、物体の体積\(V\)になります。そこで、先ほどの式に\((h_2-h_1)S=V\)を代入しましょう。
\(ρ(h_2-h_1)Sg\)
\(=ρVg\)
こうして、浮力は水の密度\(ρ\)kg/m3、物体の体積\(V\)m3、重力加速度\(g\)をかけることによって得られるとわかります。液体の密度度\(ρ\)と重力加速度\(g\)は一定です。そのため、浮力は物体の体積に依存することがわかります。
浮力は水深に関係なく一定です。浮力で重要なのは物体の体積だけです。
浮力を学べばアルキメデスの原理がわかる
ここまでの内容を学べば、アルキメデスの原理がわかります。以下がアルキメデスの原理です。
- 物体が押しのけた液体の体積と重さで浮力が決まる。
満杯の水層に物体を入れると、物体の体積分だけ水が外に出されます。このとき、外にでた水の量(=物体の体積)によって浮力が決まるというわけです。

先ほど、\(ρVg\)によって浮力を計算できると解説しました。また、浮力は物体の体積に依存することも述べました。これはつまり、アルキメデスの原理を意味しています。
また液体の種類を変えると浮力は変化します。例えば、水よりも水銀のほうが重いです。これは、水銀の密度は水の密度よりも大きいからです。排除された液体の量(体積)は同じであっても、水よりも水銀のほうが重いため、水銀のほうが浮力は大きくなります。
圧力・水圧・浮力は互いに関係している
物理では覚えなければいけない公式が少ないです。これは、容易に公式を導き出すことができるため、覚える必要がないのです。また公式を覚えても利用できないケースは多く、それよりも物理現象がなぜ起こるのか理解しましょう。
物理現象の原理原則を理解するべき内容の一つが圧力・水圧・浮力です。これらはすべて関係性があります。
公式を覚えなくても、圧力の定義を学べば圧力の公式を得らます。また、圧力の公式を利用することで水圧の公式と浮力の公式を得られます。なぜ、これらの公式を得られるのか理解すれば、応用問題が出されても問題を解くことができます。
圧力の公式を利用して水圧と浮力を得る方法を学び、自然現象がどのような原理で起こっているのか理解しましょう。






