未知の回路について、電圧や電流の値を知りたいときは電流計や電圧計を利用します。ただ、電流計や電圧計を利用する場合、内部抵抗が存在するために正確な値を測定することができません。
そこで、より正確に未知抵抗の値を知る方法としてホイートストンブリッジ回路が知られています。既にわかっている抵抗を利用することにより、測定したい部分の抵抗の値を知ることができるのです。具体的には、検流計に電気が流れないとき(平衡状態)の結果を利用します。
ホイートストンブリッジでは公式を覚えても意味がありません。応用問題を解くためには、原理や計算方法を理解する必要があります。
それでは、どのように電圧や電流、合成抵抗を利用して計算すればいいのでしょうか。ホイートストンブリッジを利用して、未知の抵抗を計算する方法を解説していきます。
もくじ
ホイートストンブリッジの回路:未知抵抗の値を求める
まず、ホイートストンブリッジ回路がどのような形になっているのか知りましょう。既に値がわかっている抵抗2つ、可変抵抗(抵抗の値を変更できる抵抗)、未知の抵抗、検流計を利用するのがホイートストンブリッジです。
既知の抵抗が\(R_1\)と\(R_2\)、可変抵抗を\(R_3\)、未知の抵抗を\(R\)とすると、以下の図を作ることができます。
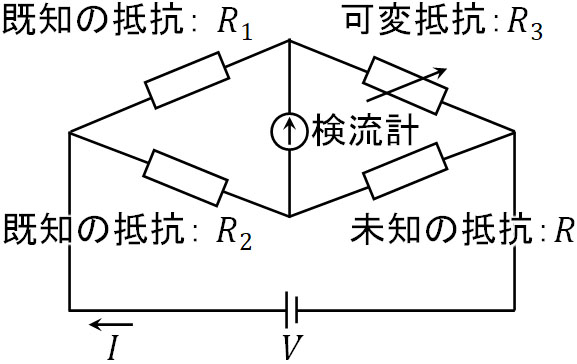
なお検流計とは、電流の強さと向きを調べられる装置を指します。図を確認すると、複雑に思えてしまいます。ただホイートストンブリッジでは、特殊なケースを利用して未知の抵抗を測定するため、条件を絞ることができます。
検流計に電気が流れないようにする:電流計・電圧計を使わない
それでは、特殊な条件とは何でしょうか。未知の抵抗を調べるとき、検流計に電気が流れていない状態(平衡状態)のときを条件として利用します。
可変抵抗を利用すれば、抵抗の値を変更できます。通常であれば、検流計に電流が流れます。ただ特定の条件では、検流計に電流が流れない状態があるため、この値を利用することによって未知の抵抗を計算できるのです。
未知の抵抗を調べるとき、電流計や電圧計を利用すればいいように思います。電圧と電流がわかれば、オームの法則によって抵抗を計算できます。ただ前述の通り、電流計や電圧計には内部抵抗があるため、正確な値を得ることはできません。
一方でホイートストンブリッジ回路であれば、検流計に電流が流れない状態を利用できます。検流計に電流が存在しないため、検流計による内部抵抗はありません。内部抵抗の影響がないため、ホイートストンブリッジ回路を利用する場合、電流計や電圧計を利用するときに比べて正確に測定できます。
平衡状態で回路を流れる電流
それでは、ホイートストンブリッジ回路を利用するとき、どのように計算すればいいのでしょうか。前述の通り、検流計に電流が流れていない平衡状態を利用します。
検流計に電流が存在しないため、検流計につながっている導線は無視できます。つまり、回路を以下のように考えることができます。
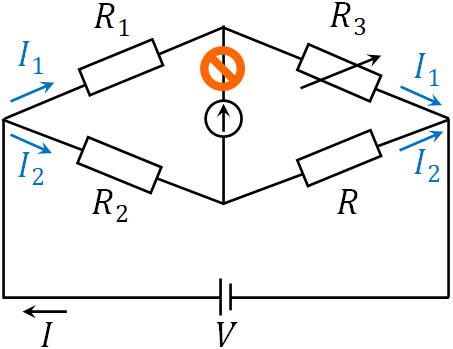
検流計につながっている導線では電流が存在しないため、既知抵抗\(R_1\)と可変抵抗\(R_3\)を流れる電流の大きさは同じです。また、既知抵抗\(R_2\)と未知抵抗\(R\)を流れる電流の大きさは同じです。
平衡状態では検流計に電流が存在しないため、回路の上側では電流の大きさが\(I_1\)となり、回路の下側では電流の大きさが\(I_2\)となります。
キルヒホッフの法則と等電位:公式は覚えてはいけない
次に、等電位であることを利用して式を作りましょう。電流が存在しないというのは、電位差(電圧)が存在しないことを意味します。つまり検流計の両側は等電位です。
検流計に電気が流れていないため、電流\(I\)の値は0です。そこで検流計の内部抵抗を\(r\)、電位差を\(V\)とすると、以下のように計算できます。
\(V=r×0=0\)
こうして、計算によっても検流計がつながっている導線は等電位になっており、電位差が存在しないとわかります。
そこで、キルヒホッフの法則を利用しましょう。キルヒホッフの第二法則では、回路を一周すると必ず電位差がゼロになります。また検流計に電気が流れておらず、電位差が存在しないため、検流計の影響を無視できます。そこで、以下の部分を利用して式を作りましょう。
\(R_1I_1-R_2I_2=0\)
\(R_1I_1=R_2I_2\)
\(\displaystyle\frac{R_1}{R_2}=\displaystyle\frac{I_2}{I_1}\)
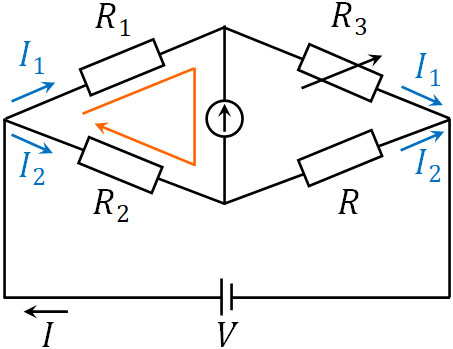
次に、以下の部分に着目して式を作りましょう。
\(R_3I_1-RI_2=0\)
\(R_3I_1=RI_2\)
\(\displaystyle\frac{R_3}{R}=\displaystyle\frac{I_2}{I_1}\)
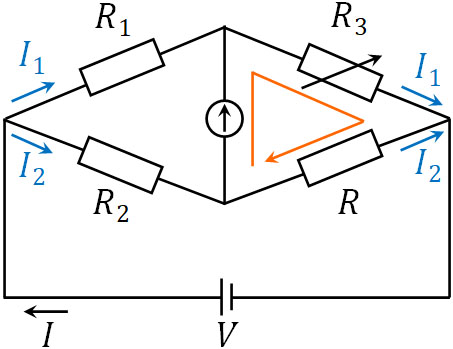
\(\displaystyle\frac{R_1}{R_2}=\displaystyle\frac{I_2}{I_1}\)と\(\displaystyle\frac{R_3}{R}=\displaystyle\frac{I_2}{I_1}\)より、以下の式を作れます。
\(\displaystyle\frac{R_1}{R_2}=\displaystyle\frac{R_3}{R}\)
\(R=\displaystyle\frac{R_2R_3}{R_1}\)
こうして、未知の抵抗は\(R=\displaystyle\frac{R_2R_3}{R_1}\)とわかります。検流計を利用して得られる値がゼロのとき(検流計に電流が存在しないとき)、\(R=\displaystyle\frac{R_2R_3}{R_1}\)によって未知抵抗を計算しましょう。
なお、この公式を覚えてはいけません。ホイートストンブリッジ回路を利用して、公式を作れるようにしましょう。
直列接続とみなし、合成抵抗を計算する
なおホイートストンブリッジ回路では、合成抵抗を計算しなければいけないケースもあります。検流計に電気が流れていない場合、合成抵抗の計算は簡単です。
検流計に電流が存在しないのであれば、検流計につながっている導線を無視できます。つまり、「検流計につながっている導線が存在しない」とみなすことができます。そうすると、以下の回路へ変換できます。
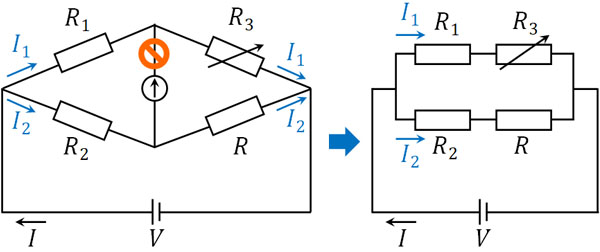
直列接続では、抵抗を足せばいいです。そのため、それぞれの合成抵抗は以下のようになります。
- \(R_1+R_3\)
- \(R_2+R\)
また並列接続の場合、逆数を利用することで合成抵抗を得ることができます。以下のように回路全体の合成抵抗\(R’\)を計算しましょう。
\(\displaystyle\frac{1}{R’}=\displaystyle\frac{1}{R_1+R_3}+\displaystyle\frac{1}{R_2+R}\)
\(\displaystyle\frac{1}{R’}=\displaystyle\frac{R_1+R_2+R_3+R}{(R_1+R_3)(R_2+R)}\)
\(R’=\displaystyle\frac{(R_1+R_3)(R_2+R)}{R_1+R_2+R_3+R}\)
こうして、全体の合成抵抗\(R’\)の計算が可能です。
検流計に電気が流れている場合の回路と合成抵抗
一方で検流計に電流が流れている場合はどのように考えればいいのでしょうか。検流計による内部抵抗が存在するのかどうかによって計算方法は異なります。なお、検流計の内部抵抗を考慮すると計算が複雑になるため、検流計による内部抵抗が存在しないと考えて解説していきます。
まず、以下のように検流計に電流\(I_3\)が流れている場面を考えましょう。

このとき前提によって内部抵抗は0であるため、オームの法則より、検流計の両端では電位差が0になります。
\(V=0×I_3=0\)
検流計の両端では電位差が0であるため、抵抗\(R_1\)と抵抗\(R_2\)に加わる電位差は同じです。電位差が同じ場合、並列接続とみなすことができます。同様に、抵抗\(R_3\)と抵抗\(R\)に加わる電位差は同じであるため、並列接続とみなせます。
そこで、以下のように図を変更しましょう。
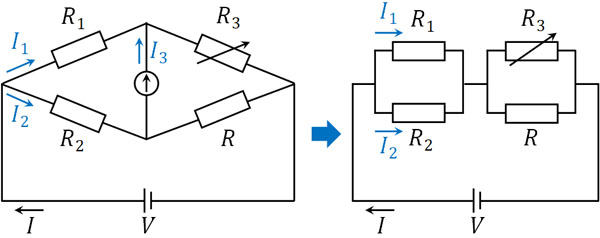
そこで、この回路を利用して合成抵抗を計算しましょう。それぞれの並列接続について、合成抵抗は以下のようになります。
・抵抗\(R_1\)と抵抗\(R_2\)の合成抵抗\(R_{12}\)
\(\displaystyle\frac{1}{R_{12}}=\displaystyle\frac{1}{R_1}+\displaystyle\frac{1}{R_2}\)
\(\displaystyle\frac{1}{R_{12}}=\displaystyle\frac{R_1+R_2}{R_1R_2}\)
\(R_{12}=\displaystyle\frac{R_1R_2}{R_1+R_2}\)
・抵抗\(R_3\)と抵抗\(R\)の合成抵抗\(R_{3R}\)
\(\displaystyle\frac{1}{R_{3R}}=\displaystyle\frac{1}{R_3}+\displaystyle\frac{1}{R}\)
\(\displaystyle\frac{1}{R_{3R}}=\displaystyle\frac{R_3+R}{R_3R}\)
\(R_{3R}=\displaystyle\frac{R_3R}{R_3+R}\)
なお\(R_{12}=\displaystyle\frac{R_1R_2}{R_1+R_2}\)と\(R_{3R}=\displaystyle\frac{R_3R}{R_3+R}\)が直列接続しているため、足すことによって全体の合成抵抗\(R’\)を得ることができます。
\(R’=\displaystyle\frac{R_1R_2}{R_1+R_2}+\displaystyle\frac{R_3R}{R_3+R}\)
こうして、検流計に電流が流れている場合の合成抵抗を計算できます。
ホイートストンブリッジの原理と計算方法を学ぶ
平衡状態のとき、ホイートストンブリッジ回路では検流計に電流が流れていません。このとき、未知の抵抗を計算によって得ることができます。
電流計や電圧計を利用することによっても抵抗を計算できます。ただ電流計や電圧計を利用する場合、内部抵抗を考慮しなければいけません。そのため内部抵抗を考慮しなくてもいいホイートストンブリッジ回路を利用すれば、正確な値を測定できます。
また合成抵抗を計算したり、検流計に電気が流れている場合の回路の計算方法を学んだりしましょう。公式を覚えてもこれらの応用問題を解くことはできないため、ホイートストンブリッジ回路の原理や概念を知る必要があります。
電流が流れない状態(平衡状態)では、電位差がありません。また回路ではキルヒホッフの法則を利用できます。これらを利用して、公式を作れるようになりましょう。






