電池を利用する場合、起電力を生じます。起電力によって電位差(電圧)が発生し、電流が流れます。このとき、起電力と電位差の違いを学びましょう。
なお、オームの法則を利用する場合は電源の起電力を利用して式を作るケースが多いです。ただ場合によっては、電池内で発生する抵抗を考慮しなければいけないケースがあります。電池内で発生する抵抗を内部抵抗といいます。
内部抵抗を考慮する場合、起電力から内部抵抗を引きましょう。これにより、電池によって発生する電位差の計算が可能です。
それでは、内部抵抗の計算はどのようにすればいいのでしょうか。電池の起電力と内部抵抗について解説していきます。
もくじ
電池の起電力とオームの法則での電位差(電圧)の違い
物理では、電位差と電圧は同じ意味です。またオームの法則での電位差(電圧)というのは、回路全体の合計電位差ではありません。一つの抵抗に加わる電圧(電圧降下の大きさ)がオームの法則で利用される\(V\)です。
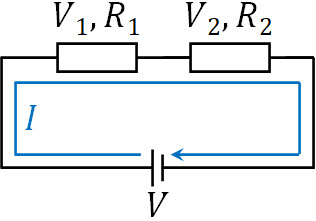
例えば以下の図であれば、\(V_1=R_1I\)であり、\(V_2=R_2I\)です。抵抗\(R_1\)の電位差は\(V_1\)であり、抵抗\(R_2\)の電位差は\(V_2\)です。
なお電気が流れるためには、電源を利用することで、元となる電位差(電圧)を作らなければいけません。
そこで電池を利用することにより、元となる電位差を発生させます。電気に高さを持たせる必要があり、先ほどの図では、合計の電位差\(V\)は\(V_1+V_2\)です。このとき、元となる電位差\(V\)(\(V_1+V_2\))を起電力といいます。
電池内部の抵抗:起電力と端子電圧の関係
なお、起電力についてより正確に学びましょう。先ほどの説明では、「起電力=抵抗に加わる電位差の合計」となります。物理で電気を学ぶとき、このような認識であっても特に大きな問題は起こりません。
ただより厳密に考えると、電池で発生するオリジナルの電位差というのは、抵抗に加わっている電位差の合計とはなりません。電池内部にも抵抗が存在し、これを内部抵抗といいます。以下のように、電池内では「起電力を発生させる部分の直後に抵抗が存在する」と理解しましょう。
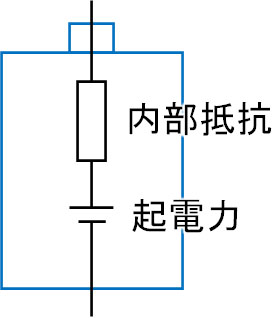
そのため厳密には、抵抗に加わる電位差を合計しても、起電力にはなりません。内部抵抗の分だけ、電位差が減少するからです。
起電力というのは、電池がもつオリジナルの電位差(高さ)を指します。ただ電流が流れると、電池の内部抵抗によって本来の電位差よりも減少します。つまり実際の電池の出力というのは、起電力から内部抵抗を差し引かなければいけません。
実際の出力を端子電圧といいます。端子電圧では、内部抵抗の分だけ起電力よりも電圧が低くなります。
電池の起電力\(E\)と内部抵抗\(r\)を利用する公式
内部抵抗がない場合、電源の起電力\(E\)と端子電圧\(V\)は同じです。ただ内部抵抗を考慮する場合、起電力\(E\)と端子電圧\(V\)を区別しましょう。
それでは、どのように内部抵抗を考慮して端子電圧\(V\)を計算すればいいのでしょうか。電流を\(I\)[A]、内部抵抗を\(r\)[Ω]とすると、オームの法則より、内部抵抗による電圧降下は\(rI\)です。そのため起電力が\(E\)[V]の場合、以下の式によって端子電圧\(V\)を計算できます。
- \(V=E-rI\)
起電力\(E\)[V]から内部抵抗による電圧降下\(rI\)[V]を引けばいいため、端子電圧\(V\)を得る公式を覚える必要はありません。内部抵抗と端子電圧が何を意味しているのか理解すれば、公式を作ることができます。
\(V=E-rI\)によるグラフの意味と電圧降下
それでは、\(V=E-rI\)は何を意味しているのでしょうか。電池に存在する内部抵抗\(r\)に変化はなく、\(r\)を定数と考えることができます。また、電池の起電力\(E\)も一定です。
一方、電流\(I\)は変化します。そこでたて軸を端子電圧\(V\)、横軸を回路に流れる電流\(I\)にしてグラフを作りましょう。以下のようになります。

このように、一次関数となります。つまり電流\(I\)の値が大きくなるほど内部抵抗による電圧降下が大きくなり、端子電圧\(V\)は小さくなります。
物理で電気を学ぶとき、前述の通り内部抵抗を無視することがほとんどです。そのため、起電力を端子電圧とみなして計算します。ただ内部抵抗を考慮する必要がある場合、内部抵抗による電圧降下を起電力から引きましょう。
電流計に内部抵抗が存在する場合の練習問題
それでは、内部抵抗に関する練習問題を解いてみましょう。内部抵抗は電池だけでなく、電流計や電圧計にも存在します。そこで、電流計または電圧計に内部抵抗が存在するケースでの電流と電圧を計算しましょう。
まずは、電流計に内部抵抗が存在する場合の問題を解きましょう。以下の問題の答えは何でしょうか。
- 電源による電流を測定するため、下図のように電流計を直列でつなぎました。電源の電圧が\(V\)、抵抗が\(R\)、電流計の内部抵抗が\(r_A\)のとき、電流計が示す値を求めましょう。なお、電源の内部抵抗は無視できます。
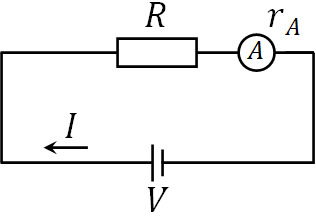
電源の内部抵抗は無視できるため、電流計の内部抵抗のみ考えましょう。この場合、抵抗2つが直列接続しているとみなせます。そのため、以下の式を作れます。
\(V=RI+r_AI\)
\(V=I(R+r_A)\)
\(I=\displaystyle\frac{V}{R+r_A}\)
こうして、電流計が示す値は\(I=\displaystyle\frac{V}{R+r_A}\)とわかります。また計算結果より、電流計の内部抵抗\(r_A\)が小さいほど、誤差が小さいとわかります。
電圧計を利用する場合の内部抵抗
次に電圧計を利用する場合の内部抵抗に関する問題を解きましょう。以下の問題の答えは何でしょうか。
- 電圧を測定するため、下図のように電圧計を並列でつなぎました。電源の電圧が\(V\)、抵抗が\(R\)、電圧計の内部抵抗が\(r_V\)のとき、電圧計が示す値を求めましょう。なお、電源の内部抵抗は無視できます。
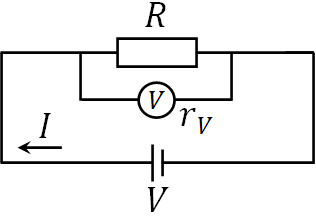
この場合、並列接続で抵抗\(R\)と抵抗\(r_V\)が存在すると考えて計算しましょう。直列接続であれば、合成抵抗は足し算をすればいいです。一方で並列接続では、逆数の足し算を利用することで計算します。合成抵抗を\(R’\)とすると、以下のように計算できます。
\(\displaystyle\frac{1}{R’}=\displaystyle\frac{1}{R}+\displaystyle\frac{1}{r_V}\)
\(\displaystyle\frac{1}{R’}=\displaystyle\frac{R+r_V}{R·r_V}\)
\(R’=\displaystyle\frac{R·r_V}{R+r_V}\)
合成抵抗がわかったため、オームの法則を利用して計算しましょう。
\(V=\displaystyle\frac{R·r_V}{R+r_V}I\)
こうして、電圧計が示す値は\(V=\displaystyle\frac{R·r_V}{R+r_V}I\)と計算できました。
・内部抵抗\(r_V\)が大きいと電圧計の精度が高い
それでは、\(V=\displaystyle\frac{R·r_V}{R+r_V}I\)から考察できることとして何があるでしょうか。電流計とは異なり、電圧計では内部抵抗\(r_V\)が大きいほど測定の精度がよくなります。なぜ、内部抵抗が大きいほど精度が高くなるのか計算によって証明してみましょう。
電圧計の値が正確な場合、\(V=RI\)となります。それでは先ほど得た式について、\(r_V\)の値を無限大に大きくしてみましょう。この場合、以下のように式を作れます。
\(V=\displaystyle \lim_{ r_V \to \infty } \displaystyle\frac{R·r_V}{R+r_V}I\)
\(V=\displaystyle \lim_{ r_V \to \infty } \displaystyle\frac{R}{\displaystyle\frac{R}{r_V}+1}I\)
\(V=RI\)
こうして、\(r_V\)の値が無限大に大きい場合、\(V=RI\)になると計算できました。
なお、この理由については計算できなくても理解できます。もし電圧計の内部抵抗が低い場合、並列接続しているため、電圧計に多くの電流が流れます。一方で電圧計の内部抵抗が大きい場合、電圧計に流れる電流は少しであり、誤差は少なくなります。そのため、電圧計の内部抵抗は大きいほど優れています。
起電力と内部抵抗の概念を学ぶ
電源を利用することによって起電力を発生させると、電流が流れます。多くの場合、起電力と電位差は意味が同じです。
ただ厳密には、起電力と電位差は異なります。起電力に対して内部抵抗による電圧降下を考慮すると、端子電圧を得ることができます。電池などの電源を利用するとき、端子電圧が回路全体の電位差と考えることができます。
そこで電池による電圧を厳密に計算したい倍、内部抵抗を利用して電圧を得られるようになりましょう。
内部抵抗の概念は簡単です。公式を覚える必要もありません。ただ計算方法を知っておく必要があり、起電力と内部抵抗を利用して電位差を得ましょう。






